Aufgabe 1 
Im Applet ist der Graph der Wurzelfunktion 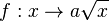 mit mit  dargestellt. dargestellt.
Variiere mit dem Schieberegler den Wert von a.
Wie ändert sich der Graph der Wurzelfunktion  für für
- a = -1
- 0 < a < 1
- 1 < a
- a < 0
|
[Lösung anzeigen][Lösung ausblenden]
- Für a = -1 wird der Graph der Wurzelfunktion
 an der x-Achse gespiegelt.
an der x-Achse gespiegelt.
- Für 0 < a < 1 wird der Graph der Wurzelfunktion
 in y-Richtung gestaucht.
in y-Richtung gestaucht.
- Für 1 < a wir der Graph der Wurzelfunktion
 in y-Richtung gestreckt.
in y-Richtung gestreckt.
- Für negative a wird der Graph von 2. oder 3. an der y-Achse gespiegelt.
Aufgabe 2 
Gib die Funktion, die jeder Oberfläche eines Würfels die Kantenlänge zuordnet als Funktionsterm an.
- Bestimme zuerst einen Term für Oberfläche O eines Würfels in Abhängigkeit der Kantenlänge a.
- Löse den Term nach a auf.
- Bestimme a für O = 24; 54; 96; 150; 216; ...
- Bestimme a für O = 108
|
[Lösung anzeigen][Lösung ausblenden]
Aufgabe 3 
Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann man bei guten Bedingungen durch die Formel 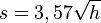 (vgl. Sichtweite) beschreiben. Dabei ist h die Augenhöhe in m und s die Sichtweite in km. Dabei geht man am besten von der Sichtweite auf dem Meer aus, da dort keine Berge stören. Ansonsten nimmt man die Kugelgestalt der Erde ohne Berge. (vgl. Sichtweite) beschreiben. Dabei ist h die Augenhöhe in m und s die Sichtweite in km. Dabei geht man am besten von der Sichtweite auf dem Meer aus, da dort keine Berge stören. Ansonsten nimmt man die Kugelgestalt der Erde ohne Berge.
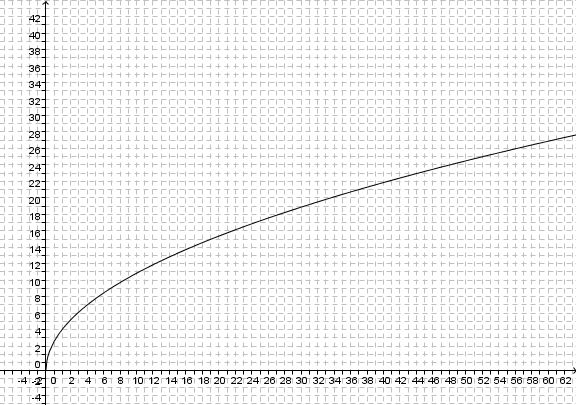
- Zeichne den Graphen zur Funktion
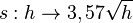 . .
- Wie weit kann man bei einer Augenhöhe von 1,7m bei klarem Wetter sehen. Löse graphisch und rechnerisch.
- Wie weit kann man von der obersten Plattform des Eiffelturms (276m), vom Mount Everest (8848m), von der ISS (380km) sehen?
- Wie hoch muss ein Berg sein, damit man 100km weit sehen kann?
|
[Lösung anzeigen][Lösung ausblenden]
-
- 4,65km
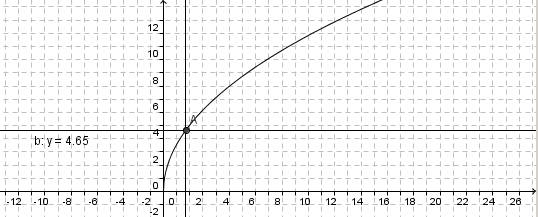
- 59,3km, 335,8km, 2200km
- 786m
Der Knorkator stellt diese Thematik musikalisch dar:
 an der x-Achse gespiegelt.
an der x-Achse gespiegelt.
 in y-Richtung gestaucht.
in y-Richtung gestaucht.
 in y-Richtung gestreckt.
in y-Richtung gestreckt.
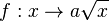 mit
mit  dargestellt.
dargestellt.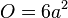
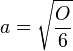
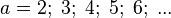
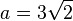
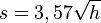 (vgl.
(vgl. 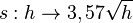 .
.



