Rationale Funktionen Indirekte Proportionalitaet
Eine Tafel Schokolade mit 24 Stücken soll auf Kinder verteilt werden. Wie viele Stückchen bekommt jedes Kind?
x bezeichne die Anzahl der Kinder und y die Anzahl der Schokoladenstückchen, die jedes Kind bekommt.
|
a) Vervollständige die Tabelle: http://wikis.zum.de/rsg/images/6/67/Tab-24-x.jpg b) Zeichne den Graph für dieses Beispiel. |
Betrachte die Produkte x*y, so stellst du fest, dass x*y= 24 ist.
|
|
In diesem Beispiel ist x eine natürliche Zahl zwischen 1 und 24.
Man kann die Funktion http://wikis.zum.de/rsg/images/0/05/F24-x.jpg allgemein für alle rationalen Zahlen x, die ungleich Null sind, erklären.
Der Graph dieser Funktion schaut dann so aus:
|
Die Funktion http://wikis.zum.de/rsg/images/a/a6/Fm_x_term.jpg mit einer rationalen Zahl m heißt indirekte Proportionalität oder indirekt proportionale Funktion. |
|
Bestimme die Definitionsmenge und die Wertemenge. Ist der Graph symmetrisch bezüglich des Koordinatensystems? |
Da x im Nenner steht, darf x nicht 0 sein, also ist die Definitionsmenge 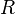 \{
\{ }.
}.
Eine solche Stelle, an der der Funktionsterm nicht definiert ist und in deren Nähe die Funktionswerte nach + Unendlich oder - Unendlich gehen, heißt Polstelle.
Aus dem Graph sieht man, dass 0 als Funktionswert nicht angenommen wird, ansonsten kommen alle reelle Zahlen als y-Werte vor, also ist die Wertemenge auch 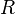 \{
\{ }.
}.
{{Arbeiten|NUMMER = 3| ARBEIT= a) Stelle in diesem Applet
den Schieberegler für m so ein, dass es den Graphen von http://wikis.zum.de/rsg/images/6/64/F24-x-graph.jpg zeigt.
2. Beantworte die Fragen auf dieser Seite
Der Funktionsterm von http://wikis.zum.de/rsg/images/0/05/F24-x.jpg ist ein Bruch, in dessen Nenner die Variable  vorkommt.
vorkommt.
Mehr über indirekte Proportionalität findest du in diesem Lernpfad.

