Einfluss der Parameter
Einfluss der Parameter
Wiederholung:
Hefteintrag: Am besten verwendest du hierfür dein Heft im Querformat. Formuliere eine Überschrift und übernehme alle mit gelb gekennzeichneten Texte. Natürlich darfst du dir aber auch noch zusätzlich Notizen machen.
|
Merke:
Die allgemeine Sinusfunktion lautet
Entsprechend lautet die allgemeine Kosinusfunktion
Dabei sind |
 Hinweis: Bei den GeoGebra-Applets ist die
Hinweis: Bei den GeoGebra-Applets ist die 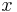 -Achse mit Vielfachen von
-Achse mit Vielfachen von 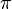 beschriftet. Indem man die
beschriftet. Indem man die 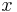 -Achse mit der rechten Maustaste anklickt und "Eigenschaften" wählt, kann man auf die Einheit cm umstellen.
-Achse mit der rechten Maustaste anklickt und "Eigenschaften" wählt, kann man auf die Einheit cm umstellen.
Arbeiten in Expertenteams
Einfluss von 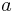 |
Einfluss von 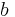 |
Einfluss von  |
Einfluss von 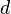
|
|---|---|---|---|
|
Untersuche hier den Einfluss von auf die Graphen der Funktionen und
|
Untersuche hier den Einfluss von auf die Graphen der Funktionen und
|
Untersuche hier den Einfluss von auf die Graphen der Funktionen und
|
Untersuche hier den Einfluss von auf die Graphen der Funktionen und
|
Arbeiten in Expertenteams
Sinus und Kosinus
|
Wie hängen die Sinus- und die Kosinusfunktion zusammen? Erstelle die Graphen
der Funktionen |
Lösung:
Ja genau, die Graphen der beiden Funktionen sind identisch. Genauer gesagt:
|
Merke:
Man erhält den Graphen der Kosinusfunktion indem man den Graphen der Sinusfunktion um Deshalb verhält sich die allgemeine Kosinusfunktion bei Variation ihrer Parameter genauso wie die allgemeine Sinusfunktion. |
Jetzt noch was zum Knobeln!!!
Du hast eine Menge über den Einfluss der einzelnen Parameter auf das Aussehen der Graphen heraus gefunden. Natürlich können aber die Parameter nicht nur einzeln variiert werden, sondern auch mehrere oder alle gleichzeitig.
|

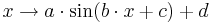
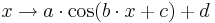
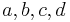 Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Im Folgenden seien
Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Im Folgenden seien 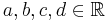 und
und 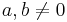 .
.
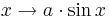
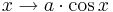 .
.
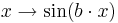
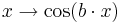 .
.
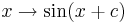
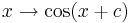 .
.
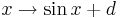
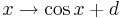 .
.
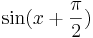 und
und 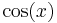 und
betrachte sie! Was fällt dir auf?
und
betrachte sie! Was fällt dir auf?
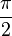 nach links verschiebt.
nach links verschiebt.

