Quadratische Funktionen - Bremsweg
Einführung - Bremsweg - Unterschiedliche Straßenverhältnisse - Übungen 1 - Anhalteweg - Übungen 2 - Stationenbetrieb - Allgemeine quadratische Funktion - Übungen 3
Einstieg
Eine gute Bremsung ist für unsere eigene Sicherheit und die der anderen Verkehrsteilnehmer sehr wichtig. Folgendes Video ist leider kein Beleg für die Aussage!=)
Schlechter Bremsweg
So nun aber zum Ernst zurück... Oftmals stellt sich die Frage:
Ist bei doppelter Geschwindigkeit auch der Bremsweg doppelt so lang? Was meinst du?
Diese Frage wurde im Fernsehen bei Kopfball.de untersucht. In dem Video aus der Sendung findest du eine Antwort!!
Tabelle, Graph und Formel
Die Polizei hat Messungen durchgeführt, um den Zusammenhang zwischen der Geschwindigkeit eines Autos und seinem Bremsweg zu erkunden. Klar ist: Je schneller eine Auto fährt, desto länger ist sein Bremsweg. Aber ist das wirklich so einfach...?
Du kannst den Zusammenhang selbst untersuchen. Hier sind die Daten, die die Polizei gesammelt hat:
Geschwindigkeit (in km/h) 10 20 30 40 50 80 100 120 Bremsweg (in m) 1 4 9 16 25 64 100 144
|
|
|
In Tests wird die Güte von Bremsanlagen getestet. Dazu wird eine Vollbremsung aus einer Geschwindigkeit von 100km/h durchgeführt. Sehr gute Bremsanlagen bringen das Auto auf trockener Straße nach 36m zum Stillstand. Bei ungünstigen Straßenverhältnissen beträgt der Bremsweg 60m . |
- Um wie viel Prozent ist der Bremsweg bei ungünstigen Verhältnissen höher als der auf einer trockenen Straße?
- Wie verändert sich der Bremsweg allgemein, wenn die Geschwindigkeit eines Autos verdoppelt bzw. halbiert wird?
- Die Länge des Bremsweges kann in Abhängigkeit von der gefahrenen Geschwindigkeit durch eine Funktionsgleichung der Form s(v) = k·v² beschrieben werden. Bestimme die Konstante k für beide Straßenverhältnisse.
- In Wohngebieten gibt es oft eine Geschwindigkeitsbegrenzung auf 30km/h . Wie lang sind die Bremswege bei dieser Geschwindigkeit? Vergleiche mit den Bremswegen bei der sonst in der Stadt üblichen Geschwindigkeit von 50km/h . Beurteile den Sinn von Geschwindigkeitsbegrenzungen in Wohngebieten.
Schreibe dir nun die neuen Erkenntnisse, die du in diesem Kapitel erworben hast auf und versuche sie auch mit Hilfe deines Partners zu verstehen! Was ist an Stoff neu hinzugekommen, was war bereits bekannt? Mache dir Gedanken.
Lösung zur Aufgabe1:
Lösung zur Aufgabe 2:
Lösung zur Aufgabe 3:

|
Als nächstes erfährst du, wie die Länge des Bremsweges von der "Bremsbeschleunigung" abhängig ist. |

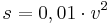 oder
oder 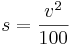 (dabei ist s der Bremsweg in Metern und v die Geschwindigkeit in km/h)
(dabei ist s der Bremsweg in Metern und v die Geschwindigkeit in km/h)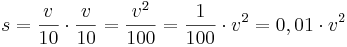 . Die Formeln stimmen also überein.
. Die Formeln stimmen also überein.
