Quadratische Funktionen - Übungen3

Einführung - Bremsweg - Unterschiedliche Straßenverhältnisse - Übungen 1 - Anhalteweg - Übungen 2 - Stationenbetrieb - Allgemeine quadratische Funktion - Übungen 3

Falls es Probleme mit der Ansicht gibt, bitte Firefox als Browser verwenden!

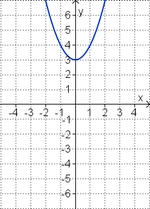
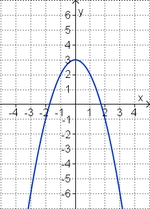
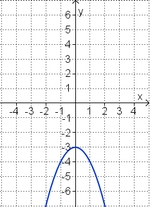
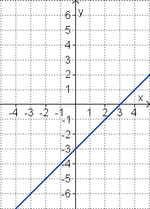
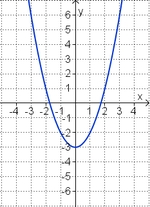
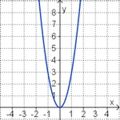
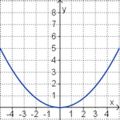
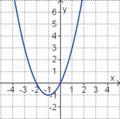
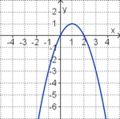
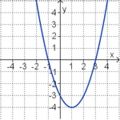
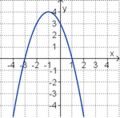
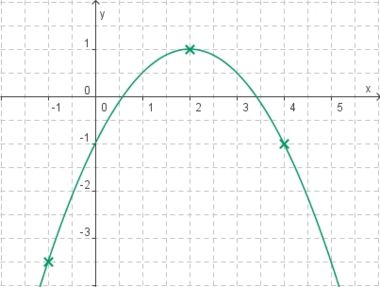
Aufgabe 1: Funktionsterm finden Die Parabel hat die Funktionsgleichung f(x) = ax2 + bx + c. Welcher Funktionsterm passt? (-0,5x2 + 2x - 1) (!0,5x2 - 2x + 3) (!-2x2 + 8x - 7) (!-0,5x2 + 2x + 1) (!0,5x2 - 2x - 1) Aufgabe 2: Term und Graph zuordnen Ordne den Funktionsgraphen den richtigen Term zu. x2 + 3 -x2 + 3 -x + 3 -x2 - 3 x - 3 x2 - 3 Aufgabe 3: Multiple Choice Kreuze jeweils alle richtigen Aussagen an. f(x) = –2x2 + 3x – 4 (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|-6] liegt auf dem Graphen.) (Der Punkt [1|1] liegt nicht auf dem Graphen.) Welche Terme gehören zu einer Funktion, deren Graph symmetrisch zur y-Achse ist? (7x2) (7x2 - 2) (7x2 + 3) (!7x2 - 2x) (!7x2 + 3x) (!7x2 - 2x + 3) Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der y-Achse symmetrisch zueinander sind? (!7x2 und -7x2) (7x2 - 2x und 7x2 + 2x) (!7x2 - 2x und -7x2 + 2x) (!7x2 - 2 und 7x2 + 2) (-7x2 + 2x und -7x2 - 2x) Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der x-Achse symmetrisch zueinander sind? (7x2 und -7x2) (!7x2 - 2x und 7x2 + 2x) (!7x2 - 2 und 7x2 + 2) (7x2 - 2 und -7x2 + 2) (!7x2 - 2 und -7x2 + 2x) Aufgabe 4: Memo-Quiz Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion (Öffnung der Parabel, Lage des Scheitels, Nullstellen). f(x) = x2 + 3 f(x) = -x2 + 3 f(x) = 3x2 f(x) = 0,2x2 f(x) = x2 + 2x f(x) = –x2 + 2x f(x) = x2 – 2x – 3 f(x) = –x2 – 2x + 3 Aufgabe 5: Verschiebung und Streckung Eine Parabel der Form ax²+bx+c wird a) in y- Richtung verschoben und b) in y- Richtung gestreckt. Welche Eigenschaften der Parabel bleiben erhalten, welche ändern sich? (Hinweis: Diskutiere mit deinem Partner und zeichne dir zur Hilfe eine Parabel auf und verschiebe bzw. strecke sie!) [Lösung anzeigen][Lösung ausblenden] a) Verschiebung in y- Richtung: Die Form bleibt erhalten, der y- Wert des Scheitels ändert sich. Die Achsenschnittpunkte ändern sich. 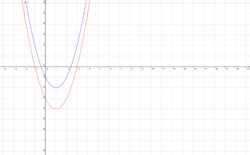f(x) ist die blaue Funktion, g(x) stellt die rote, in y- Richtung verschobene Funktion dar. b) Streckung in y- Richtung: Schnittpunkte mit der x- Achse bleiben unverändert. Die Form und der y- Wert des Scheitelpunktes ändert sich. Schnittpunkt mit der y- Achse ändert sich. 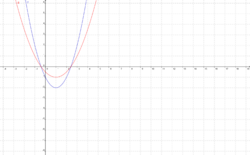f(x) ist die blaue Funktion, g(x) stellt die rote, in y- Richtung gestreckte Funktion dar. Dieser Lernpfad wurde erstellt von: Reinhard Schmidt, Christian Schmidt, Maria Eirich, Andrea Schellmann