Quadratische Funktionen 2 Einfluss von b
Aus Medienvielfalt-Wiki
Version vom 13. Juli 2011, 17:02 Uhr von Karlo Haberl (Diskussion | Beiträge)
|
Wir betrachten nun den Einfluss von
|
|
Aufgabe 1:
Man erhält den Graph der Funktion 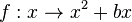
aus dem Graph der Quadratfunktion 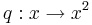 durch Verschiebung sowohl in x- wie auch in y-Richtung
durch Verschiebung sowohl in x- wie auch in y-Richtung
Genauer:
- Ist b > 0, so wird die Normalparabel schräg nach links unten verschoben.
- Ist b < 0, so wird die Normalparabel schräg nach recht unten verschoben.
- Je größer der Betrag von B ist, desto mehr wird in y-Richtung verschoben
- Der Graph zu -b ist spiegelsymmetrisch zur y-Achse zum Graph von b.
Aufgabe 2:
Zum Graph der Quadratfunktion 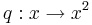 , der Normalparabel, wird noch die Gerade y = bx addiert. Daher kommt für positives B im III.Quadrant ein negativer und im I. Quadrant ein positiver Anteil, für negatives B im II.Quadrant ein positiver und im IV. Quadrant ein negativer Anteil dazu. Dies bewirkt eine Verschiebung des Scheitels. Ansonsten hat der Graph weiterhin das Aussehen einer Normalparabel.
, der Normalparabel, wird noch die Gerade y = bx addiert. Daher kommt für positives B im III.Quadrant ein negativer und im I. Quadrant ein positiver Anteil, für negatives B im II.Quadrant ein positiver und im IV. Quadrant ein negativer Anteil dazu. Dies bewirkt eine Verschiebung des Scheitels. Ansonsten hat der Graph weiterhin das Aussehen einer Normalparabel.
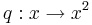 , der Normalparabel, wird noch die Gerade y = bx addiert. Daher kommt für positives B im III.Quadrant ein negativer und im I. Quadrant ein positiver Anteil, für negatives B im II.Quadrant ein positiver und im IV. Quadrant ein negativer Anteil dazu. Dies bewirkt eine Verschiebung des Scheitels. Ansonsten hat der Graph weiterhin das Aussehen einer Normalparabel.
, der Normalparabel, wird noch die Gerade y = bx addiert. Daher kommt für positives B im III.Quadrant ein negativer und im I. Quadrant ein positiver Anteil, für negatives B im II.Quadrant ein positiver und im IV. Quadrant ein negativer Anteil dazu. Dies bewirkt eine Verschiebung des Scheitels. Ansonsten hat der Graph weiterhin das Aussehen einer Normalparabel.
Hefteintrag: Beachte, dass in der Lösung zur Aufgabe A1 ein Hefteintrag "versteckt" ist!
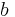 in
in 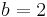 ein. Wie ändert sich der Graph?
ein. Wie ändert sich der Graph? 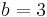 und
und 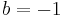 sowie
sowie 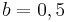 auf den Graphen auswirken und überprüfe deine Vermutung.
auf den Graphen auswirken und überprüfe deine Vermutung. 
