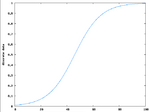
Diskret - kontinuierlich

Willkommen zum Lernpfad

Diskret - kontinuierlich

erstellt von

Matthias Kittel und Walter Wegscheider

im Rahmen eines internationalen Projektes von
Medienvielfalt im Mathematikunterricht
(Stand August 2011)

Du erwirbst / stärkst in diesem Lernpfad folgende Kompetenzen  [Anzeigen][Verstecken]

Das kennst Du schon

• Darstellungsformen von Funktionen
• Kenntnis der Auswirkung von Variationen in verschiedenen Darstellungsformen (lineare, quadratische Funktionen, Potenzfunktionen, trigonometrische Funktionen u.a.)

Das lernst Du

• Wie beschreibt man diskrete dynamische Vorgänge mit Hilfe von Differenzengleichungen - Lösungsmöglichkeiten und Visualisierung an verschiedenen Beispielen
• Wie beschreibt man kontinuierliche dynamische Vorgänge mit Hilfe von Differentialgleichungen - Visualisierung und Lösungsansätze mit Hilfe verschiedener Technologieunterstützungen an verschiedenen Beispiele

Du stärkst diese Kompetenzen:

• Darstellen, Modellieren (Heronverfahren, Radioaktiver Zerfall, Räuber-Beute-Modell, Rekursionsmodelle und Differenzengleichungen Differentialgleichung)
• Rechnen, Operieren (Radioaktiver Zerfall - analytische Herleitung sowie weiterführende Aufgaben, Herleitung der logistischen Gleichung, Lösen von Differentialgleichungen)
• Interpretieren (exponentielles Wachstum - Lebensmittelkontrolle, exponentielle Abnahme - radioaktiver Zerfall)
• Argumentieren, Begründen (Unterschied zwischen Differenzen- und Differentialgleichung)n
• Problemlösen (Erkennen der Einsatzgebiete von Differenzen- und Differentialgleichung)

Informationen zum Einsatz des Lernpfads im Unterricht: Didaktischer Kommentar

Differentialgleichungen

Begriffsbildung

Als (gewöhnliche) DGLG wird eine Gleichung bezeichnet, die neben einer Unbekannten 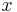$\,x$ auch deren Ableitung(en) 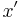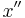$\,x'$ ($\,x''$, ...) enthält. Gelöst wird eine DGLG mittels Integralrechnung.

Die Lösung einer DGLG ist nicht wie bei einer herkömmlichen Gleichung eine Zahl, sondern eine Funktion, genauer eine Funktionenschar, die aus unendlich vielen Funktionen besteht. Da beim unbestimmten Integrieren immer eine Integrationskonstante auftritt, muss eine Zusatzinformation (Anfangsbedingung) gegeben sein, um die Konstante zu bestimmen.

Erst durch die Anfangsbedingung, die einem Punkt auf dem Graphen der Lösungsfunktion entspricht, kann die Lösungsfunktion exakt bestimmt werden. Die Lösung ist nun eine spezielle Funktion!

DGLG können in allen Bereichen des Lebens angetroffen werden, besonders in den Naturwissenschaften oder der Wirtschaft und dem Sport. In allen Zusammenhängen, bei denenen es um Veränderungen geht, kommen DGLG zur Anwendung.

Eine Übersicht über die Klassifikation von DGLG findet man unter Einteilung von Differentialgleichungen, T. Wolf, Fachhochschule Landshut (pdf-Datei, 14 kB)

Links:

• Differentialgleichungen, Josef Leydold, Abt. f. angewandte Statistik und Datenverarbeitung, 1997
• http://www.acdca.ac.at/material/kl8/diffequ.htm, Josef Böhm, Differentialgleichungen mit CAS, ACDCA 2004

Ausblick

Oftmals ist bei realitätsnahen Modellen nicht möglich die gegebenen Differentialgleichung(en) exakt zu lösen. Aus diesem Grund ist es zielführend manchmal Näherungsverfahren zu verwenden.

Näherungsverfahren

---

© 2009, Projekt "Medienvielfalt im Mathematikunterricht"