Graphen
Funktionen grafisch darstellen
Sehr nützlich für die Darstellung von Funktionen ist der Funktionsgraph. Abhängigkeiten zwischen Größen können so auf grafische Weise dargestellt werden. Auch diese Darstellungsform kann mathematisch genauer gefasst werden:
 |
Die graphische Darstellung von Funktionen wollen wir nun ein bisschen üben.
|
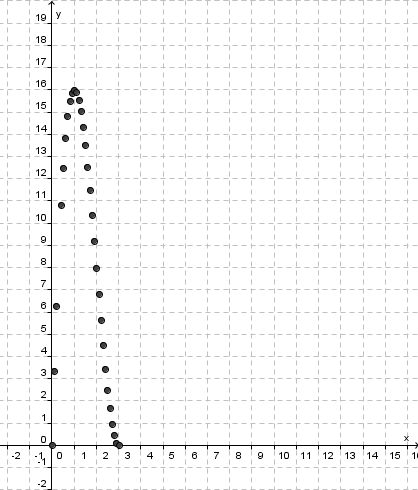
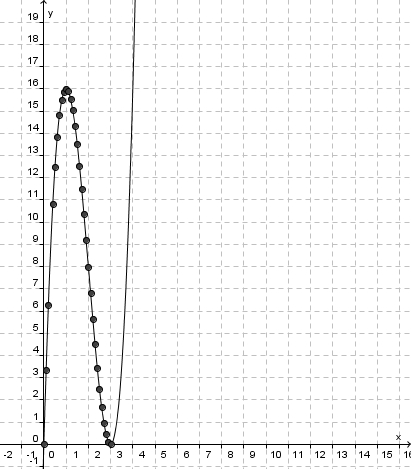
In der Aufgabe Schachtelbeispiel hast du zwei Wertetabellen für den Zusammenhang zwischen V und x erstellt.
(Tipp: Jede Zeile in einer Wertetabelle wird durch einen Punkt in der Zeichenebene dargestellt. Wähle einige beliebige Zeilen einer Wertetabelle aus und zeichne die entsprechenden Punkte in der Ebene ein! Der Graph ist die Menge aller Punkte, die du auf diese Weise einzeichnen könntest: er ist eine Kurve).
|
|
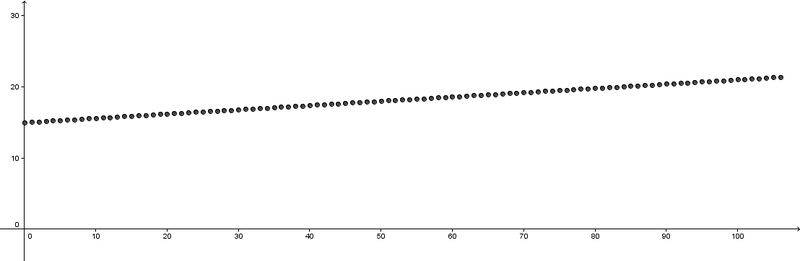
Auch der Zusammenhang zwischen der Gesprächszeit und der Höhe der Telefonrechnung kann grafisch dargestellt werden. 2. Unser Hotline-Betreuer bekommt einen neuerlichen Anruf: Irene möchte im Monat höchstens 20 € fürs Telefonieren ausgeben. Wie viele Minuten darf sie dann telefonieren? a) Benutze zuerst die von dir erstellte Grafik, um diese Frage zu beantworten! b) Danach benutze die von dir erstellte Wertetabelle, um die Frage zu beantworten! Sind die beiden Antworten gleich? (Und sind sie gleich genau?) Welche Methode fällt dir leichter? |