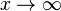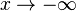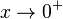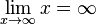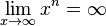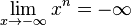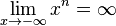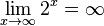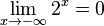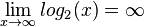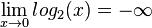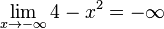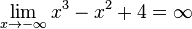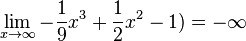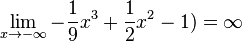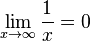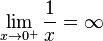Grenzwert
zurück zu Eigenschaften von Funktionen
|
Zuerst vereinbaren wir: sehr große positve Zahlen sind solche positive Zahlen mit großem Betrag (z.B. 1000000) sehr kleine positive Zahlen sind solche positive Zahlen mit kleinem Betrag (z.B. 0,0000001) Grenzwerte von Funktionen spiegeln das Verhalten im Unendlichen wieder oder, falls wir x gegen einen anderen Wert als unendlich laufen lassen, das entsprechende Verhalten. Beispiel: Wir betrachten die Funktion Wenn x gegen 3 (man schreibt Man nennt dies den Grenzwert von Wir können x auch gegen unendlich und gegen minus unendlich laufen lassen. Wir schreiben für x gegen unendlich: und für x gegen minus unendlich: Da in beiden Fällen die Funktionswerte immer größer werden und über alle Grenzen wachsen, ist dann Ein Plus-oder Minuszeichen rechts hochgestellt an einer Zahl bei Grenzwerten bedeutet Annäherung von rechts – bzw. von links her an die Zahl
Es ist dann
|
|
Verändere im folgenden Applet mit dem Schieberegler den Wert von h.
|
- h = 0
-
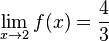
- in beiden Fällen
 , also
, also 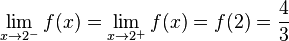
-
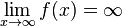
Auf den folgenden Seiten sind zum Thema Grenzwert weitere Erklärungen und Beispiele zu finden:
- Grenzwert an einer Stelle
- Beispiel mit Grenzwert und ohne Grenzwert
- Beispiele: Identische Funktion, konstante Funktion, Betragsfunktion, trigonometrische Funktionen, Potenz-, Exponential- und Logarithmusfunktionen
|
Bestimme die Grenzwerte folgender Funktionen:
|
|
Bestimme die Grenzwerte gegen
|
Falls du Hilfe brauchst, öffne GeoGebra,gib die Funktionsterme ein und betrachte den Graphen.
Links
Sehr viel mehr über Grenzwerte und ihre Handhabung, speziell für rationale Funktionen, erfährst du im Crashkurs Grenzwerte
zurück zu Eigenschaften von Funktionen
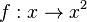
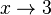 )geht, dann geht der Funktionswert gegen
)geht, dann geht der Funktionswert gegen 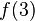 .
.
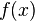 für x gegen 3 und schreibt
für x gegen 3 und schreibt 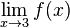 oder
oder 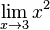 . Es ist dann
. Es ist dann 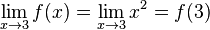
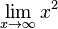
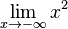
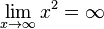 und
und 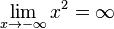
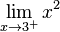 heißt: x ist bei der Annäherung größer als 3, also z.B. 3,1 ; 3,01 ; 3,001 usw.
heißt: x ist bei der Annäherung größer als 3, also z.B. 3,1 ; 3,01 ; 3,001 usw.
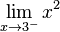 heißt: x ist bei der Annäherung kleiner als 3, also z.B. 2,9 ; 2,99 ; 2,999 usw.
heißt: x ist bei der Annäherung kleiner als 3, also z.B. 2,9 ; 2,99 ; 2,999 usw.
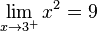 bzw.
bzw. 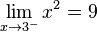 .
.
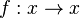 für
für 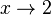
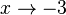
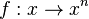 für
für 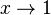
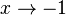 wenn n ungerade
wenn n ungerade
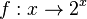 für
für 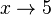
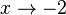
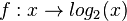 für
für 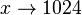
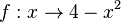 für
für 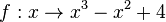 für
für 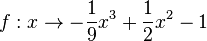 für
für 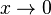
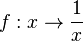 für
für 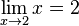
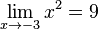
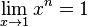
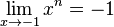
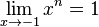
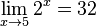
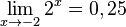
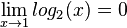
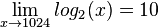
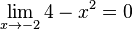
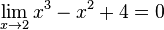
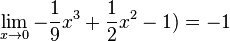
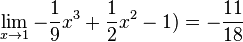
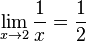
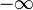 oder
oder 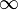 folgender Funktionen:
folgender Funktionen: