Rationale Funktionen senkrechte Asymptoten
Aus Medienvielfalt-Wiki
Version vom 5. März 2013, 20:55 Uhr von Karlo Haberl (Diskussion | Beiträge)
Die Funktion 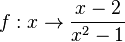 hat die Definitionslücken
hat die Definitionslücken 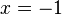 und
und 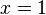 .
.
Es ist 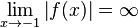 , da z(-1) = 1 ist.
, da z(-1) = 1 ist. 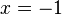 ist Polstelle und die Gerade
ist Polstelle und die Gerade 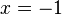 ist senkrechte Asymptote für den Graphen von f.
ist senkrechte Asymptote für den Graphen von f.
Ebenso ist 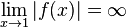 , da z(1) = 1 ist.
, da z(1) = 1 ist. 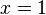 ist Polstelle und die Gerade
ist Polstelle und die Gerade 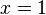 ist senkrechte Asymptote für den Graphen von f.
ist senkrechte Asymptote für den Graphen von f.
|
Ist an einer Definitionslücke
dann ist die Definitionslücke Die Gerade mit der Gleichung |
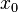 einer gebrochen-rationalen Funktion
einer gebrochen-rationalen Funktion 
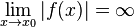 ,
,
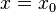 ist senkrechte Asymptote des Graphen von f.
ist senkrechte Asymptote des Graphen von f.

