Rationale Funktionen Definitionsmenge: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | Bei Zahlbrüchen hast du kennengelernt, dass der Nenner des Bruches nie <math>0</math> sein darf. Dies gilt natürlilch auch weiterhin. Bei den gebrochen-rationalen Funktionen steht natürllich keine <math>0</math> explizit im Nenner, aber es gibt Terme, die den Wert <math>0</math> annehmen können. Dies darf nicht geschehen. Daher müssen wir die x-Werte, die zum Termwert <math>0</math> im Nenner führen, ausschließen. | ||
| + | |||
| + | Die Funktion | ||
| + | |||
| + | 1. <math>f:x\rightarrow \frac{x-2}{x^2-1}</math> hat den Nennerterm <math>x^2-1</math>. Dieser Term nimmt für <math> x = -1</math> und <math> x = 1</math> den Wert <math>0</math> an. | ||
| + | |||
| + | 2. <math>f:x\rightarrow \frac{x-2}{x^2-2x+1}</math> hat den Nennerterm <math>x^2-2x+1</math>. Dieser Term nimmt für <math> x = 1</math> den Wert <math>0</math> an. | ||
| + | |||
| + | 3. <math>f:x\rightarrow \frac{x^2-2}{x^3-x^2-2x}</math> hat den Nennerterm <math>x^3-x^2-2x</math>. Dieser Term nimmt für <math> x = -1</math>, <math>x=0</math> und <math> x = 2</math> den Wert <math>0</math> an. | ||
| + | |||
{{Merke| | {{Merke| | ||
Der Nenner eines Bruches darf nie den Wert Null annehmen darf. Daher darf man für <math>x</math> keine Werte einsetzen, dass das Nennerpolynom <math>h(x) = b_nx^n+b_{n-1}x^{n-1}+ ... + b_1 x+b_0 = 0</math> ist. | Der Nenner eines Bruches darf nie den Wert Null annehmen darf. Daher darf man für <math>x</math> keine Werte einsetzen, dass das Nennerpolynom <math>h(x) = b_nx^n+b_{n-1}x^{n-1}+ ... + b_1 x+b_0 = 0</math> ist. | ||
| Zeile 7: | Zeile 17: | ||
<math> D = R</math> \ <math>\begin{Bmatrix} x & |h(x)=0 \end{Bmatrix}</math> | <math> D = R</math> \ <math>\begin{Bmatrix} x & |h(x)=0 \end{Bmatrix}</math> | ||
| − | |||
}} | }} | ||
| Zeile 21: | Zeile 30: | ||
| − | {{ | + | {{Arbeiten|NUMMER=1| |
| + | ARBEIT= | ||
Ordne die Definitionsmengen und die angegebenen Funktionen <math> f: x \rightarrow f(x)</math> richtig zu! | Ordne die Definitionsmengen und die angegebenen Funktionen <math> f: x \rightarrow f(x)</math> richtig zu! | ||
}} | }} | ||
| Zeile 37: | Zeile 47: | ||
|- | |- | ||
| <math>f(x) = \frac{x^2-2x}{x^2-64}</math> || D = R \{-8;8} | | <math>f(x) = \frac{x^2-2x}{x^2-64}</math> || D = R \{-8;8} | ||
| + | |- | ||
| + | | <math>f(x) = \frac{x^2-2x}{x^2+64}</math> || D = R | ||
|} | |} | ||
</div> | </div> | ||
| + | |||
| + | {{Arbeiten|NUMMER=2| | ||
| + | ARBEIT= | ||
| + | Gib jeweils die maximale Definitionsmenge an: | ||
| + | |||
| + | a) <math>f</math> mit <math>f(x) = \frac{13}{(x-1)^2}</math> | ||
| + | |||
| + | b) <math>g</math> mit <math>g(x) = \frac{16}{x^2+1}</math> | ||
| + | |||
| + | c) <math>h</math> mit <math>h(x) = \frac{16}{x^2-1}</math> | ||
| + | |||
| + | d) <math>k</math> mit <math>k(x) = \frac{x^2+3x+2}{(x-3)(x-2)}</math> | ||
| + | |||
| + | e) <math>l</math> mit <math>l(x) = \frac{x-2}{(x^2-5x+6)}</math> | ||
| + | |||
| + | f) <math>m</math> mit <math>m(x) = \frac{x+2}{x^2+x-6}</math> | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt|1= | ||
| + | |||
| + | a) D=R \ {1} | ||
| + | |||
| + | b) D=R | ||
| + | |||
| + | c) D=R \ {-1;1} | ||
| + | |||
| + | d) D=R \ {2;3} | ||
| + | |||
| + | e) D=R \ {2;3} | ||
| + | |||
| + | f) D=R \ {-3;2} | ||
| + | }} | ||
Aktuelle Version vom 3. April 2013, 17:28 Uhr
Bei Zahlbrüchen hast du kennengelernt, dass der Nenner des Bruches nie  sein darf. Dies gilt natürlilch auch weiterhin. Bei den gebrochen-rationalen Funktionen steht natürllich keine
sein darf. Dies gilt natürlilch auch weiterhin. Bei den gebrochen-rationalen Funktionen steht natürllich keine  explizit im Nenner, aber es gibt Terme, die den Wert
explizit im Nenner, aber es gibt Terme, die den Wert  annehmen können. Dies darf nicht geschehen. Daher müssen wir die x-Werte, die zum Termwert
annehmen können. Dies darf nicht geschehen. Daher müssen wir die x-Werte, die zum Termwert  im Nenner führen, ausschließen.
im Nenner führen, ausschließen.
Die Funktion
1. 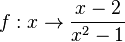 hat den Nennerterm
hat den Nennerterm 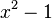 . Dieser Term nimmt für
. Dieser Term nimmt für 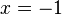 und
und 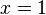 den Wert
den Wert  an.
an.
2. 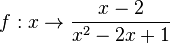 hat den Nennerterm
hat den Nennerterm 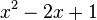 . Dieser Term nimmt für
. Dieser Term nimmt für 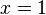 den Wert
den Wert  an.
an.
3. 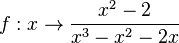 hat den Nennerterm
hat den Nennerterm 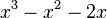 . Dieser Term nimmt für
. Dieser Term nimmt für 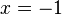 ,
,  und
und 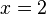 den Wert
den Wert  an.
an.
|
Der Nenner eines Bruches darf nie den Wert Null annehmen darf. Daher darf man für Die Nullstellen des Nennerpolynoms werden als Definitionslücken bezeichnet. Die Definitionsmenge der gebrochen-rationalen Funktion
|
Beispiele:
Die Funktion
1. 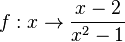 hat, da sich der Nenner
hat, da sich der Nenner 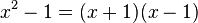 umformen lässt, die Definitionslücken
umformen lässt, die Definitionslücken 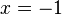 und
und 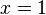 , also ist
, also ist 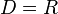 \
\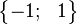 .
.
2. 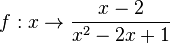 hat, da sich der Nenner
hat, da sich der Nenner 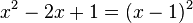 umformen lässt, die Definitionslücke
umformen lässt, die Definitionslücke 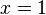 , also ist
, also ist 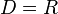 \
\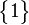 .
.
3. 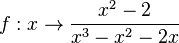 hat, da sich der Nenner
hat, da sich der Nenner 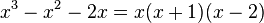 umformen lässt, die Definitionslücken
umformen lässt, die Definitionslücken 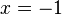 ,
,  und
und 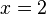 , also ist
, also ist 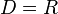 \
\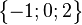 .
.
|
Ordne die Definitionsmengen und die angegebenen Funktionen |
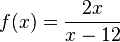 |
D = R \{12} |
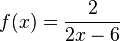 |
D = R \{3} |
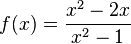 |
D = R \{-1;1} |
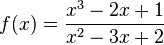 |
D = R \{1;2} |
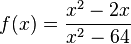 |
D = R \{-8;8} |
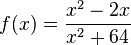 |
D = R |
|
Gib jeweils die maximale Definitionsmenge an: a) b) c) d) e) f) |
a) D=R \ {1}
b) D=R
c) D=R \ {-1;1}
d) D=R \ {2;3}
e) D=R \ {2;3}
f) D=R \ {-3;2} keine Werte einsetzen, dass das Nennerpolynom
keine Werte einsetzen, dass das Nennerpolynom 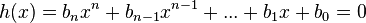 ist.
ist.
 mit
mit 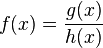 ist die Menge der reellen Zahlen ohne die Nullstellen des Nennerpolynoms h(x).
ist die Menge der reellen Zahlen ohne die Nullstellen des Nennerpolynoms h(x).
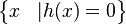
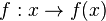 richtig zu!
richtig zu!
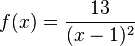
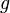 mit
mit 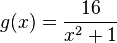
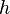 mit
mit 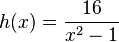
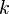 mit
mit 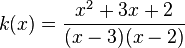
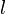 mit
mit 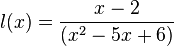
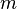 mit
mit