Der Funktionsbegriff: Unterschied zwischen den Versionen
| Zeile 62: | Zeile 62: | ||
# Definitionsmenge ist <math>R^+</math>, Zielmenge ist <math>R</math>. | # Definitionsmenge ist <math>R^+</math>, Zielmenge ist <math>R</math>. | ||
# Die unabhängige Variabel ist <math>t</math>, die abhängige Variable <math>H(t)</math>. | # Die unabhängige Variabel ist <math>t</math>, die abhängige Variable <math>H(t)</math>. | ||
| − | # <math> H(0)=15; H( | + | # <math> H(0)=15; H(15)=15,9; H(43)=17,58; H(167)=25,02</math> |
| − | + | # <math> H(0)=15; H(15)=15,99; H(43)=16,1304; H(167)=16,566</math> | |
}} | }} | ||
Version vom 21. Dezember 2011, 19:16 Uhr
In den bisherigen Aufgaben ist es darum gegangen, Abhängigkeiten
- durch eine Formel auszudrücken und
- in Tabellenform wiederzugeben
Was haben das Handybeispiel und das Schachtelbeispiel gemeinsam? In beiden Fällen haben wir Vorschriften betrachtet, die es gestatten,
einem gegebenen Objekt (z.B. die Länge der Quadratseite x) Fehler beim Parsen(Syntaxfehler): \right
ein anderes davon abhängiges Objekt (z.B. das Schachtelvolumen V(x))
zuzuordnen. Diese Idee der Zuordnung ist in der Mathematik sehr wichtig. Dabei können wir an ganz unterschiedliche Objekte (wie beispielsweise natürliche Zahlen oder reelle Zahlen) denken.
Wir wollen nun etwas genauer formulieren, wie die Idee der Zuordnung für die Mathematik nutzbar gemacht werden kann. Dazu müssen wir - wie es dem Genauigkeitsanspruch der Mathematik entspricht - für jede konkrete Zuordnung festlegen, um welche Objekte es sich dabei handelt. Wir fassen alle möglichen "gegebenen Objekte" in einer Menge A zusammen und stellen uns vor, dass alle möglichen "abhängigen Objekte" in einer Menge B liegen. So gelangen wir zur Definition des Funktionsbegriffs, wie er in der Mathematik seit mehr als 100 Jahren verwendet wird:
|
Definition: |
Bezeichnungen:
Die Menge 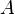 nennen wir Definitionsmenge, die Menge
nennen wir Definitionsmenge, die Menge 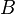 heißt Zielmenge.
heißt Zielmenge.
Wie andere mathematische Objekte auch werden Funktionen mit Symbolen (in der Regel mit Buchstaben) bezeichnet. Bezeichnen wir eine Funktion von 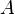 nach
nach 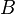 mit dem Buchstaben
mit dem Buchstaben  , so schreiben wir dafür auch
, so schreiben wir dafür auch
Fehler beim Parsen(Syntaxfehler): f : A \right B
gesprochen: " ist eine Funktion von
ist eine Funktion von 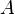 nach
nach 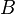 "
"
Wir sagen auch: Jedes 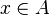 wird von der Funktion
wird von der Funktion  auf ein Element von
auf ein Element von 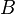 abgebildet. Dieses Element von
abgebildet. Dieses Element von 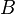 schreiben wir als
schreiben wir als 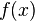 .
.
Funktionen werden manchmal auch Abbildungen genannt.
Lässt sich durch einen Term (d.h. durch eine Formel) angeben, wie 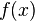 aus
aus  ermittelt wird, so sprechen wir von einer "Termdarstellung der Funktion
ermittelt wird, so sprechen wir von einer "Termdarstellung der Funktion  ". So ist beispielsweise durch die Termdarstellung
". So ist beispielsweise durch die Termdarstellung
jene Funktion definiert, die jedem Element der Definitionsmenge sein Quadrat zuordnet. Die Aussage 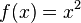 wird auch als Funktionsgleichung bezeichnet. Eine andere Schreibweise dafür ist
wird auch als Funktionsgleichung bezeichnet. Eine andere Schreibweise dafür ist
Fehler beim Parsen(Syntaxfehler): f : x \right x^2
.
Eine Termdarstellung ist eine durch einen Term ausgedrückte Zuordnungsvorschrift.
Die meisten elektronischen Rechenwerkzeuge gestatten es, eine Funktion, d.h. eine Zuordnungsvorschrift einzugeben, um sie später bei Bedarf anwenden zu können.
Bemerkung:
In vielen Anwendung der Mathematik auf reale Situationen kommen Abhängigkeiten vor, die durch Formeln beschrieben werden. Beim Aufstellen eines mathematisch strengen Modells einer solchen Situation ist es oft nötig, von Formeln zu Funktionen überzugehen.
Diese Bemerkungen zum Funktionsbegriff stellen dar worauf es dabei ankommt. Sie werden dir bei den nachfolgenden Aufgaben helfen.
|
In dieser Aufgabe sollst du den bereits bekannten Zusammenhang zwischen der Gesprächsdauer und der Höhe der Telefonrechnung als Funktion formulieren. 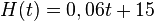 beschrieben werden.
zu definieren? Gib die Definitions- und Zielmenge an!
|
-
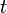 kann Werte
kann Werte 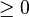 annehmen.
annehmen.
- Definitionsmenge ist
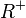 , Zielmenge ist
, Zielmenge ist 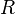 .
.
- Die unabhängige Variabel ist
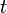 , die abhängige Variable
, die abhängige Variable 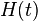 .
.
-
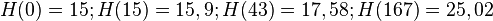
-
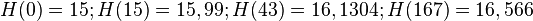
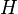 im strengen mathematischen Sinn als Funktion Fehler beim Parsen(Syntaxfehler): H: A \right B
im strengen mathematischen Sinn als Funktion Fehler beim Parsen(Syntaxfehler): H: A \right B

