Monotonie: Unterschied zwischen den Versionen
(→Monotonie) |
|||
| (10 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | zurück zu [[Funktionen_Einstieg/Eigenschaften von Funktionen|Eigenschaften von Funktionen]] | ||
| + | |||
| + | ---- | ||
| + | |||
{{Arbeiten|NUMMER=1| | {{Arbeiten|NUMMER=1| | ||
ARBEIT= | ARBEIT= | ||
Betrachte die folgenden Funktionen im angegebenen Intervall. Die Funktionen sind durch Funktionsterm und Graph gegeben. <br> | Betrachte die folgenden Funktionen im angegebenen Intervall. Die Funktionen sind durch Funktionsterm und Graph gegeben. <br> | ||
| − | a) <math>f:x \rightarrow x^2</math> | + | a) <math>f:x \rightarrow x^2</math> für <math>x \in R^+</math> <center>[[datei:Monotonie_quadratfunktion.jpg]]</center> |
| − | b) <math>f:x \rightarrow sin(x)</math> | + | b) <math>f:x \rightarrow sin(x)</math> im Intervall [0;1] <center>[[datei:Montonie_sinusfunktion.jpg]]</center> |
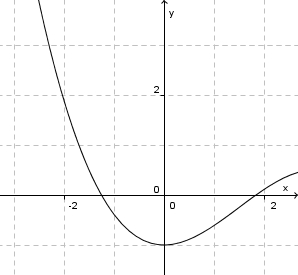
| − | c) <math>f:x \rightarrow -\frac{1}{9}x^3 + \frac{1}{2}x^2-1</math> | + | c) <math>f:x \rightarrow -\frac{1}{9}x^3 + \frac{1}{2}x^2-1</math> im Intervall [0;3] <center>[[datei:Monotonie_kubikfunktion.jpg]]</center> |
Was fällt dir auf? | Was fällt dir auf? | ||
| Zeile 18: | Zeile 22: | ||
Dieser Begriff des Ansteigens eines Funktionsgraphen fassen wir genauer und benennen ihn. | Dieser Begriff des Ansteigens eines Funktionsgraphen fassen wir genauer und benennen ihn. | ||
| − | {{ | + | {{Merksatz|MERK= |
Eine Funktion <math> f</math> heißt '''streng monoton zunehmend''' im Intervall [a;b], wenn für alle <math> x_1,x_2 \in [a;b]</math> gilt: <math>x_1 < x_2 \Rightarrow f(x_1) < f(x_2)</math> | Eine Funktion <math> f</math> heißt '''streng monoton zunehmend''' im Intervall [a;b], wenn für alle <math> x_1,x_2 \in [a;b]</math> gilt: <math>x_1 < x_2 \Rightarrow f(x_1) < f(x_2)</math> | ||
}} | }} | ||
| Zeile 29: | Zeile 33: | ||
Betrachte die folgenden Funktionen in den angegebenen Intervallen Quadratfunktion in den angegebenen Intervallen | Betrachte die folgenden Funktionen in den angegebenen Intervallen Quadratfunktion in den angegebenen Intervallen | ||
</center> | </center> | ||
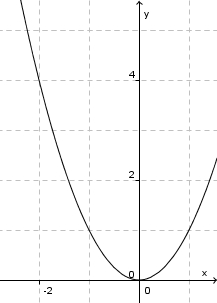
| − | a) <math>f:x \rightarrow x^2</math> | + | a) <math>f:x \rightarrow x^2</math> für <math>x \in R^-</math> <center>[[datei:Monotonie_quadratfunktion2.jpg]]</center><br> |
| − | b) <math>f:x \rightarrow sin(x)</math> | + | b) <math>f:x \rightarrow sin(x)</math> im Intervall [2;3] <center>[[datei:Montonie_sinusfunktion.jpg]]</center> |
| − | c) <math>f:x \rightarrow -\frac{1}{9}x^3 + \frac{1}{2}x^2-1</math> | + | c) <math>f:x \rightarrow -\frac{1}{9}x^3 + \frac{1}{2}x^2-1</math> im Intervall [-3;0] <center>[[datei:Monotonie_kubikfunktion2.jpg]]</center> |
Was stellst du nun fest? Was haben alle drei Graphen in den angegebenen Intervallen gemeinsam? | Was stellst du nun fest? Was haben alle drei Graphen in den angegebenen Intervallen gemeinsam? | ||
| Zeile 45: | Zeile 49: | ||
Auch diesen Begriff des Fallens eines Funktionsgraphen fassen wir - analog zu oben - genauer und benennen ihn. | Auch diesen Begriff des Fallens eines Funktionsgraphen fassen wir - analog zu oben - genauer und benennen ihn. | ||
| − | {{ | + | {{Merksatz|MERK= |
Eine Funktion <math> f</math> heißt '''streng monoton abnehmend''' im Intervall [a;b], wenn für alle <math> x_1,x_2 \in [a;b]</math> gilt: <math>x_1 < x_2 \Rightarrow f(x_1) > f(x_2)</math> | Eine Funktion <math> f</math> heißt '''streng monoton abnehmend''' im Intervall [a;b], wenn für alle <math> x_1,x_2 \in [a;b]</math> gilt: <math>x_1 < x_2 \Rightarrow f(x_1) > f(x_2)</math> | ||
}} | }} | ||
| − | + | In diesem Video wird nochmals der Begriff '''Monotonie''' erklärt: | |
| + | |||
| + | <center>{{#ev:youtube |rsLOKo6iwqs|350}}</center> | ||
| − | |||
Man könnte diese Begriffe '''monoton zunehmend''' und '''monoton abnehmend''' auch für die Funktionsgraphen übernehmen, hier verwendet man allerdings '''monoton steigend''' und '''monoton fallend'''. | Man könnte diese Begriffe '''monoton zunehmend''' und '''monoton abnehmend''' auch für die Funktionsgraphen übernehmen, hier verwendet man allerdings '''monoton steigend''' und '''monoton fallend'''. | ||
| − | {{ | + | {{Merksatz|MERK= |
Eine Funktionsgraph <math> G_f</math> heißt '''streng monoton steigend''' im Intervall [a;b], wenn die Funktion <math>f</math> dort streng monoton zunehmend ist, <br> | Eine Funktionsgraph <math> G_f</math> heißt '''streng monoton steigend''' im Intervall [a;b], wenn die Funktion <math>f</math> dort streng monoton zunehmend ist, <br> | ||
d.h.für alle <math> x_1,x_2 \in [a;b]</math> gilt: <math>x_1 < x_2 \Rightarrow f(x_1) < f(x_2)</math> | d.h.für alle <math> x_1,x_2 \in [a;b]</math> gilt: <math>x_1 < x_2 \Rightarrow f(x_1) < f(x_2)</math> | ||
| Zeile 62: | Zeile 67: | ||
d.h. für alle <math> x_1,x_2 \in [a;b]</math> gilt: <math>x_1 < x_2 \Rightarrow f(x_1) > f(x_2)</math> | d.h. für alle <math> x_1,x_2 \in [a;b]</math> gilt: <math>x_1 < x_2 \Rightarrow f(x_1) > f(x_2)</math> | ||
}} | }} | ||
| + | |||
| + | |||
{{Arbeiten|NUMMER=3|ARBEIT= | {{Arbeiten|NUMMER=3|ARBEIT= | ||
| Zeile 93: | Zeile 100: | ||
</div> | </div> | ||
| − | + | {{Arbeiten|NUMMER=4|ARBEIT= | |
| + | |||
| + | Teste dich! Klicke im folgenden Quiz auf die richtigen Zuordnungen! | ||
| + | |||
| + | Du kannst als Hilfe GeoGebra öffnen, dir die Graphen der Funktionen zeichnen lassen und dann die Fragen beantworten. | ||
| + | }} | ||
| + | |||
| + | |||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| Zeile 121: | Zeile 135: | ||
</div> | </div> | ||
| + | |||
| + | {{Arbeiten| | ||
| + | NUMMER=5| | ||
| + | ARBEIT= Bestimme die Parameterwerte r, für die die Funktion <math> f: x \rightarrow rx^2 - 2</math> so, dass <math> f</math><br> | ||
| + | # im Intervall [1;3] monoton zunehmend ist. | ||
| + | # im Intervall [1;3] monoton abnehmend ist. | ||
| + | # im Intervall [-2,5;-1] monoton zunehmend ist. | ||
| + | # im Intervall [-2,5;-1] monoton abnehmend ist. | ||
| + | # im Intervall [-1;1] monoton zunehmend ist. | ||
| + | <center> | ||
| + | <ggb_applet width="566" height="370" version="4.0" ggbBase64="UEsDBBQACAAIAPQ9I0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAPQ9I0AAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vjrb9s2EP/c/hUHfWqH2ib1slzYLdYCxQKk3YB0w7APAyiJttlIoiZSfhT943ckJVlOH0iToR1qxOHreM/fHS9ZPj+UBex4o4SsVh6dEg94lclcVJuV1+r1JPGeP3u43HC54WnDYC2bkumVFxpKka88FiRzQpP5JAx4PAkJ4ZNkHpJJHCZxukizRURiD+CgxNNKvmElVzXL+FW25SW7lBnTVvBW6/rpbLbf76e9qKlsNrPNJp0eVO4BqlmplddNniK7s0v7wJL7hNDZn68vHfuJqJRmVcY9MCa04tnDB8u9qHK5h73I9XblRfPQgy0Xm62xaZF4MDNENTqk5pkWO67w6mhpbdZl7VkyVpnzB24GxWCOB7nYiZw3K49MgzAJA59EKGtB/WSBEmUjeKU7YtoJnfXsljvB946vmVmReElLWaTMsIQPH8AnPoEnZqBu8HGIY3dE3B4J3OC7IXRD5GhCdz10pKGjCR1NGHiwE0qkBV95a1YodKGo1g2Gb1grfSy41afbOJlPn6BNSrxH4oAgTpzPcZ+QJ+Yb4zc0B7NzI+lIqm7arxTai4zi+PYi/XsZGvQy/U+Z6UefMTP+glBn923spNFIJoqyP/b7kcTgS2belOjW9xMYh9/ExOWsT5Vllx2gtoa2Q4/mpTL5EiwgWhjYU4gwN+I5ojwCusBh7gNmA9AIwgiXNIHYjHMI5ngQQgAJGDoagE2OKMFf4dwyiyFCZmZ3jjkJFAWFEAVAbU6FgJkENi8xR/0AKaIIIrxkxFPfsAhiCGNcBQmEqKNJyTlFwgAv4hrF+xBQCMxlOgc/htjwo6FJ9TgxqiNLH2ICMTUMMasxo102I30CgbEm7twlqrrVZy7KyryfalkPsUBqrEensufq01lVfLAsWMoLfCiuTCQBdqwwGWEFrWWloQ+i7/Y2Dau3IlNXXGu8peAd27FLpvnhFVKrXralzWSlfmukfimLtqwUQCYLMugsCzqa+4PWuAhGB+H4IBodxKP5/JNyJZ5AqzjKl43qyVmeXxiKU2lAT/5aFccXDWfXtRTnZixn9s1Z8jYrRC5Y9QeC1UgxfoHhCTLlqn+CgtDvFZFNfnVUiGA4/MUbiTUmDqeL8Qdz7OiOaEimZPwxhSljJvnCxfmlBKUdP3fmZPPdECJ24IP1m8Zkdme5WVyoF7I4bVn7X7Jat43tHlCHxlj1c7UpuMWILbf4NGfXqTxcOXAEjtfbY40r4hRIN9bvgLXBjyIk6MbUjZbGaDZQEUtDLAXp0Sby4ZwufEthx9SNlgrh61TrLKW9mZT0YoSyFY14Z3ljsW8e+rYS+rJfaJFdd5ZSR/+mLVM+IOicJf2PWC5nNxC2vOZNxYsO0BjJVrbK5ecI6znPRIlLd9A5hJlg/Y4KuN2cbxre613Yvsy5y56SMVY/2rasXjWyvKh2bxEJNxRYznotlyprRG0AByk+Atf8hKlcKIZvSD6+ZzIQTc/MW4Hu0cY1mJut3srGtl5YUnA0iVfwEvss0BZcVVvyRmSDoxvbw6FSbae36X6t5sbLINN3WOtuBOcURTz+DPyAFfWWmc6PdiBjR96cucZyey3zXnAntjAtI5QCn8AJwr1kBywPyC9VWAY1Ns0Yi+rUNDvNujKCDYdpyQ+m5TKTo3kwzWQtDiOHoo/Ee8QEOzPmlAYaK/Q1tqHK5qrustJOfhF5zqtBW1YhemwMsEjVzlzA94E7ZA9XazTf1oNR5LvAmBAd6galGTadi9f4F8jBvESPDo9hBQ38BIe/H/mPYQK+e5jOw7puKwsF78TgyzEcpcBtgkhuGURyV1eeuePMNMNrUJvdx6yIuroXBXe37O4B70qEMuikHTgtNt8j0IesuwsI+T+Vu6JciRRlXYhM6K/wa/qD+jX4zn7N7uNXStxDbfz7//KrP42+q1vzH9Ot36QKzMatg+3Pu/81PfsXUEsHCMyFi3W1BQAACBMAAFBLAQIUABQACAAIAPQ9I0DWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgA9D0jQMyFi3W1BQAACBMAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAABMBgAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | </center> | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | # r > 0 | ||
| + | # r < 0 | ||
| + | # r < 0 | ||
| + | # r > 0 | ||
| + | # es gibt kein r }} | ||
| + | |||
| + | {{Arbeiten| | ||
| + | NUMMER=5| | ||
| + | ARBEIT= Bestimme die Parameterwerte r, für die die Funktion <math> f: x \rightarrow sin(rx) + 1</math> so, dass <math> f</math><br> | ||
| + | # im Intervall [<math> \frac{\pi}{2};\pi</math>] monoton zunehmend ist. | ||
| + | # im Intervall [<math> \frac{\pi}{2};\pi</math>] monoton abnehmend ist. | ||
| + | <center> | ||
| + | <ggb_applet width="566" height="260" version="4.0" ggbBase64="UEsDBBQACAAIAFM/I0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAFM/I0AAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vdbb9s2FH5Of8WBnrqttklR18JusW4oViDtBqQbhr1REmOz0W0i5UvRH79DUrLlpCmaZejDjDi8HZ77d3i8fLmvStiKTsmmXnl0TjwQdd4Usl6vvF5fzxLv5Ysny7Vo1iLrOFw3XcX1ygsMpSxWHmdJTGgSzwImollAiJglcUBmUZBEWZrlaUgiD2Cv5PO6eccroVqei6t8Iyp+2eRcW8Ebrdvni8Vut5uPouZNt16s19l8rwoPUM1arbxh8hzZnV3aMUvuE0IXf769dOxnslaa17nwwJjQyxdPLpY7WRfNDnay0JuVF8aBBxsh1xu0iSWJBwtD1KJDWpFruRUKr06W1mZdtZ4l47U5v3AzKI/meFDIrSxEt/LInAVJwHwSoqyU+kmKEptOiloPxHQQuhjZLbdS7BxfM7Mi8ZJumjLjhiV8+gQ+8Qk8MwN1g49DFLkj4vYIc4PvhsANoaMJ3PXAkQaOJnA0AfNgK5XMSrHyrnmp0IWyvu4wfMe10odSWH2GjZP59BnapORHJGYE88T5HPcJeWa+EX4Dc7A4N5JOpOquf6DQUWQYRV8v0n+UoWyU6X/OTD+8x8zoC0Kd3V9jJw0nMlGU/bPfOxLZl8y8LdGtHycwCr6JicvFCJXlgA5QG0M7ZI8WlTJ4YSmEqUl7CiFiI4oxy0OgKQ6xD4gGoCEEIS5pApEZY2AxHgTAIAFDRxlYcIQJ/gtiyyyCEJmZ3RgxCRQFBRAyoBZTASCSwOISMeozpAhDCPGSEU99w4JFEES4YgkEqKOBZEyRkOFFXKN4HxgFZi7TGPwIIsOPBgbqUWJUR5Y+RAQiahgiqhHRDs1InwAz1kSDu2Td9vrMRXlVjFPdtMdYIDXWo1PZc/XprCpeLEueiRIfiisTSYAtLw0irKDrptYwBtF3e+uOtxuZqyuhNd5S8IFv+SXXYv8aqdUo29LmTa1+6xr9U1P2Va0A8qYkR52bkk7m/lFrXLDJQTA9CCcH0WQef1ZugyfQK4Hym06N5Lwo3hiKU2lAT/5al4dXneA3bSPPzVgu7JuzFH1eykLy+g9MViPF+AWOT5ApV+MT5DN/VKTpiquDwgyG/V+ia/AsCubp9IMYO7gjGpA5mX5MYcq5AV+Qnl9KUNrh/jMrXGyPMeJ7cTR/3RloD6abxRv1qilPW9YBP/FW951tH1CJzpj1Y70uhU0SW2/xbc5vsmZ/5bKDOV7vDy2uiFMgW1vHAxYHPwyRYBgzN1oao9mRilgaYinImG6yOJ7T1LcUdszcaKkwf51qg6V0NJOSUYxUtqQR7ww4NvnNS9/XUl+OCy3zm8FS6ujf9VUmTilkCH6Wri0x/VYYkziNmB/FaZCkUXRLKP0vhNpUvJWEyxvR1aIcch5j3Te9chCewKEQuaxw6Q4Gl3ETzt9RAbdbiHUnBnpe2tbNOdSekmk639m2rF53TfWm3r7HXLmlwHIxarlUeSdbk5KQ4TtxI05ZV0jF8ZkppvcMSNH03Dwn6B5tXIPw7fWm6Wx3hlUHR4PNUlTYioG26Vf3lehkfnR0Z9s8VKof9KbzocAZL0OTfcByeCs4o8svlnh8T4ICL9sNN80hHdKQH0R35hrL7W1TjIIHsaXpKqGS+ErOEBAV32MFQX6Zwkqpsa/GWNSnvtppNlQabFJM1743XZmZHAyazORa7icORR/Jj5gT/MyYE1A0FvEb7FSVRbMecGsnv8iiEPVRW15j9tgYYB1rnbmAT4hwmX282qL5tmJMIj8E5k6IjB5HX3Pvy7GYpPLdYITUlYKQTeJBvjIe5LEWDphQJhx0iIaNykeM7H114d8EQfxduyvKlQhZtaXMpX6Am7P/qZvZnAY0TP0oZGGSxin7Bl7etx3yM6aMzsNf3HvTeT3dfwcr7Jnqpx18D7j4AdxPw1uhue5rW9hO7n9MeO6WpAfG5uHemvpjMS3VtmUafv6/+AdQSwcIvPHKrL0FAACbEAAAUEsBAhQAFAAIAAgAUz8jQNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACABTPyNAvPHKrL0FAACbEAAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAFQGAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | </center> | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | # <math>0 \le r \le 0,5</math> oder <math>-1,5 \le x \le -1</math> | ||
| + | # <math>1 \le x \le 1,5</math> oder <math>-0,5 \le x \le 0</math> | ||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
zurück zu [[Funktionen_Einstieg/Eigenschaften von Funktionen|Eigenschaften von Funktionen]] | zurück zu [[Funktionen_Einstieg/Eigenschaften von Funktionen|Eigenschaften von Funktionen]] | ||
Aktuelle Version vom 31. Mai 2012, 14:53 Uhr
zurück zu Eigenschaften von Funktionen
Dieser Begriff des Ansteigens eines Funktionsgraphen fassen wir genauer und benennen ihn.
|
Merke:
Eine Funktion |
Auch diesen Begriff des Fallens eines Funktionsgraphen fassen wir - analog zu oben - genauer und benennen ihn.
|
Merke:
Eine Funktion |
In diesem Video wird nochmals der Begriff Monotonie erklärt:
Man könnte diese Begriffe monoton zunehmend und monoton abnehmend auch für die Funktionsgraphen übernehmen, hier verwendet man allerdings monoton steigend und monoton fallend.
|
Merke:
Eine Funktionsgraph Eine Funktionsgraph |
|
Teste dich! Klicke im folgenden Quiz auf die richtigen Zuordnungen! |
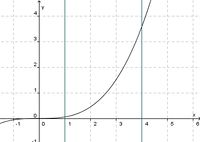 (streng monoton steigend) (!streng monoton fallend) (!weder noch)
(streng monoton steigend) (!streng monoton fallend) (!weder noch)
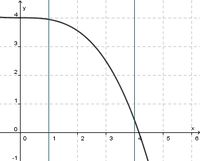 (!streng monoton steigend) (streng monoton fallend) (!weder noch)
(!streng monoton steigend) (streng monoton fallend) (!weder noch)
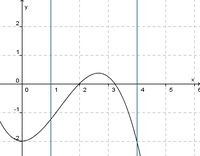 (!streng monoton steigend) (!streng monoton fallend) (weder noch)
(!streng monoton steigend) (!streng monoton fallend) (weder noch)
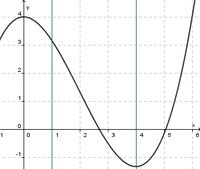 (!streng monoton steigend) (streng monoton fallend) (!weder noch)
(!streng monoton steigend) (streng monoton fallend) (!weder noch)
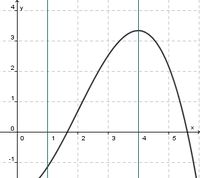 (streng monoton steigend) (!streng monoton fallend) (!weder noch)
(streng monoton steigend) (!streng monoton fallend) (!weder noch)
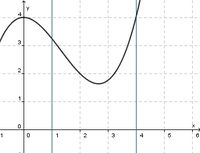 (!streng monoton steigend) (!streng monoton fallend) (weder noch)
(!streng monoton steigend) (!streng monoton fallend) (weder noch)
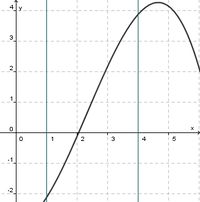 (streng monoton steigend) (!streng monoton fallend) (!weder noch)
(streng monoton steigend) (!streng monoton fallend) (!weder noch)
|
Teste dich! Klicke im folgenden Quiz auf die richtigen Zuordnungen! Du kannst als Hilfe GeoGebra öffnen, dir die Graphen der Funktionen zeichnen lassen und dann die Fragen beantworten. |
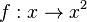 im Intervall [2;8]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
im Intervall [2;8]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
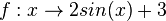 im Intervall [
im Intervall [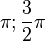 ]
(!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch)
]
(!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch)
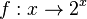 im Intervall [-1;4]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
im Intervall [-1;4]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
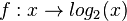 im Intervall [-1;4]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
im Intervall [-1;4]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
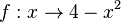 im Intervall [-1;4]
(!streng monoton zunehmend) (!streng monoton abnehmend) (weder noch)
im Intervall [-1;4]
(!streng monoton zunehmend) (!streng monoton abnehmend) (weder noch)
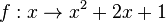 im Intervall [2;8]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
im Intervall [2;8]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
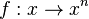 mit
mit 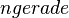 im Intervall [-4;-1]
(!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch)
im Intervall [-4;-1]
(!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch)
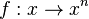 mit
mit 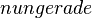 im Intervall [-3;9]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
im Intervall [-3;9]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
|
Bestimme die Parameterwerte r, für die die Funktion
|
- r > 0
- r < 0
- r < 0
- r > 0
- es gibt kein r
|
Bestimme die Parameterwerte r, für die die Funktion
|
-
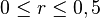 oder
oder 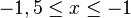
-
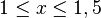 oder
oder 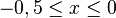
zurück zu Eigenschaften von Funktionen
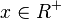
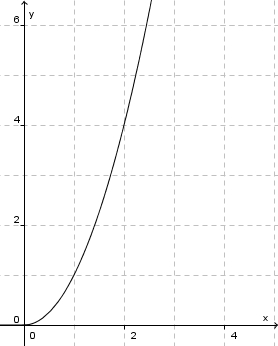
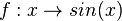 im Intervall [0;1]
im Intervall [0;1] 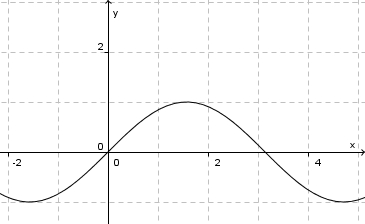
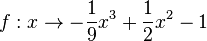 im Intervall [0;3]
im Intervall [0;3] 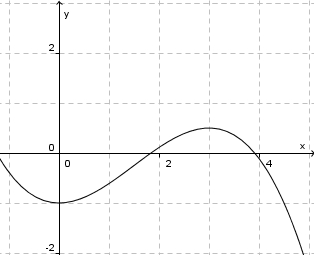

 heißt streng monoton zunehmend im Intervall [a;b], wenn für alle
heißt streng monoton zunehmend im Intervall [a;b], wenn für alle ![x_1,x_2 \in [a;b]](/images/math/4/8/9/489a4ad3c2410297428c10a130e7cc95.png) gilt:
gilt: 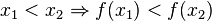
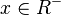
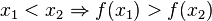
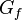 heißt streng monoton steigend im Intervall [a;b], wenn die Funktion
heißt streng monoton steigend im Intervall [a;b], wenn die Funktion 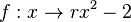 so, dass
so, dass 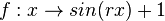 so, dass
so, dass 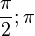 ] monoton zunehmend ist.
] monoton zunehmend ist.

