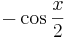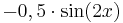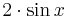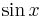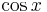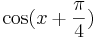Testseite: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
K |
|||
| Zeile 1: | Zeile 1: | ||
| + | {{Arbeiten| | ||
| + | NUMMER=22| ARBEIT= | ||
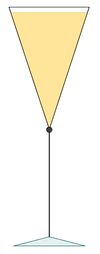
| + | [[Datei:Sektglas.jpg|right|100px]] | ||
| + | <big>Wann ist ein Sektglas halb voll?</big> | ||
| + | |||
| + | Ein Sektglas ist oben kegelförmig. Der Durchmesser der Deckfläche ist 5cm, die Höhe H des Kegels 8cm. Bei der Füllhöhe h = 7,639cm ist das Glas mit 0,2l gefüllt. (1 l = 1 dm³) | ||
| + | |||
| + | Nun interessiert die Frage, wann ist das Glas halb voll?<br> | ||
| + | Dabei verstehen wir unter halb voll, dass das Glas das halbe Volumen, also 0,1l enthalten soll. | ||
| + | |||
| + | Mit h bezeichnen wir die Füllhöhe. | ||
| + | |||
| + | 1. Bestimme mit Hilfe des Strahlensatzes einen Zusammenhang zwischen h, H und r. | ||
| + | |||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
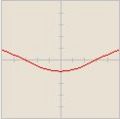
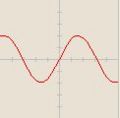
<!-- 1 '''Ordne den Funktionsgraphen den richtigen Term zu.''' | <!-- 1 '''Ordne den Funktionsgraphen den richtigen Term zu.''' | ||
Version vom 25. Juni 2012, 14:07 Uhr
|
Wann ist ein Sektglas halb voll? Ein Sektglas ist oben kegelförmig. Der Durchmesser der Deckfläche ist 5cm, die Höhe H des Kegels 8cm. Bei der Füllhöhe h = 7,639cm ist das Glas mit 0,2l gefüllt. (1 l = 1 dm³) Nun interessiert die Frage, wann ist das Glas halb voll? Mit h bezeichnen wir die Füllhöhe. 1. Bestimme mit Hilfe des Strahlensatzes einen Zusammenhang zwischen h, H und r. |
2
4
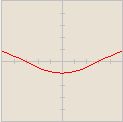
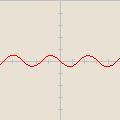
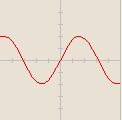
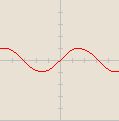
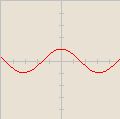
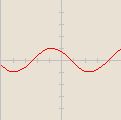
![-\cos [\frac{x}{2}]](/images/math/2/1/2/212d1079c931b2f1abf9a4fc6603a1a1.png)
![-0,5 \cdot \sin [2x]](/images/math/5/8/9/5893264368b318e2deb7f48a7cc94978.png)
![2 \cdot \sin [x]](/images/math/0/c/8/0c861e4179c5f92a8c48576d0f4477a3.png)
![\cos[x+\frac{\pi}{4}]](/images/math/b/4/e/b4e45ae4dc5d89cbe8a9b9a3366947ea.png)