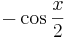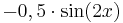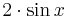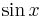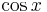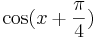Testseite: Unterschied zwischen den Versionen
| Zeile 22: | Zeile 22: | ||
Im folgenden Applet ist die Füllhöhe h als Funktion des Quotienten <math>\frac{V}{V_0}</math> angegeben. | Im folgenden Applet ist die Füllhöhe h als Funktion des Quotienten <math>\frac{V}{V_0}</math> angegeben. | ||
| − | + | <center> | |
| − | <ggb_applet width="449" height="520" version="4.0" ggbBase64="UEsDBBQACAAIAFyD2UAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACABcg9lAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1aW2/buBJ+7v4KQk/dg1oWL7oVdhfJpsEWaPeCdBcH5+EsaImx2ciSIsmJHeyP3yEpyZLVpHGStm6NuhTF0QznmyvlTH5aLxN0JYpSZunUwrZjIZFGWSzT+dRaVeejwPrp1Q+TucjmYlZwdJ4VS15NLaYoZTy1IodGTODZiAbCHTGP8xEP3GhEz0PhxngW8BAo0bqUL9PsV74UZc4jcRYtxJK/zSJeacGLqspfjsfX19d2I8rOivl4Pp/Z6zK2EGwzLadWffES2PUeuqaanDgOHv/33VvDfiTTsuJpJCykVFjJVz88m1zLNM6u0bWMqwWo4foWWgg5X4BOHoPJWBHlAEguokpeiRIe7Uy1ztUytzQZT9X6M3OFklYdC8XySsaimFqOTXw/CEPKqMtY4PqBhbJCirSqaXEtc9xwm1xJcW3YqistkVmoyrJkxhVH9M8/iDjEQS/UgM1AYPA8s+SYew41AzEDM4NraJh5nBlSZmiYoWHUQleylLNETK1znpSAoEzPC7BeOy+rTSL0fuobW+3xC9CplDdATB0wvoEc7jvOC/X14MvUwrivJO5IrYrVnkIbkYyF9xdJHqUobWRi4g9lEvcWNb07hBq976MndjvQgij9T38HEuldau5KNPPHCfTYF1FxMm5CZVJHByoXirb2nkosSxUvNERuqNweIxdiw/PBy12EQxh8giAaEHYRc2GKA+Sp0UfUhwWGKAqQosMU6eBwA/iP+ZqZh1xgpu76EJMIgyCGXIqwjimGIJKQjkuIUUKBwnWRCw8p8ZgoFtRDzIMZDRCDPaqQ9DEQUngQ5iCeIIoRVQ9jHxEPeYofZirUvUBtHVgS5DnIw4ohRDVEtIlmoA8QVdp4NVwyzVdVD6JoGbcGqLK8vQZySEjbtGcSVC8rPpskfCYSKBRnypQIXfFEhYSWdJ6lFWqDw9ybFzxfyKg8E1UFT5XoA7/ib3kl1qdAXTayNW2UpeXvRVb9nCWrZVoiFGWJ0246S3DnmrS7hgntLLDugttZ8DrX/kflZrCCVqUA+VlRNuQ8jt8oim1uACh/S5PNcSH4RZ7JvhqTsa45E7GKEhlLnv4F3qqkKFxQW4JUvmpKEAtJs5GsiM82JbgwWv9PFBngGAZ22P1AztmYJeZ6/SXYWsRV8LGwvwDVZ1MvuY7tdD/MSBZXrYH4WrS6zwtd+drrN+VxlmydRyv/M8+rVaFbB0iNhVLpKJ0nQjuITrZQl6OLWbY+M55BDa/3mxxmjpE/m2vQEWQG4rpAUI8zM2oatbGWytE0jqZwGleTcbuOAVNFoceZGTUV+K7ZWq0obrTETiNGljqfOVYvarTjT61LC61SWb01MwggGV3UqmLzwK+r5Uxs/UcRnEjTk5hmqy8Gf1TM4knETMY7bji5EEUqktrrweCrbFWaIO4ERCwiuYSpWaiB48qof8KezN1YzAtR0/NEN28GVr3qdB16cFuzOi2y5Zv06j14zM4GJuNml5MyKmSu/BLNoFRciK3vxbLkUGni7nMqTAGNSFUUAKRSaEEAr6pFVuj+DPIOjCo6E7GEbgxV2gmVT7TIc93lKYRRNvsAmW9brAxBBygguMUjEU/yBVedYK1zwjei6KGg2b3L4l1sAHqtAKSBXDFQ9s6FMK5S1VGDcmCog66XyADuEq2n1si3PQoJYQOXxIZAuulupQ2BClLzBTSgpY7Tlre6+EXGsdB12SSIy9Q8UhonlMs8kZGsai8zcN4N7Ow7A/aL4hplyyVPY5TqbupNWkHoA4TWtsJzR/ku4lghbUBcVc3CieFXcxnYSSfy1g4nnzKUzjgDO6n+b26GmRkeaqot3OpR7cT6AsCmgY3DuiDoXaui0utCzN2dnHNPFxWH5aIPcdAGMVwDNgqe0j3F+jHuKYx78oF7vt7HPV8fjnuOSAO3h20MPa9C3GSIx3joXmgOg/10HzRPDwfNT4DZaSZqb8yzhBdPiPSZmKv7Ozi/NjifDHCe341zWXNrgJwPke61fI/OLfh+MAc1ysT2cIAZ9annhBg+n7mcaewSlbpaj4ZUN+w+L4TI1eHgt/R9wdNSvXw0NI0n7mvAE2PA04EB5X4GlAdiwNF3ZcE+5ulqKQoZdY5b+uUoT1YNGnZd/W+3w8cz1m1mwPdMVzVdmahXvGgpU81myde6OtfneqIso0xEbb93ziZMWyyw3Z2D+blcd041cFCRN3Aw4z01HmLHYbvruPdsJ3rWWecFiFN8anRzC8HNqbVBUxSg/6DL/z/HaIzoj1avoxrf3WnlT9xp7WnFO/olz6Ys9BxGHD/wiQ82OpDuaW7SWD5IY0f71Pujw6n3I+zZHmHY91gAmIch1ZZwHdsPvYBSzyNhQNRp68ZUrc/fU+UGYznA+HgfjI8PB+OvB/HvWbKZZ+kOwEcG4GMYyMd6qr8k8IsusCGLDRn/W80p9Lp/40/ZwQhtgG7ZPTSE96727etLx5jRxR0zuvuY8fYiuduYxA9rTO7c6qOP7MzGLqRRhokT+Ay8zDQnIwIJNggJdQkNHAwJ1n26BPuFm5VdOyg/PSBLDCtZ/T4Q5g4hDixRsIx6IX9Tv2L5XiwxOwRLlCr3KFWPkiS7FvFA4U4p3M9W35ap9jhkD89o0X5ntOhzn9H2zIKuTahHIAH6BAeEkDrWGLaD0CFh6Ps+c30/YN+QPXfPBAhY1YeC8+eXPw7OBcOjwPkq1RvZmuVbffG6v8HuPl39UQP5/PIFUmC2p6q6wxxi2W89/zic1lO1O/pt3jC13XR+CH2SZvO0cah+Vtk5n6oM45iWEg8SzeLuRDNw2cVXzTSP87t7g7e+J3jFnuAVXzfenzpqP9RRu4bcd7nXe5APD4vXx+JAdoMV1/Wq+Z1ttD2sfMZfNcfdX+z1387Ufwf66l9QSwcIZZjiNoAIAACkKgAAUEsBAhQAFAAIAAgAXIPZQEXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACABcg9lAZZjiNoAIAACkKgAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAABgJAAAAAA==" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br> | + | <ggb_applet width="449" height="520" version="4.0" ggbBase64="UEsDBBQACAAIAFyD2UAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACABcg9lAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1aW2/buBJ+7v4KQk/dg1oWL7oVdhfJpsEWaPeCdBcH5+EsaImx2ciSIsmJHeyP3yEpyZLVpHGStm6NuhTF0QznmyvlTH5aLxN0JYpSZunUwrZjIZFGWSzT+dRaVeejwPrp1Q+TucjmYlZwdJ4VS15NLaYoZTy1IodGTODZiAbCHTGP8xEP3GhEz0PhxngW8BAo0bqUL9PsV74UZc4jcRYtxJK/zSJeacGLqspfjsfX19d2I8rOivl4Pp/Z6zK2EGwzLadWffES2PUeuqaanDgOHv/33VvDfiTTsuJpJCykVFjJVz88m1zLNM6u0bWMqwWo4foWWgg5X4BOHoPJWBHlAEguokpeiRIe7Uy1ztUytzQZT9X6M3OFklYdC8XySsaimFqOTXw/CEPKqMtY4PqBhbJCirSqaXEtc9xwm1xJcW3YqistkVmoyrJkxhVH9M8/iDjEQS/UgM1AYPA8s+SYew41AzEDM4NraJh5nBlSZmiYoWHUQleylLNETK1znpSAoEzPC7BeOy+rTSL0fuobW+3xC9CplDdATB0wvoEc7jvOC/X14MvUwrivJO5IrYrVnkIbkYyF9xdJHqUobWRi4g9lEvcWNb07hBq976MndjvQgij9T38HEuldau5KNPPHCfTYF1FxMm5CZVJHByoXirb2nkosSxUvNERuqNweIxdiw/PBy12EQxh8giAaEHYRc2GKA+Sp0UfUhwWGKAqQosMU6eBwA/iP+ZqZh1xgpu76EJMIgyCGXIqwjimGIJKQjkuIUUKBwnWRCw8p8ZgoFtRDzIMZDRCDPaqQ9DEQUngQ5iCeIIoRVQ9jHxEPeYofZirUvUBtHVgS5DnIw4ohRDVEtIlmoA8QVdp4NVwyzVdVD6JoGbcGqLK8vQZySEjbtGcSVC8rPpskfCYSKBRnypQIXfFEhYSWdJ6lFWqDw9ybFzxfyKg8E1UFT5XoA7/ib3kl1qdAXTayNW2UpeXvRVb9nCWrZVoiFGWJ0246S3DnmrS7hgntLLDugttZ8DrX/kflZrCCVqUA+VlRNuQ8jt8oim1uACh/S5PNcSH4RZ7JvhqTsa45E7GKEhlLnv4F3qqkKFxQW4JUvmpKEAtJs5GsiM82JbgwWv9PFBngGAZ22P1AztmYJeZ6/SXYWsRV8LGwvwDVZ1MvuY7tdD/MSBZXrYH4WrS6zwtd+drrN+VxlmydRyv/M8+rVaFbB0iNhVLpKJ0nQjuITrZQl6OLWbY+M55BDa/3mxxmjpE/m2vQEWQG4rpAUI8zM2oatbGWytE0jqZwGleTcbuOAVNFoceZGTUV+K7ZWq0obrTETiNGljqfOVYvarTjT61LC61SWb01MwggGV3UqmLzwK+r5Uxs/UcRnEjTk5hmqy8Gf1TM4knETMY7bji5EEUqktrrweCrbFWaIO4ERCwiuYSpWaiB48qof8KezN1YzAtR0/NEN28GVr3qdB16cFuzOi2y5Zv06j14zM4GJuNml5MyKmSu/BLNoFRciK3vxbLkUGni7nMqTAGNSFUUAKRSaEEAr6pFVuj+DPIOjCo6E7GEbgxV2gmVT7TIc93lKYRRNvsAmW9brAxBBygguMUjEU/yBVedYK1zwjei6KGg2b3L4l1sAHqtAKSBXDFQ9s6FMK5S1VGDcmCog66XyADuEq2n1si3PQoJYQOXxIZAuulupQ2BClLzBTSgpY7Tlre6+EXGsdB12SSIy9Q8UhonlMs8kZGsai8zcN4N7Ow7A/aL4hplyyVPY5TqbupNWkHoA4TWtsJzR/ku4lghbUBcVc3CieFXcxnYSSfy1g4nnzKUzjgDO6n+b26GmRkeaqot3OpR7cT6AsCmgY3DuiDoXaui0utCzN2dnHNPFxWH5aIPcdAGMVwDNgqe0j3F+jHuKYx78oF7vt7HPV8fjnuOSAO3h20MPa9C3GSIx3joXmgOg/10HzRPDwfNT4DZaSZqb8yzhBdPiPSZmKv7Ozi/NjifDHCe341zWXNrgJwPke61fI/OLfh+MAc1ysT2cIAZ9annhBg+n7mcaewSlbpaj4ZUN+w+L4TI1eHgt/R9wdNSvXw0NI0n7mvAE2PA04EB5X4GlAdiwNF3ZcE+5ulqKQoZdY5b+uUoT1YNGnZd/W+3w8cz1m1mwPdMVzVdmahXvGgpU81myde6OtfneqIso0xEbb93ziZMWyyw3Z2D+blcd041cFCRN3Aw4z01HmLHYbvruPdsJ3rWWecFiFN8anRzC8HNqbVBUxSg/6DL/z/HaIzoj1avoxrf3WnlT9xp7WnFO/olz6Ys9BxGHD/wiQ82OpDuaW7SWD5IY0f71Pujw6n3I+zZHmHY91gAmIch1ZZwHdsPvYBSzyNhQNRp68ZUrc/fU+UGYznA+HgfjI8PB+OvB/HvWbKZZ+kOwEcG4GMYyMd6qr8k8IsusCGLDRn/W80p9Lp/40/ZwQhtgG7ZPTSE96727etLx5jRxR0zuvuY8fYiuduYxA9rTO7c6qOP7MzGLqRRhokT+Ay8zDQnIwIJNggJdQkNHAwJ1n26BPuFm5VdOyg/PSBLDCtZ/T4Q5g4hDixRsIx6IX9Tv2L5XiwxOwRLlCr3KFWPkiS7FvFA4U4p3M9W35ap9jhkD89o0X5ntOhzn9H2zIKuTahHIAH6BAeEkDrWGLaD0CFh6Ps+c30/YN+QPXfPBAhY1YeC8+eXPw7OBcOjwPkq1RvZmuVbffG6v8HuPl39UQP5/PIFUmC2p6q6wxxi2W89/zic1lO1O/pt3jC13XR+CH2SZvO0cah+Vtk5n6oM45iWEg8SzeLuRDNw2cVXzTSP87t7g7e+J3jFnuAVXzfenzpqP9RRu4bcd7nXe5APD4vXx+JAdoMV1/Wq+Z1ttD2sfMZfNcfdX+z1387Ufwf66l9QSwcIZZjiNoAIAACkKgAAUEsBAhQAFAAIAAgAXIPZQEXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACABcg9lAZZjiNoAIAACkKgAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAABgJAAAAAA==" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /></center><br> |
6. Bestimme graphisch und rechnerisch bei welcher Höhe h das eingefüllte Volumen 25%, 40%, 75% des Glasvolumens ist. | 6. Bestimme graphisch und rechnerisch bei welcher Höhe h das eingefüllte Volumen 25%, 40%, 75% des Glasvolumens ist. | ||
Version vom 25. Juni 2012, 15:42 Uhr
|
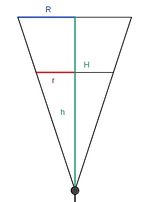
Wann ist ein Sektglas halb voll? Ein Sektglas ist oben kegelförmig. Der Radius R der Deckfläche ist 2,5 cm, die Höhe H des Kegels 8 cm. Bei der Füllhöhe h = 7,639 cm ist das Glas mit 0,2 l gefüllt. (1 l = 1 dm³) Nun interessiert die Frage, wann ist das Glas halb voll? Mit h bezeichnen wir die Füllhöhe. 1. Gib eine Formel für das Volumen mit Füllhöhe h an. 2. Bestimme mit Hilfe des Strahlensatzes einen Zusammenhang zwischen h, H , R und r. 3. Gib nun eine Abhängigkeit des Volumens von h an. 4. Löse dein Ergebnis aus 3. nach h auf. 5. Bestimme zu Im folgenden Applet ist die Füllhöhe h als Funktion des Quotienten
6. Bestimme graphisch und rechnerisch bei welcher Höhe h das eingefüllte Volumen 25%, 40%, 75% des Glasvolumens ist. |
1. 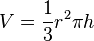
2. 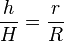
3. Mit 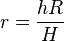 ergibt sich
ergibt sich 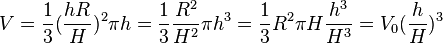 , wobei
, wobei 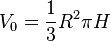 das Glasvolumen ist.
das Glasvolumen ist.
4. Fehler beim Parsen(Syntaxfehler): h = H \sqrt[3]{\frac{V}{V_0}
oder Fehler beim Parsen(Syntaxfehler): h = \sqrt[3]{\frac{3VH^2}{R^2 \pi}
5. ![h = H \sqrt[3]{\frac{1}{2}}=0,7937H\approx 0,8H = 6,4 cm](/images/math/9/2/d/92d01ff2d826057e1ebdc53561882b2a.png)
Ein kegelförmiges Sektglas ist also bei rund 80% der Füllhöhe halb voll.
6. 5,0 cm; 5,9 cm; 7,3 cm
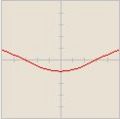
2
4
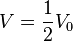 die passende Höhe h.
die passende Höhe h.
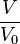 angegeben.
angegeben.
![-\cos [\frac{x}{2}]](/images/math/2/1/2/212d1079c931b2f1abf9a4fc6603a1a1.png)
![-0,5 \cdot \sin [2x]](/images/math/5/8/9/5893264368b318e2deb7f48a7cc94978.png)
![2 \cdot \sin [x]](/images/math/0/c/8/0c861e4179c5f92a8c48576d0f4477a3.png)
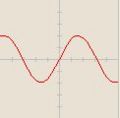
![\cos[x+\frac{\pi}{4}]](/images/math/b/4/e/b4e45ae4dc5d89cbe8a9b9a3366947ea.png)