Wurzelfunktion Übungen 1: Unterschied zwischen den Versionen
| (47 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | [[ | + | [[Wurzelfunktion_Startseite|Startseite]] --- [[Wurzelfunktion_Einführung|Die Wurzelfunktion]] - [[Wurzelfunktion_Übungen_1|Übungen]] - [[Wurzelfunktion_Anwendungen|Anwendungen]] - [[Wurzelfunktionen_Eigenschaften|Weitere Eigenschaften]] --- [[Wurzelfunktion_allgemeine_Wurzelfunktion|Die allgemeine Wurzelfunktion]] - [[Wurzelfunktion_Übungen_2|Übungen und Anwendungen]] --- [[Wurzelfunktion_Umkehrfunktion|Die Wurzelfunktion als Umkehrfunktion]] |
| − | + | __NOCACHE__ | |
---- | ---- | ||
| Zeile 6: | Zeile 6: | ||
{{Arbeiten| | {{Arbeiten| | ||
| − | NUMMER= | + | NUMMER=5| ARBEIT= |
Zeichne den Graphen der Funktionen <math>f:x \rightarrow x^2</math> im Intervall [0;3] und den Graphen der Funktion <math> g:x \rightarrow \sqrt x</math> im Intervall [0;7] in ein Koordinatensystem. | Zeichne den Graphen der Funktionen <math>f:x \rightarrow x^2</math> im Intervall [0;3] und den Graphen der Funktion <math> g:x \rightarrow \sqrt x</math> im Intervall [0;7] in ein Koordinatensystem. | ||
| Zeile 12: | Zeile 12: | ||
}} | }} | ||
| − | |||
| − | |||
| − | |||
| + | Neben der Quadratwurzelfunktion treten auch Funktionsterme der Art <br> | ||
| + | :::<math> a \sqrt x</math>,<br> | ||
| + | :::<math> a \sqrt x + b </math> und | ||
| + | :::<math> \sqrt {ax+b}</math> <br> | ||
| + | auf. Diese wirst du nun mit der Methode "Gruppenpuzzle" untersuchen. <br> | ||
| + | <br>Jede der folgenden Aufgabenstellungen (6, 7 und 8) wird von ein oder zwei Gruppen bearbeitet. Jedes Gruppenmitglied muss in der Lage sein, das Wissen weiterzugeben. <br>Überlegt gemeinsam, welche Informationen am wichtigsten sind und unbedingt in euren Mitschriften stehen sollten.<br> | ||
| + | |||
| + | {{Arbeiten| | ||
| + | NUMMER=6| ARBEIT= | ||
| + | Im Applet ist der Graph der Wurzelfunktion <math> f:x \rightarrow a \sqrt x </math> mit <math>x \in R^+_0</math> dargestellt.<br> | ||
| + | Variiere mit dem Schieberegler den Wert von <math>a</math>. | ||
| + | <center><ggb_applet width="697" height="467" version="4.0" ggbBase64="UEsDBBQACAAIAB2SnkAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAB2SnkAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVfbjts2EH1OvmKgp7aIbVJXO7ATNCmCBNgkBTYtir5REi0zK4mqSPkS5OM7JCVZ3k226aaosV7ehjwzZy6k18+PVQl73ioh641H58QDXmcyF3Wx8Tq9nS29588erwsuC562DLayrZjeeKGRFPnGi1YkTzLiz3gaBrOQh+ksDQIckiTcJmlAAx55AEclntbyHau4aljGr7Mdr9iVzJi2wDutm6eLxeFwmA9Qc9kWi6JI50eVe4Bq1mrj9Z2neNzFpkNgxX1C6OKPt1fu+JmolWZ1xj0wJnTi2eNH64Ooc3mAg8j1buMlBJXbcVHstDEFBwsj1CAhDc+02HOFWydDa7OuGs+KsdqsP3I9KEdzPMjFXuS83Xhk7i/JMqIkDpb+KlkmPoLIVvBa98K0B10Mx633gh/cuaZnIUMPtJRlysyR8Pkz+MQn8MQ01DU+NnHsloibI4FrfNeEromcTOi2h040dDKhkwkDD/ZCibTkG2/LSoUUinrbovvGsdKnklt9+omz+fQJ2qTEJxQOCMaJ4xznCXlivjF+Q7OwuDSSTlB12/1L0AEyXiXfDul/l6HBgElXy7uYfvQVM+N7QJ3d32InjSbUIpT9s987iMF9Zt5GdOPvA4zD/8XE9WJIlXWfHaB2RraPHs0rZfIlWEG0MmFPIcLciBOM8gjoCpvEB8wGoBGEEQ7pEmLTJhAkuBBCAEswcjQAmxzREv+FiT0shggPM7MJ5iRQBAohCoDanAoBMwlsXmKO+gFKRBFEuMnAU98cEcQQxjgKlhCijiYlE4qCAW7EMcL7EFAIzGaagB9DbM6joUn1eGlUxyN9iAnE1ByIWY0Z7bIZ5ZcQGGvini5RN52+oCir8qGrZTP6AqWxHp3LnqtPF1Xx0bpkKS/xorg2ngTYs9JkhAXaylrD4ETfzRUta3YiU9dca9yl4CPbsyum+fEVSqsB28pmsla/tlK/lGVX1QogkyUZdZYlnfT9UWscBJOFcLoQTRbiST/5Iq7EFegUR3zZqkGc5fkbI3EuDcjk+7o8vWg5u2mkuDRjvbB3zpp3WSlywerfMVgNiuEFhivIlqvhCgqD1aCIbPPrk8IIhuOfvJWmbPjm0j25kR+vzEhlzKRYuJqvpp8levzUr0VkTqYfGjoIvh89wY58NLJoRT7tv1EvZJmPJlsrX7JGd619I2AJbI3uP9dFyW0k2KKKF3B2k8rjtQuBwJ314dTgiDj8tLDsAlYAP8JLsejb1LVWxig2ShErQ6wEGWJK5OM6XflWwrapa60UBqlTrTeUDlZSMsAIZesW8S6yw0b4xjt60NVCX7kRZorIbnpTqdvwrqtSfg4UI/CLcI8P96q6hKFfhDn9JzDrxa14W9/wtuZlH97o8E52ymXrJPJznokKh26hJ44Zp/6GOrnZnBct7+VZaV9pjla7SqaRe2faHvWqldWbev8BI+aWAuvFoOVaZa1oTFxCilfCDT/HXi4Uwxsln+4z+YhsZObmQEK0YQsztdM72dqHGBYYbE0alrzCVxdoG4R1V/FWZCP5zL7oUKmu13v0miEeZPoRK98th9mBlcHlr4QpsLLZMfMOpH0wshNvL6ixp72V+QDcw5bmAQmVwAtxhmlRsSPmMp6XKiyKGp/Q6Iv6/IR2mvVFBZ8fpjoczQPMFg1XBjzYiuOEUORIfMKYYBfGnNNFY72+wUepsjmt++y1ndciz3k9astqjB7rAyxZjTMX8LbgLtrHrQ2ab+vGxPO9Y4yLjk2LaOYYSwqgHP4gOZqL6Yfjj7AB9VersWc3Xjp029U2CEbvbL2HeG8oRZT4dzxI7vXg++1WcW04X1nCZzS5z78PZ+whHrqP5Y1X9CQXjmQGP4Hh270D/oHm4kE0fy1JvpXiWeI4Xt6bQ9/H02JaW+x13v80ffY3UEsHCLK+mJGaBQAANw8AAFBLAQIUABQACAAIAB2SnkDWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAHZKeQLK+mJGaBQAANw8AAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAAxBgAAAAA=" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /></center> | ||
| + | Beschreibe, wie sich der Graph der Wurzelfunktion <math>x \rightarrow \sqrt x</math> ändert für | ||
| + | # <math>a = -1</math> | ||
| + | # <math>0 < a < 1</math> | ||
| + | # <math>1 < a</math> | ||
| + | # <math>a < 0</math> | ||
| + | |||
| + | Wie wirkt sich die Änderung des Parameters <math>a</math> auf die Definitions- und Wertemenge aus? | ||
| + | }} | ||
| − | |||
{{Arbeiten| | {{Arbeiten| | ||
| − | NUMMER= | + | NUMMER=7| ARBEIT= |
| − | Du betrachstest die Funktion <math>f: x \rightarrow \sqrt | + | Du betrachstest die Funktion <math>f: x \rightarrow a \sqrt x + b </math>. Im folgenden Applet kannst du mit den Schiebereglern die Werte für <math>a</math> und <math>b</math> verändern. <br>Anfangs ist <math>a = 1</math> und <math>b = 0</math>. Es ist der Graph der Quadratwurzelfunktion dargestellt. |
| − | + | ||
| − | + | <center><ggb_applet width="697" height="467" version="4.0" ggbBase64="UEsDBBQACAAIABCTnkAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIABCTnkAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vhbb9s2FH5uf8WBnnapbVJXu7BbrB2KBUjbAemGYW+URMtsJFETKV+K/vgdkpIiJ23WpcOAzYjD2yG/c/sOmayfH6sS9rxVQtYbj86JB7zOZC7qYuN1ejtbes+fPV4XXBY8bRlsZVsxvfFCIynyjRetSJ5kxJ/xNAxmIQ/TWRoEOCRJuE3SgAY88gCOSjyt5RtWcdWwjF9lO16xS5kxbYF3WjdPF4vD4TAfoOayLRZFkc6PKvcA1azVxus7T/G4s02HwIr7hNDFb68v3fEzUSvN6ox7YEzoxLPHj9YHUefyAAeR693GSwgqt+Oi2GljCg4WRqhBhzQ802LPFW6dDK3Numo8K8Zqs/7I9aAczfEgF3uR83bjkbm/JMuIkjhY+qtkmfgIIlvBa90L0x50MRy33gt+cOeanoUMPdBSlikzR8LHj+ATn8AT01DX+NjEsVsibo4ErvFdE7omcjKh2x460dDJhE4mDDzYCyXSkm+8LSsVulDU2xbDN46VPpXc6tNP3JhPn6BNSnxA4YBgnjif4zwhT8w3xm9oFhbnRtIJqm67vwk6QMar5Msh/a8yNBgw6Wp5F9OPPmNmfA+os/tL7KTRxLUIZX/s9w5icJ+ZtxHd+OsA4/BfMXG9GKiy7tkBamdk++zRvFKGL8EKopVJewoRciNOMMsjoCtsEh+QDUAjCCMc0iXEpk0gSHAhhACWYORoAJYc0RJ/hYk9LIYIDzOzCXISKAKFEAVALadCQCaB5SVy1A9QIoogwk0GnvrmiCCGMMZRsIQQdTSUTCgKBrgRxwjvQ0AhMJtpAn4MsTmPhobq8dKojkf6EBOIqTkQWY2MdmxG+SUExpq4d5eom06fuSir8qGrZTPGAqWxHt2UPVefzqrio3XJUl7iRXFlIgmwZ6VhhAXaylrDEETfzRUta3YiU1dca9yl4D3bs0um+fEVSqsB28pmslY/t1K/lGVX1QogkyUZdZYlnfT9UWscBJOFcLoQTRbiST/5JK7EFegUR3zZqkGc5fmFkbgpDejJt3V5etFydt1IcW7GemHvnDXvslLkgtW/YrIaFOMXGK4gW66GKygMVoMiss2vTgozGI6/81aasuGbS/fkRn68MiOVMUOxcDVfTT9LjPipX4vInEw/NHQQfD9Ggh35aGTRinzav1AvZJmPJlsrX7JGd619I2AJbI3uP9RFyW0m2KKKF3B2ncrjlUuBwJ317tTgiDj8tLDeBawAfoSXYtG3qWutjFFslCJWhlgJMuSUyMd1uvKthG1T11opTFKnWm8oHaykZIARytYt4p2xw2b4xjt60NVCX7oRMkVk172p1G1401Upv0kUI/CjcI8P96o6h6GfhDn9IzDrxa18W1/ztuZln94Y8E52yrF1kvk5z0SFQ7fQO46ZoP6COrnZnBct7+VZaV9pzq12lUwz9860PepVK6uLev8OM+aWAuvFoOVaZa1oTF5CilfCNb/JvVwohjdKPt1n+IjeyMzNgQ7RxlvI1E7vZGsfYlhgsDU0LHmFry7QNgnrruKtyEbnM/uiQ6W6Xu8xasbxINP3WPluBcwOrAwufyZNgZXNjpl3IO2TkZ14e+Yae9prmQ/APWxpHpBQCbwQZ0iLih2Ry3heqrAoanxCYyzqmye006wvKvj8MNXhaB5gtmi4MuDBVhwnDkUfiQ+YE+zMmBu6aKzX1/goVZbTumev7fwk8pzXo7asxuyxMcCS1ThzAW8L7rJ93Nqg+bZuTCLfB8aE6Ni0iGaOsU4BlMM/SI7mYvrm+C1sQP3RauzZjecB3Xa1TYIxOlvvIdEbShEl/p0Iknsj+Ha7VVwbn6+sw2c0uS++D/fYQyJ05uV7iZDeJgL5nxFh9R8kwsYreh4UjgcMvgNLie8hdc+1v2BD8SA2fC6EX8qEWeKosLw3wl+XzovpFWBfXf1/EJ79CVBLBwgj8/UrrQUAAN4QAABQSwECFAAUAAgACAAQk55A1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIABCTnkAj8/UrrQUAAN4QAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAARAYAAAAA" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /></center><br> | |
| − | < | + | 1. Variiere <math>a</math>. Was stellst du fest?<br> |
| + | Wie ändern sich die Definitionsmenge <math> D</math> und die Wertemenge <math>W</math>?<br> | ||
| + | 2. Stelle wieder <math> a = 1</math> ein. Was passiert, wenn du den Wert von <math>b</math> änderst? <br> | ||
| + | Wie ändern sich die Definitionsmenge <math> D</math> und die Wertemenge <math>W</math> der Funktion. | ||
| − | + | 3. Variiere nun a und b gleichzeitig und beobachte was passiert.<br> | |
| − | + | 4. Gib die Definitionsmenge <math> D</math> und die Wertemenge <math>W</math> der Funktion <math>f: x \rightarrow a \sqrt x + b </math> an. | |
| − | + | ||
}} | }} | ||
| − | |||
| − | |||
| − | + | {{Arbeiten| | |
| − | + | NUMMER=8| ARBEIT= | |
| − | + | Du betrachstest die Funktion <math>f: x \rightarrow \sqrt{ax + b} </math>. Im folgenden Applet kannst du mit den Schiebereglern die Werte für <math>a</math> und <math>b</math> verändern. <br>Anfangs ist <math>a = 1</math> und <math>b = 0</math>. Es ist der Graph der Quadratwurzelfunktion dargestellt. | |
| − | + | <center><ggb_applet width="792" height="408" version="4.0" ggbBase64="UEsDBBQACAAIAOyWnkAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACADslp5AAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1Y64/UNhD/DH/FKJ+gZW/jvBftggoV6kkHVDpaVf3mJN6suSROY2c3i/jjO7aTbPaAKy9VahF3tjPjefzm4YH1074qYc9ayUW9cciF6wCrM5Hzutg4ndouEufpk/vrgomCpS2FrWgrqjZOoDl5vnGi1HddLwkWfkS9ReARd7FKPLZYsWxLoijy4zxyAHrJH9fiFa2YbGjGrrMdq+iVyKgyindKNY+Xy8PhcDGquhBtsSyK9KKXuQNoZi03zrB5jOLOLh18w+65Lln+8fLKil/wWipaZ8wB7ULHn9y/tz7wOhcHOPBc7TZO4qIbO8aLHfoU+mjpUjM1CEjDMsX3TOLV2dH4rKrGMWy01vR7dgfl5I4DOd/znLUbx73wQgdEy1mtBioZtCzH++s9ZwcrSO+MjsABJUSZUi0D3r8Hz/VceKQXYhcPlyiyJNd+c327eHYJ7BJansBeDyxrYHkCyxP4Duy55GnJNs6WlhIx4/W2xXhNZ6mOJTP2DB9O/pJH6JPk75DZ14hakPG76z7SPxH+BJqwPHeSzLSqtvtCpaPKeOV9vkrvmxz1R53ex9z0wk+4Gd2h1Pr9OX6ScKYTVZm/5ucDjf5dbt7WaM/fpjAK/hUX18uxVNZDdYDcad4hexSrpK4XfwXhSqc9gRBrI4oxy0MgK1xiD7AagIQQhHgkCUR6jcGPkRCADwloPuKDKY4wwV9BbIRFEKIw/TXGmgSCigIIfSCmpgLASgJTl1ijno8cYQghXtLqiadF+BEEEZ78BAK0UZdkTJDRx4t4RvUe+AR8fZnE4EUQaXkk0KUeJdp0FOlB5EJEtECsaqxoW83In4CvvRkbGa+bTp1BlFX5uFWimWKB3NiPTn3O9qezNnhvXdKUlfgyXOtIAuxpqSvCKNqKWsEYRM9+K1ra7Hgmr5lSeEvCW7qnV1Sx/gVyy1G34c1ELX9thXouyq6qJUAmSneyWZRktvcmq/HgzwjBnBDOCNFsH39Ur0AKdJKhftHKkZ3m+aXmOLUGRPJ1XR6ftYzeNIKfu7Femkdmzbqs5Dmn9e+YrFqLxgXGN8e0q/HN8RN3NES0+fVRYgZD/ydrBfYYElys5n9iB46W5N8ioUSZUV17wer8ToKpcPwEzWpm+ylAtGeT70XL8/n+Uj4TZT4hYZx/ThvVtWZWwM7Yapd+qouSmQQxvRYf4uwmFf21zQzfynpzbPA0eJ4WBnTAxuCF+FYWw5ra1fBowyYu1/C4hsMdU43nE51oOIphTe1quDB3rWmDo2T0krijGi5NO3Ods6Ixib9xege6mqsre8IC4tnN4CqxF151VcpO+aMZfuZ2CLHT1bka8lE1x++iZr28lYbrG9bWrByyHgPeiU7aIp4VRM4yXuHREgbgqA7qb2iT/ZqzomUDPy3NtGZhNdSzhP7gsxH1ohXVZb1/gxlzy4D1crRyLbOWNzovIcWX4oadci/nkuJDk8/v6TJFNDL9oCAgSqOFBdypnWjNQIZ9B1ddnSWrcBgDZZKw7irW8mwCn5rJDo3qBrunqGngQaRvsSHeCpg5GB4kfyJNgZbNjup5kAzJSI+sPYPGSHsp8lHxoLbUgyRUHN/JBZZFRXt8GlFeKrFXKhylMRb1aZS2lg29BqcSPaj3ei7Tm6N+VfVmy/sZoIgRf4c5Qc+cOZWLwjZ+g7OqNDWthuo1m194nrN6spbWmD0mBtjJGusu4CPCbLZPVxt03/SNWeSHwPxjiNLbIXL/ZyFa/RdC1DctatNiBogL/Kdjj/KKB/1D2ID8q1UPKPwAPfwI6UM7YpwHdtvVpl6dk4jvGUX3zii+3m4lUxr3wIC+SO6M8ZcjfRdagM4PcG1ncPUPnc9AaftVKI1vK3G9r0YqtkiR+C6kvj6/vhXl5fwRMOPY8H8JT/4GUEsHCAEiWUqWBQAA6BAAAFBLAQIUABQACAAIAOyWnkBFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgA7JaeQAEiWUqWBQAA6BAAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAAuBgAAAAA=" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /></center><br> | |
| + | 1. Was passiert, wenn du den Wert von <math>b</math> änderst? Unterscheide <math> b > 0 </math> und <math> b < 0</math>. Gib die Nullstellen an! <br> | ||
| + | Wie ändern sich die Definitionsmenge und die Wertemenge der Funktion.<br> | ||
| + | 2. Stelle wieder <math> b = 0</math> ein. Variiere nun <math>a</math>. Was stellst du fest? <br> | ||
| + | Wie ändern sich die Definitionsmenge und die Wertemenge der Funktion.<br> | ||
| + | 3. Variiere nun a und b gleichzeitig und beachte was passiert.<br> | ||
| + | 4. Wo ist die Nullstelle der Funktion <math>f: x \rightarrow \sqrt{ax + b} </math>?<br> | ||
| + | 5. Gib die Definitionsmenge der Funktion <math>f: x \rightarrow \sqrt{ax + b} </math> an. | ||
}} | }} | ||
| + | '''Mischgruppen''' | ||
| + | <br>Jede Mischgruppe besteht aus mindestens einer Expertin bzw. einem Experten zu den obigen drei Aufgaben. Die Expertinnen und Experten fassen das Wesentliche für die anderen zusammen. Gemeinsam werden anschließend die folgenden drei Aufgaben gelöst.<br> | ||
{{Arbeiten| | {{Arbeiten| | ||
| − | NUMMER= | + | NUMMER=9| ARBEIT= |
| − | Skizziere und vergleiche die Graphen<br> | + | Skizziere und vergleiche die Graphen folgender Funktionen! Gib jeweils den Definitions- und Wertebereich an!<br> |
a) <math>f(x) = \sqrt{x+2}</math><br> | a) <math>f(x) = \sqrt{x+2}</math><br> | ||
b) <math>g(x) = \sqrt x + 2</math><br> | b) <math>g(x) = \sqrt x + 2</math><br> | ||
c) <math>h(x) = \sqrt{x-2}</math><br> | c) <math>h(x) = \sqrt{x-2}</math><br> | ||
| − | d) <math>k(x) = \sqrt x - 2</math><br> | + | d) <math>k(x)= 2\sqrt{x}</math> <br> |
| + | e) <math>l(x) = \sqrt x - 2</math><br> | ||
| + | f) <math>m(x) = -\frac{1}{2}\sqrt{x}</math><br> | ||
}} | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Arbeiten| | {{Arbeiten| | ||
| − | NUMMER= | + | NUMMER=10| ARBEIT= |
Es ist die Funktion <math>f: x \rightarrow \sqrt{25-x^2}</math> gegeben. | Es ist die Funktion <math>f: x \rightarrow \sqrt{25-x^2}</math> gegeben. | ||
# Bestimme die Definitionsmenge. | # Bestimme die Definitionsmenge. | ||
# Zeichne den Graphen. | # Zeichne den Graphen. | ||
| − | |||
# Wie kann man den Graphen noch bezeichnen? | # Wie kann man den Graphen noch bezeichnen? | ||
| − | + | # '''Bonus:''' Zeige, dass alle Punkte auf dem Graphen vom Ursprung den gleichen Abstand haben. | |
| − | + | ||
| − | # | + | |
| − | + | ||
| − | + | ||
| − | + | ||
}} | }} | ||
{{Arbeiten| | {{Arbeiten| | ||
| − | NUMMER= | + | NUMMER=11| ARBEIT= |
| − | a) | + | a) Löse dieses [http://www.johnny.ch/math/funktionen/wurz_funkt_quiz0.php Quiz].<br> |
| + | b) Öffne diese [http://www.fi.uu.nl/toepassingen/02023/toepassing_wisweb.xml?language=de Webseite]. | ||
| + | <br>Wähle Niveau 2 und finde zum gegebenen Funktionsgraph den passenden Funktionsterm.<br> | ||
Hinweis zur Schreibweise: Schreibe für <math>\sqrt x</math> sqrt(x). | Hinweis zur Schreibweise: Schreibe für <math>\sqrt x</math> sqrt(x). | ||
| + | }} | ||
| + | <br> | ||
| − | + | ||
| + | '''Präsentation der Ergebnisse - Staffellauf''' | ||
| + | <br>Präsentiert nun eure Ergebnisse zu den Aufgaben 9 und 10 aus der Mischgruppe in Form eines Staffellaufes. | ||
| + | <br>D.h.: Jede Teilaufgabe wird von einem/einer Schüler/in im Plenum vorgestellt. | ||
| + | |||
| + | |||
| + | |||
| + | Aufgabe 5: {{Lösung versteckt|1= | ||
| + | [[Datei:Wf_qf.jpg]] | ||
| + | |||
| + | Die Graphen von f und g sind symmetrisch zur Gerade y = x (1. Mediane). }} | ||
| + | |||
| + | Aufgabe 6: {{Lösung versteckt|1= | ||
| + | # Für <math>a = -1</math> wird der Graph der Wurzelfunktion <math>x \rightarrow \sqrt x</math> an der x-Achse gespiegelt. | ||
| + | # Für <math>0 < a < 1</math> wird der Graph der Wurzelfunktion <math>x \rightarrow \sqrt x</math> in y-Richtung gestaucht. | ||
| + | # Für <math>1 < a</math> wir der Graph der Wurzelfunktion <math>x \rightarrow \sqrt x</math> in y-Richtung gestreckt. | ||
| + | # Für negative <math>a</math> wird der Graph von 2. oder 3. an der y-Achse gespiegelt. | ||
| + | |||
| + | Die Definitionsmenge bleibt <math>R^+_0</math>. <br> | ||
| + | Für <math>a > 0</math> ist die Wertemenge <math>R^+_0</math>, für <math>a = 0</math> ist sie {0} und für <math>a < 0</math> <math>R^-_0</math> }} | ||
| + | |||
| + | Aufgabe 7: {{Lösung versteckt| | ||
| + | 1. Wie in Aufgabe 6!<br> | ||
| + | 2. Der Graph der Quadratwurzelfunktion wird um b in Richtung der y-Achse verschoben. <br> | ||
| + | Es ist <math>D = R^+_0</math> und <math>W = [b; \infty [</math> | ||
| + | |||
| + | 3. <math>a</math> bewirkt eine Stauchung für <math> 0 < a < 1</math> und eine Streckung für <math> a > 1</math>. <br> | ||
| + | <math>b</math> bewirkt, dass der Graph der Funktion mit dem Funktionsterm <math> a \sqrt x</math> um b in Richtung der y-Achse verschoben wird. <br> | ||
| + | Ist a negativ, so wird der Graph an der waagrechten Geraden <math> y = b</math> gespiegelt. <br> | ||
| + | 4. <math> D = R^+_0</math> und <math>W = [b; \infty[</math> für <math>a > 0</math> und <math>W = ]-\infty;b] </math> für <math>a < 0</math> | ||
| + | }} | ||
| + | |||
| + | Aufgabe 8: {{Lösung versteckt| | ||
| + | 1. Für <math> b > 0 </math> wird der Graph der Wurzelfunktion entlang der x-Achse nach links verschoben.<br> | ||
| + | Für <math> b < 0</math> wird der Graph der Wurzelfunktion entlang der x-Achse nach rechts verschoben.<br> | ||
| + | Die Nullstelle tritt bei <math> x = -b</math> auf. <br> | ||
| + | <math>D = [-b;\infty[ </math>, Wertemenge: <math>R^+_0</math> | ||
| + | |||
| + | 2. Für <math> 0 < a < 1</math> wird der Graph der Wurzelfunktion in y-Richtung gestaucht. | ||
| + | <br>Für <math> a > 1</math> wird der Graph in y-Richtung gestreckt. | ||
| + | <br>Ist <math> a < 0</math> so wird der Graph mit <math>|a|</math> an der y-Achse gespiegelt. | ||
| + | <br>Für a > 0 ist <math>D = R^+_0</math>, für a < 0 ist <math>D = R^-_0</math> | ||
| + | <br>Wertemenge: <math>R^+_0</math> | ||
| + | |||
| + | 4. <math>x = -\frac{b}{a}</math> | ||
| + | |||
| + | 5. Ist <math> a > 0</math> dann ist <math>D = [-\frac{b}{a};\infty[ </math> und ist <math> a < 0</math>, dann ist <math>D = ]-\infty;-\frac{b}{a}] </math>}} | ||
| + | |||
| + | Aufgabe 9: {{Lösung versteckt| | ||
| + | [[Datei:Wf_versch.jpg|400px]]<br> | ||
| + | a) <math>f</math>: Der Graph der Quadratwurzelfunktion wird um 2 entlang der x-Achse nach links verschoben.<br> | ||
| + | b) <math>g</math>: Der Graph der Quadratwurzelfunktion wird um 2 entlang der y-Achse nach oben verschoben.<br> | ||
| + | c) <math>h</math>: Der Graph der Quadratwurzelfunktion wird um 2 entlang der x-Achse nach rechts verschoben.<br> | ||
| + | d) <math>k</math>: Der Graph der Quadratwurzelfunktion wird um den Faktor 2 in y-Richtung gestreckt.<br> | ||
| + | e) <math>l</math>: Der Graph der Quadratwurzelfunktion wird um 2 entlang der y-Achse nach unten verschoben.<br> | ||
| + | f) <math>k</math>: Der Graph der Quadratwurzelfunktion wird um den Faktor 2 in y-Richtung gestaucht und dann an der x-Achse gespiegelt.}} | ||
| + | |||
| + | Aufgabe 10: {{Lösung versteckt| | ||
| + | # <math>D = [-5;5]</math> | ||
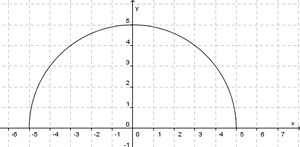
| + | # [[Datei:Halbkreis.jpg|300px]] | ||
| + | # Halbkreis | ||
| + | # Für einen Punkt P(x;y) auf dem Graphen gilt: <math> x^2 + y^2 = x^2 + (25 - x^2) = 25</math> unabhängig von x. Also hat jeder Punkt auf dem Graphen den Abstand 5 vom Ursprung. | ||
}} | }} | ||
---- | ---- | ||
| − | Zurück zu [[Wurzelfunktion_Einführung|Wurzelfunktion]] oder weiter mit [[Wurzelfunktion_Anwendungen|Anwendungen]] | + | Zurück zu [[Wurzelfunktion_Einführung|Wurzelfunktion]] oder weiter mit [[Wurzelfunktion_Anwendungen|Anwendungen]] oder mit [[Wurzelfunktionen_Eigenschaften|Weitere Eigenschaften]] |
Aktuelle Version vom 16. April 2017, 10:16 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen - Weitere Eigenschaften --- Die allgemeine Wurzelfunktion - Übungen und Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Bei den Übungen zur Wurzelfunktion lernst du weitere sich aus ihr ergebene Funktionen kennen.
|
Zeichne den Graphen der Funktionen Beschreibe mit Worten die besondere Lage dieser beiden Graphen zueinander. |
Neben der Quadratwurzelfunktion treten auch Funktionsterme der Art
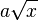 ,
,
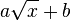 und
und
auf. Diese wirst du nun mit der Methode "Gruppenpuzzle" untersuchen.
Jede der folgenden Aufgabenstellungen (6, 7 und 8) wird von ein oder zwei Gruppen bearbeitet. Jedes Gruppenmitglied muss in der Lage sein, das Wissen weiterzugeben.
Überlegt gemeinsam, welche Informationen am wichtigsten sind und unbedingt in euren Mitschriften stehen sollten.
|
Im Applet ist der Graph der Wurzelfunktion Beschreibe, wie sich der Graph der Wurzelfunktion Wie wirkt sich die Änderung des Parameters |
|
Du betrachstest die Funktion 1. Variiere 3. Variiere nun a und b gleichzeitig und beobachte was passiert. |
|
Du betrachstest die Funktion 1. Was passiert, wenn du den Wert von |
Mischgruppen
Jede Mischgruppe besteht aus mindestens einer Expertin bzw. einem Experten zu den obigen drei Aufgaben. Die Expertinnen und Experten fassen das Wesentliche für die anderen zusammen. Gemeinsam werden anschließend die folgenden drei Aufgaben gelöst.
|
Skizziere und vergleiche die Graphen folgender Funktionen! Gib jeweils den Definitions- und Wertebereich an! |
|
Es ist die Funktion
|
|
a) Löse dieses Quiz. |
Präsentation der Ergebnisse - Staffellauf
Präsentiert nun eure Ergebnisse zu den Aufgaben 9 und 10 aus der Mischgruppe in Form eines Staffellaufes.
D.h.: Jede Teilaufgabe wird von einem/einer Schüler/in im Plenum vorgestellt.
Aufgabe 5: [Lösung anzeigen]
Aufgabe 6: [Lösung anzeigen]
Aufgabe 7: [Lösung anzeigen]
Aufgabe 8: [Lösung anzeigen]
Aufgabe 9: [Lösung anzeigen]
Aufgabe 10: [Lösung anzeigen]
Zurück zu Wurzelfunktion oder weiter mit Anwendungen oder mit Weitere Eigenschaften
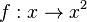 im Intervall [0;3] und den Graphen der Funktion
im Intervall [0;3] und den Graphen der Funktion 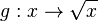 im Intervall [0;7] in ein Koordinatensystem.
im Intervall [0;7] in ein Koordinatensystem.
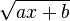
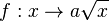 mit
mit  dargestellt.
dargestellt. .
.
 ändert für
ändert für
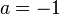
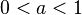
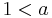
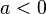
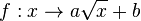 . Im folgenden Applet kannst du mit den Schiebereglern die Werte für
. Im folgenden Applet kannst du mit den Schiebereglern die Werte für 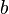 verändern.
verändern. 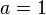 und
und 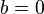 . Es ist der Graph der Quadratwurzelfunktion dargestellt.
. Es ist der Graph der Quadratwurzelfunktion dargestellt.
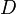 und die Wertemenge
und die Wertemenge 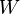 ?
?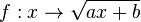 . Im folgenden Applet kannst du mit den Schiebereglern die Werte für
. Im folgenden Applet kannst du mit den Schiebereglern die Werte für 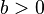 und
und 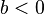 . Gib die Nullstellen an!
. Gib die Nullstellen an! 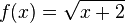
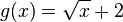
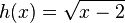
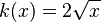
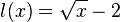
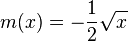
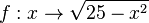 gegeben.
gegeben.
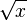 sqrt(x).
sqrt(x).
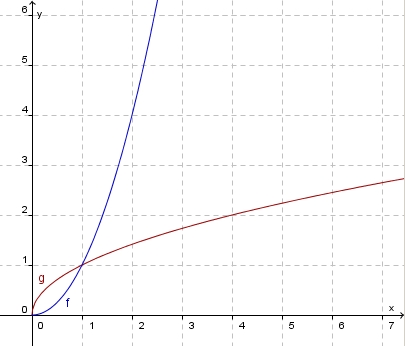
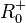 .
. 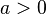 ist die Wertemenge
ist die Wertemenge 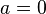 ist sie {0} und für
ist sie {0} und für 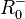
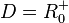 und
und 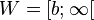
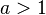 .
. 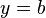 gespiegelt.
gespiegelt. ![W = ]-\infty;b]](/images/math/9/9/0/99039a54583ef87429a5932e628b81dd.png) für
für 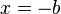 auf.
auf. 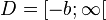 , Wertemenge:
, Wertemenge:  an der y-Achse gespiegelt.
an der y-Achse gespiegelt.
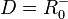
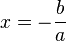
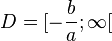 und ist
und ist ![D = ]-\infty;-\frac{b}{a}]](/images/math/2/c/f/2cfe464d0d1d2e691d026209a3879df9.png)
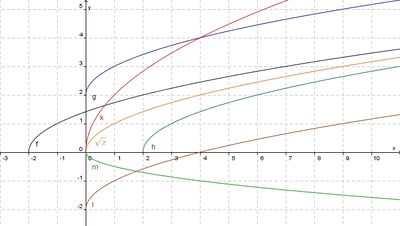
 : Der Graph der Quadratwurzelfunktion wird um 2 entlang der x-Achse nach links verschoben.
: Der Graph der Quadratwurzelfunktion wird um 2 entlang der x-Achse nach links verschoben.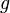 : Der Graph der Quadratwurzelfunktion wird um 2 entlang der y-Achse nach oben verschoben.
: Der Graph der Quadratwurzelfunktion wird um 2 entlang der y-Achse nach oben verschoben.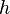 : Der Graph der Quadratwurzelfunktion wird um 2 entlang der x-Achse nach rechts verschoben.
: Der Graph der Quadratwurzelfunktion wird um 2 entlang der x-Achse nach rechts verschoben.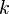 : Der Graph der Quadratwurzelfunktion wird um den Faktor 2 in y-Richtung gestreckt.
: Der Graph der Quadratwurzelfunktion wird um den Faktor 2 in y-Richtung gestreckt.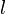 : Der Graph der Quadratwurzelfunktion wird um 2 entlang der y-Achse nach unten verschoben.
: Der Graph der Quadratwurzelfunktion wird um 2 entlang der y-Achse nach unten verschoben.![D = [-5;5]](/images/math/1/2/0/120287c752ac534bf003f2ea5f8fc0f6.png)
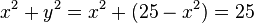 unabhängig von x. Also hat jeder Punkt auf dem Graphen den Abstand 5 vom Ursprung.
unabhängig von x. Also hat jeder Punkt auf dem Graphen den Abstand 5 vom Ursprung.

