Wurzelfunktion Umkehrfunktion: Unterschied zwischen den Versionen
| (49 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | [[ | + | [[Wurzelfunktion_Startseite|Startseite]] --- [[Wurzelfunktion_Einführung|Die Wurzelfunktion]] - [[Wurzelfunktion_Übungen_1|Übungen]] - [[Wurzelfunktion_Anwendungen|Anwendungen]] - [[Wurzelfunktionen_Eigenschaften|Weitere Eigenschaften]] --- [[Wurzelfunktion_allgemeine_Wurzelfunktion|Die allgemeine Wurzelfunktion]] - [[Wurzelfunktion_Übungen_2|Übungen und Anwendungen]] --- [[Wurzelfunktion_Umkehrfunktion|Die Wurzelfunktion als Umkehrfunktion]] |
| − | + | __NOCACHE__ | |
---- | ---- | ||
| − | [[Bild: | + | [[Bild:E_Quadrat1.jpg|right|163px]] |
| + | Nochmals zum Anfangsbeispiel: | ||
| + | Ein Quadrat mit Seitenlänge a hat den Flächeninhalt <math> A = a^2</math>.<br><br> | ||
| + | Wenn du von einem Quadrat den Flächeninhalt mit 9 FE kennst, wie lang ist dann die Seite <math>a</math>? Natürlich 3 LE.<br><br> | ||
| + | Es gilt also: <math> a = \sqrt {A}</math> | ||
| + | <br><br> | ||
| + | Ausgangspunkt war die Gleichung <math> A = a^2</math>. <br> | ||
| + | Diese wurde durch Anwenden der Umkehroperation nach <math>a</math> aufgelöst. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{Merke| | |
| − | + | Ordnet man jeder nicht negativen reellen Zahl <math>x</math> ihr Quadrat <math>x^2</math> zu, so erhält man die Quadratfunktion <math>f: x \rightarrow x^2</math> mit <math> x\in R^+_0</math>. | |
| − | + | ||
| − | + | Wird umgekehrt jeder nicht negativen reellen Zahl x ihre Quadratwurzel zugeordnet, so ist die Zuordnung <math> g: x \rightarrow \sqrt {x}</math> mit <math> x \in R^+_0</math> die Quadratwurzelfunktion oder Wurzelfunktion. | |
| + | <br> | ||
| + | |||
| + | Die Funktion <math>g</math> wird '''Umkehrfunktion''' der Funktion <math>f</math> genannt.<br> | ||
| + | Und anstelle von <math>g</math> wird auch <math> f^{-1}</math> geschrieben.<br> | ||
| + | <br>Die Wurzelfunktion <math> f^{-1}: x \rightarrow \sqrt {x}</math> mit <math> x \in R^+_0</math> ist die Umkehrfunktion zur Quadratfunktion <math>f: x \rightarrow x^2</math> mit <math> x\in R^+_0</math>. | ||
}} | }} | ||
| + | |||
| + | |||
| + | |||
| + | {{Arbeiten|NUMMER=26| ARBEIT= | ||
| + | In diesem Bild sind die Graphen der Funktionen <math>f: x \rightarrow x^2</math> mit <math> x\in R^+_0</math> und <math> g: x \rightarrow \sqrt {x}</math> mit <math> x \in R^+_0</math> dargestellt. | ||
| + | |||
| + | <center>[[Datei:Umk_funk_1.jpg]]</center> | ||
| + | |||
| + | Was fällt dir auf? | ||
| + | }} | ||
| + | |||
| + | |||
| + | Bisher hast du gelernt, dass die Funktionsgraphen von Umkehrfunktionen <math>f^{-1}</math> und ihre Funktion <math>f</math> symmetrisch zur Geraden y = x (1. Mediane) sind.<br> | ||
| + | Dieser Zusammenhang wird durch das [http://medienvielfalt.zum.de/images/7/7b/ArbeitsblattFaltbild.pdf Arbeitsblatt] verdeutlicht! | ||
| + | <br><br> | ||
| + | Jetzt lernt du, die Umkehrfunktion rechnerisch zu ermitteln.<br> | ||
| + | Gehe zum Beispiel von der Funktiongleichung <math>y = 2x + 4</math> aus.<br> | ||
| + | Vertausche in dieser Gleichung <math>x</math> und <math>y</math>: <math>x = 2y + 4</math><br><br> | ||
| + | Das Umformen dieser Gleichung nach <math>y</math> ergibt die Umkehrfunktion: <math>y = \frac{x-4}{2}</math> also ist <math>y = \frac{x}{2} - 2</math>. | ||
| + | <br><br>Dieses Verfahren zur Ermittlung der Umkehrfunktion kannst du auch auf Potenz- und Wurzelfunktionen anwenden. | ||
| + | |||
| + | |||
| + | {{Arbeiten|NUMMER=27| ARBEIT= | ||
| + | Ermittle | ||
| + | # graphisch | ||
| + | # rechnerisch<br> | ||
| + | die Umkehrfunktionen zu <math>f:x\rightarrow \sqrt{3x}</math> und <math>g: x\rightarrow x^2 + 3</math> | ||
| + | }} | ||
| + | |||
| + | |||
| + | {{Merke| | ||
| + | Für jede natürliche Zahl <math> n </math> ist die Potenzfunktion <math> f: x \rightarrow x^n</math> mit <math> x \in R^+_0</math> umkehrbar.<br> | ||
| + | Die Umkehrfunktion <math> f^{-1}</math> lautet: <math> f^{-1}: x \rightarrow \sqrt[n]{x}</math> mit <math> x \in R^+_0</math>. Sie heißt n-te Wurzelfunktion. | ||
| + | <br><br> | ||
| + | Die n-te Wurzelfunktion <math> f^{-1}: x \rightarrow \sqrt[n]{x}</math> mit <math> x \in R^+_0</math> kannst du auch als Potenzfunktion betrachten, deren Exponent ein Stammbruch ist. | ||
| + | <br>Dann gilt: <math> f^{-1}: x \rightarrow x^{\frac{1}{n}}</math> mit <math> x \in R^+_0</math> und <math> n \in N</math>. | ||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | Aufgabe 26: {{Lösung versteckt|1= | ||
| + | Die Graphen von f und g sind symmetrisch zur Gerade y = x (1. Mediane). | ||
| + | }} | ||
| + | |||
| + | Aufgabe 27: {{Lösung versteckt| | ||
| + | # Spiegeln an der Geraden <math> y = x</math> | ||
| + | # <math>f:x\rightarrow \sqrt{3x}</math>:<br> | ||
| + | :In der Gleichung <math> y = \sqrt{3x}</math> vertauscht man x und y und löst dann nach y aufl. Man erhält <math> x = \sqrt{3y}</math> und dann <math>y = \frac{x^2}{3}</math>.<br> Die Umkehrfunktion lautet <math> f^{-1}: x \rightarrow \frac{x^2}{3}</math>. <br> | ||
| + | :Die Defintionsmenge der Umkehrfunktion ist <math>D = R^+_0</math>. | ||
| + | |||
| + | :<math>g: x\rightarrow x^2 + 3</math>:<br> | ||
| + | :Zuerst muss man die Definitionsmenge von <math>g</math> auf <math>R^+_0</math> einschränken.<br> | ||
| + | :In der Gleichung <math> y = x^2 + 3</math> x und y vertauschen und dann nach y auflösen. Man erhält <math> x = y^2 + 3</math> und dann <math>y = \sqrt{x-3}</math>.<br> Die Umkehrfunktion lautet <math> g^{-1}: x \rightarrow \sqrt{x-3}</math>. <br> | ||
| + | :Die Defintionsmenge der Umkehrfunktion ist <math>D = R^+_0</math>. | ||
| + | |||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | '''Bemerkung: ''' | ||
| + | |||
| + | Alle Potenzfunktionen sind für <math>x \in R</math> definiert. Dies kann man bei der Bildung von Umkehrfunktionen nicht immer aufrecht erhalten. Potenzfunktionen mit ungeraden Exponenten kann man auch für <math>x \in R^-</math> umkehren, bei geraden Exponenten geht dies nicht. Wenn du hierzu mehr wissen willst, lies die folgenden Seiten: | ||
| + | |||
| + | [http://www.mathematik.net/Pot-fkt/Pw4s10.htm Potenzfunktionen mit geraden Exponenten haben eine Umkehrrelation]<br> | ||
| + | [http://www.mathematik.net/Pot-fkt/Pw4s13.htm So findet man bei Potenzfunktionen mit geraden Exponenten die Umkehrfunktion] | ||
Aktuelle Version vom 16. April 2017, 10:02 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen - Weitere Eigenschaften --- Die allgemeine Wurzelfunktion - Übungen und Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Nochmals zum Anfangsbeispiel:
Ein Quadrat mit Seitenlänge a hat den Flächeninhalt 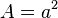 .
.
Wenn du von einem Quadrat den Flächeninhalt mit 9 FE kennst, wie lang ist dann die Seite  ? Natürlich 3 LE.
? Natürlich 3 LE.
Es gilt also: 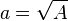
Ausgangspunkt war die Gleichung 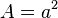 .
.
Diese wurde durch Anwenden der Umkehroperation nach  aufgelöst.
aufgelöst.
|
Ordnet man jeder nicht negativen reellen Zahl Wird umgekehrt jeder nicht negativen reellen Zahl x ihre Quadratwurzel zugeordnet, so ist die Zuordnung Die Funktion |
|
In diesem Bild sind die Graphen der Funktionen 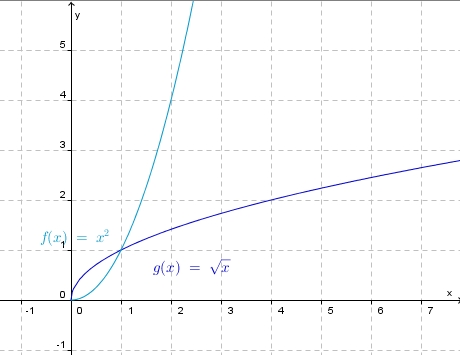 Was fällt dir auf? |
Bisher hast du gelernt, dass die Funktionsgraphen von Umkehrfunktionen 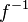 und ihre Funktion
und ihre Funktion  symmetrisch zur Geraden y = x (1. Mediane) sind.
symmetrisch zur Geraden y = x (1. Mediane) sind.
Dieser Zusammenhang wird durch das Arbeitsblatt verdeutlicht!
Jetzt lernt du, die Umkehrfunktion rechnerisch zu ermitteln.
Gehe zum Beispiel von der Funktiongleichung 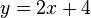 aus.
aus.
Vertausche in dieser Gleichung  und
und 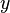 :
: 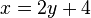
Das Umformen dieser Gleichung nach 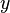 ergibt die Umkehrfunktion:
ergibt die Umkehrfunktion:  also ist
also ist 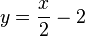 .
.
Dieses Verfahren zur Ermittlung der Umkehrfunktion kannst du auch auf Potenz- und Wurzelfunktionen anwenden.
|
Ermittle
die Umkehrfunktionen zu |
|
Für jede natürliche Zahl |
Aufgabe 26:
Aufgabe 27:
- Spiegeln an der Geraden
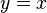
-
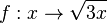 :
:
- In der Gleichung
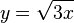 vertauscht man x und y und löst dann nach y aufl. Man erhält
vertauscht man x und y und löst dann nach y aufl. Man erhält 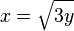 und dann
und dann 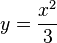 .
.
Die Umkehrfunktion lautet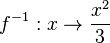 .
.
- Die Defintionsmenge der Umkehrfunktion ist
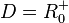 .
.
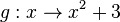 :
:
- Zuerst muss man die Definitionsmenge von
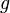 auf
auf 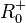 einschränken.
einschränken.
- In der Gleichung
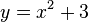 x und y vertauschen und dann nach y auflösen. Man erhält
x und y vertauschen und dann nach y auflösen. Man erhält 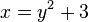 und dann
und dann 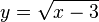 .
.
Die Umkehrfunktion lautet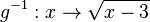 .
.
- Die Defintionsmenge der Umkehrfunktion ist
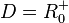 .
.
Bemerkung:
Alle Potenzfunktionen sind für 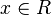 definiert. Dies kann man bei der Bildung von Umkehrfunktionen nicht immer aufrecht erhalten. Potenzfunktionen mit ungeraden Exponenten kann man auch für
definiert. Dies kann man bei der Bildung von Umkehrfunktionen nicht immer aufrecht erhalten. Potenzfunktionen mit ungeraden Exponenten kann man auch für 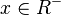 umkehren, bei geraden Exponenten geht dies nicht. Wenn du hierzu mehr wissen willst, lies die folgenden Seiten:
umkehren, bei geraden Exponenten geht dies nicht. Wenn du hierzu mehr wissen willst, lies die folgenden Seiten:
Potenzfunktionen mit geraden Exponenten haben eine Umkehrrelation
So findet man bei Potenzfunktionen mit geraden Exponenten die Umkehrfunktion

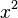 zu, so erhält man die Quadratfunktion
zu, so erhält man die Quadratfunktion 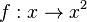 mit
mit  .
.
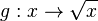 mit
mit 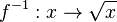 mit
mit 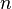 ist die Potenzfunktion
ist die Potenzfunktion 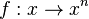 mit
mit ![f^{-1}: x \rightarrow \sqrt[n]{x}](/images/math/4/3/7/437f5d3ef49490d0b3699c6a229bb421.png) mit
mit 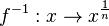 mit
mit 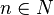 .
.

