Quadratische Funktionen 2 Einfluss von a: Unterschied zwischen den Versionen
| (8 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | Zurück zu [[Quadratische_Funktionen_2_-_Allgemeine_quadratische_Funktion|'''6. Allgemeine quadratische Funktion''']] | ||
| + | |||
| + | ---- | ||
| + | __NOCACHE__ | ||
| + | |||
{| | {| | ||
| | | | ||
| − | Wir betrachten nun den Einfluss von <math> \ a </math> in <math> x \rightarrow a x^2 </math>. | + | Wir betrachten nun den Einfluss von <math> \ a </math> in <math>f: x \rightarrow a x^2 </math>. |
| + | : | ||
: | : | ||
| − | |||
{{Arbeiten|NUMMER=A1|ARBEIT = | {{Arbeiten|NUMMER=A1|ARBEIT = | ||
| − | <ggb_applet height="500" width="700" | + | <center><ggb_applet height="500" width="700" |
| − | filename="Qf-a.ggb" /> | + | filename="Qf-a.ggb" /></center> |
# Mit dem Schieberegler kannst du den Wert von <math> \ a </math> ändern. <br> | # Mit dem Schieberegler kannst du den Wert von <math> \ a </math> ändern. <br> | ||
| Zeile 51: | Zeile 56: | ||
---- | ---- | ||
| − | Aufgabe | + | '''Aufgabe A1:''' {{Lösung versteckt| |
Man erhält den Graph der Funktion <math>f: x \rightarrow a x^2</math> | Man erhält den Graph der Funktion <math>f: x \rightarrow a x^2</math> | ||
| Zeile 63: | Zeile 68: | ||
}} | }} | ||
| − | {{Lösung versteckt| | + | '''Aufgabe A2:''' {{Lösung versteckt|1= |
Hier genügt es, wenn du diese Aufgabe mit Hilfe von Plausibilitätsüberlegungen gelöst hast. Eine formale Begründung war nicht notwendig. | Hier genügt es, wenn du diese Aufgabe mit Hilfe von Plausibilitätsüberlegungen gelöst hast. Eine formale Begründung war nicht notwendig. | ||
Eine mögliche formale Begründung: | Eine mögliche formale Begründung: | ||
| − | <math>ax^2 = 0 mit a\neq | + | <math>ax^2 = 0</math> mit <math>a\neq 0</math> <math>\Leftrightarrow x^2 = 0 </math> d.h. die Nullstellen bleiben gleich. <br> |
| − | + | ||
| − | \Leftrightarrow | + | |
Ferner wird jeder Funktionswert mit dem gleichen Faktor multipliziert. Ist der Betrag dieses Faktors größer als 1, so wird der Graph in Richtung der y-Achse um diesen Faktor gestreckt, ist er kleiner als 1, so wird er entsprechend gestaucht. Ist der Faktor negativ, so wird der Graph zusätzlich an der x-Achse gespiegelt. | Ferner wird jeder Funktionswert mit dem gleichen Faktor multipliziert. Ist der Betrag dieses Faktors größer als 1, so wird der Graph in Richtung der y-Achse um diesen Faktor gestreckt, ist er kleiner als 1, so wird er entsprechend gestaucht. Ist der Faktor negativ, so wird der Graph zusätzlich an der x-Achse gespiegelt. | ||
}} | }} | ||
| Zeile 78: | Zeile 81: | ||
<span style="background-color:yellow;">Hefteintrag:</span> Beachte, dass in der Lösung zur Aufgabe A1 ein Hefteintrag "versteckt" ist! | <span style="background-color:yellow;">Hefteintrag:</span> Beachte, dass in der Lösung zur Aufgabe A1 ein Hefteintrag "versteckt" ist! | ||
| + | |||
| + | ---- | ||
| + | Zurück zu [[Quadratische_Funktionen_2_-_Allgemeine_quadratische_Funktion|'''6. Allgemeine quadratische Funktion''']] | ||
Aktuelle Version vom 9. Dezember 2020, 12:28 Uhr
Zurück zu 6. Allgemeine quadratische Funktion
|
Wir betrachten nun den Einfluss von
|
|
|
Aufgabe A1:
Man erhält den Graph der Funktion 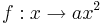
aus dem Graph der Quadratfunktion 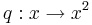 durch Streckung oder Stauchung in Richtung der y-Achse.
durch Streckung oder Stauchung in Richtung der y-Achse.
Genauer:
- Ist der Betrag von a größer als eins, so wird der Graph der Sinusfunktion in y-Richtung mit dem Faktor Betrag von a gestreckt.
- Ist der Betrag von a kleiner als eins und positiv, so wird der Graph der Sinusfunktion in y-Richtung mit dem Faktor Betrag von a gestaucht.
- Falls a negativ ist, so wird der Graph zusätzlich an der x-Achse gespiegelt.
Aufgabe A2:
Hier genügt es, wenn du diese Aufgabe mit Hilfe von Plausibilitätsüberlegungen gelöst hast. Eine formale Begründung war nicht notwendig.
Eine mögliche formale Begründung:
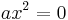 mit
mit 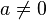
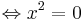 d.h. die Nullstellen bleiben gleich.
d.h. die Nullstellen bleiben gleich.
Hefteintrag: Beachte, dass in der Lösung zur Aufgabe A1 ein Hefteintrag "versteckt" ist!
Zurück zu 6. Allgemeine quadratische Funktion
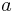 in
in 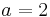 ein. Wie ändert sich der Graph?
ein. Wie ändert sich der Graph? 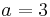 und
und 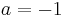 sowie
sowie 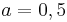 auf den Graphen auswirken und überprüfe deine Vermutung.
auf den Graphen auswirken und überprüfe deine Vermutung. 
