Quadratische Funktionen 2 Didaktischer Kommentar: Unterschied zwischen den Versionen
(→Hefteintrag) |
(→Unterrichtsformen) |
||
| (22 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | '''Lernpfad Quadratische Funktionen_2'''<br> | + | <big>'''Lernpfad Quadratische Funktionen_2'''</big><br> |
| − | + | ||
---- | ---- | ||
| Zeile 7: | Zeile 7: | ||
---- | ---- | ||
| + | |||
| + | =Kurzübersicht= | ||
| + | |||
| + | {| | ||
| + | | | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | | ||
| + | Schulstufe | ||
| + | |colspan="3"| 5. Schulstufe in Österreich bzw. 9. Jahrgangsstufe in Deutschland | ||
| + | |- | ||
| + | | | ||
| + | Unterrichtsfächer | ||
| + | || | ||
| + | Mathematik, Mathematik und Physik, Alltagsanwendungen | ||
| + | |- | ||
| + | | | ||
| + | Dauer | ||
| + | || | ||
| + | 8 Stunden | ||
| + | |- | ||
| + | | | ||
| + | Technische Voraussetzungen | ||
| + | |colspan="3"| | ||
| + | Internet und Java, YouTube für Videos | ||
| + | |- | ||
| + | | | ||
| + | Medien | ||
| + | || | ||
| + | Java-Applets, GeoGebra, Bilder, interaktive Tests | ||
| + | |- | ||
| + | | | ||
| + | Lernziele | ||
| + | || | ||
| + | * Übersetzen von einer Realsituation in ein mathematisches Modell | ||
| + | * Parabeln als Graphen quadratischer Funktionen identifizieren | ||
| + | * Bei quadratischen Funktionen zwischen den Darstellungsformen Graph, Tabelle und Formel wechseln | ||
| + | * Parameter variieren und die Auswirkung dieser Variation beschreiben | ||
| + | * Bestimmen der Parameter bzw. des Funktionsterms in verschiedenen Darstellungen der quadratischen Funktionen | ||
| + | |- | ||
| + | | | ||
| + | Kompetenzen | ||
| + | || | ||
| + | Operieren, Interpretieren, Kommunizieren, Argumentieren, Dokumentieren, Transferieren | ||
| + | |||
| + | |- | ||
| + | | | ||
| + | Methodik | ||
| + | || | ||
| + | Gruppenarbeit, Arbeit in Expertenteams oder Pferdestall, Lernen an Stationen | ||
| + | |- | ||
| + | | | ||
| + | Autoren | ||
| + | |colspan="3"| | ||
| + | Reinhard Schmidt, Christian Schmidt, Maria Eirich, Andrea Schellmann (2009), überarbeitet von Karl Haberl (2011) | ||
| + | |} | ||
| + | |||
=Grundsätzliches= | =Grundsätzliches= | ||
Dieser Lernpfad bietet einen Einstieg in das Thema "Quadratische Funktionen". Die Einführung erfolgt am Beispiel des Bremsweges eines Autos, genauer gesagt anhand des Zusammenhangs zwischen der Geschwindigkeit eines Autos und der Länge seines Bremsweges.<br> | Dieser Lernpfad bietet einen Einstieg in das Thema "Quadratische Funktionen". Die Einführung erfolgt am Beispiel des Bremsweges eines Autos, genauer gesagt anhand des Zusammenhangs zwischen der Geschwindigkeit eines Autos und der Länge seines Bremsweges.<br> | ||
| − | Nachdem auf diese Weise der Begriff der reinquadratischen Funktion erarbeitet worden ist, | + | Nachdem auf diese Weise der Begriff der reinquadratischen Funktion erarbeitet worden ist, soll zuerst die Scheitelform einer quadratischen Funktion anhand der Köln-Arena erarbeitet werden. <br> |
In der Scheitelform der quadratischen Funktion kommen Parameter vor, deren Einfluss auf den Graphen erkundet wird.<br> | In der Scheitelform der quadratischen Funktion kommen Parameter vor, deren Einfluss auf den Graphen erkundet wird.<br> | ||
Die Scheitelform einer quadratischen Funktion ist eine allgemeine Beschreibung, die auch in der Form der Funktionegleichung <math> f(x) = a x^2 + bx + c</math> beschreibbar ist.<br> | Die Scheitelform einer quadratischen Funktion ist eine allgemeine Beschreibung, die auch in der Form der Funktionegleichung <math> f(x) = a x^2 + bx + c</math> beschreibbar ist.<br> | ||
| Zeile 50: | Zeile 107: | ||
=Sozialformen und Methodik= | =Sozialformen und Methodik= | ||
| + | ==Arbeitsformen== | ||
Als Sozialform wird für die meisten Teile des Lernpfades Partnerarbeit vorgeschlagen.<br> | Als Sozialform wird für die meisten Teile des Lernpfades Partnerarbeit vorgeschlagen.<br> | ||
Auf diese Weise wird gewährleistet, dass einerseits der zu erarbeitende Stoff selbstständig entdeckt, andererseits aber mit dem Partner argumentiert und kommuniziert wird. Das zu Lernende kann dadurch noch nachhaltiger durchdrungen | Auf diese Weise wird gewährleistet, dass einerseits der zu erarbeitende Stoff selbstständig entdeckt, andererseits aber mit dem Partner argumentiert und kommuniziert wird. Das zu Lernende kann dadurch noch nachhaltiger durchdrungen | ||
| Zeile 61: | Zeile 119: | ||
Eine andere Möglichkeit als Expertengruppen bietet der [[Trigonometrische_Funktionen_2/Einfluss_der_Parameter/Arbeiten_im_Pferdestall|Pferdestall]]. | Eine andere Möglichkeit als Expertengruppen bietet der [[Trigonometrische_Funktionen_2/Einfluss_der_Parameter/Arbeiten_im_Pferdestall|Pferdestall]]. | ||
| + | |||
| + | Das Arbeiten in Expertengruppen und Pferdestall sind ausführlich im [[Trigonometrische_Funktionen_2/Didaktischer_Kommentar#Methodik|didaktischen Kommentar des Lernpfad trigonometrische Funktionen_2]] beschrieben. | ||
| + | |||
| + | ==Unterrichtsformen== | ||
| + | Bewusst wurde der Lernpfad linear angelegt, d.h. man kann ihn von Station 1 bis 9 der Reihe nach bearbeiten, da die auftretenden Probleme sich natürlich ergeben und gelöst werden können. Daher wurde ebenso bewusst die Scheitelform in den Lernpfad mit aufgenommen, da hier der Einfluss der Parameter sehr einfach zu erkennen ist und die Auswirkungen auf den Graphen intuitiv sind. Weiterhin ist am Ende der Seite stets ein Links auf die nächste Seite, die beim linearen Bearbeiten des Lernpfad folgt. | ||
| + | <center>[[Datei:Qf-ablauf-llinear.jpg|300px]]</center> | ||
| + | |||
| + | '''Lernen an Stationen'''<br> | ||
| + | Man kann den Lernpfad aber auch als "Lernen an Stationen" auffassen, und den SchülerInnen einen Lernplan mit den Stationen 1 bis 9 mitgeben, auf dem sie notieren, was schon bearbeitet wurde. Hier ist anzugeben, dass die Stationen 1 bis 3 und 7 bis 8 absolut verbindlich sind und die Stationen 4 bis 6 und 8 fakultativ bearbeitet werden können. Mögliche Anfangsstationen sind 1 oder 4 oder 7. | ||
| + | |||
| + | Das Arbeitsblatt für SchülerInnen kann [http://wikis.zum.de/medienvielfalt/images/1/17/QF-Lernen_an_Stationen.pdf hier] heruntergeladen und dann ausgedruckt werden. | ||
| + | |||
| + | '''Pflichtstationen'''<br> | ||
| + | Die Scheitelform wurde bewusst mit in den Lernpfad aufgenommen, da man hier schon auch für weitere Funktionen die Auswirkung der Parameter für die Verschiebungen in x- und y-Richtung einfach erkennen kann. Dies kommt den SchülerInnen bei anderen Lernpfaden wie den trigonometrischen Funktionen einfach zu gute.<br> | ||
| + | Will man die Scheitelform nicht bearbeiten, lässt man Station 5 und 6 aus und geht gleich zu Station 7. Eine Behandlung der Scheitelform ist auch am Ende des Lernpfades möglich.<br> | ||
| + | Am Ende der Station 4 ist daher auch ein Sprung zu Station 7 möglich.<br> | ||
| + | Verpflichtend zu bearbeiten sind auf jeden Fall die Stationen 1 bis 3 und 7 bis 8. Die anderen Stationen 4 bis 6 und 8 werden SchülerInnen angeboten, die bereits fertig sind oder mehr bearbeiten wollen. | ||
| + | <center>[[Datei:Qf-ablauf-pflicht.jpg|250px]]</center> | ||
| + | |||
| + | Es ist auch möglich nach der Einführung <br> | ||
| + | ''1. Bremsweg - 2. Unterschiedliche Straßenverhältnisse - 3. Übungen 1'' <br> | ||
| + | zuerst die allgemeine quadratische Funktion <br> | ||
| + | ''7. Allgemeine quadratische Funktion - 8. Übungen 3'' <br> | ||
| + | und danach die Scheitelform<br> | ||
| + | ''4. Köln-Arena - 5. Einfluss der Parameter in der Scheitelform - 6. Übungen 2'' <br> | ||
| + | zu behandeln. | ||
| + | <center>[[Datei:Qf-ablauf-entscheidung.jpg|600px]]</center> | ||
=Genderaspekte= | =Genderaspekte= | ||
| − | Mit Blick auf die Genderproblematik wurde stets darauf geachtet, dass sie Mädchen und Jungen gleichermaßen ansprechen. Auch wenn der Bremsweg vielleicht Jungen mehr anspricht, so ist es ebenso für Mädchen interessant und wichtig. | + | Mit Blick auf die Genderproblematik wurde stets darauf geachtet, dass sie Mädchen und Jungen gleichermaßen ansprechen. Auch wenn der Bremsweg vielleicht Jungen mehr anspricht, so ist es ebenso für Mädchen interessant und wichtig. Jungen und Mädchen sind in einem Alter, in dem demnächst der Führerschein ansteht, daher ist diese Problematik für beide ausgesprochen hilfreich. Die weitere Hinführung über die Köln-Arena zu den allgemeinen quadratischen Funktionen ist, da dann auch rein mathematische Inhalte durch interaktive Übungen erarbeitet werdem, die durch den hohen Experimentieranteil sowohl Mädchen als auch Burschen animieren sollen, für beide Geschlechter gleich gut geeignet. . Durch das Zusammenspiel von Bildbeispielen und Interaktivität wurden die abstrakten Modelle alltagsverständlich heruntergebrochen.<br> |
| − | + | Die Übungen sind, da die Aufgaben hauptsächlich mathematisch orientiert sind, für Jungen und Mädchen gleich geeignet sind. Da die Aufgabenseite am Schluss fakultativ bearbeitet werden kann, sind hier vielleicht wieder mehr die Jungen mit dem Anhalteweg angesprochen. Die Aufgabe ist aber gleichermaßen aus den schon oben erwähnten Gründen für Mädchen ebenso gut geeignet. | |
Durch die verschiedene vorgeschlagene Lernmethoden werden unterschiedliche Lernprozesse ermöglicht wie zum Beispiel kooperatives und integratives Lernen, welche beide Geschlechter gleichermaßen ansprechen. | Durch die verschiedene vorgeschlagene Lernmethoden werden unterschiedliche Lernprozesse ermöglicht wie zum Beispiel kooperatives und integratives Lernen, welche beide Geschlechter gleichermaßen ansprechen. | ||
| Zeile 85: | Zeile 170: | ||
Zu fast allen Aufgaben sind Lösungen angegeben. Die SchülerInnen haben so die Möglichkeit, ihre Antworten selbst zu kontrollieren. | Zu fast allen Aufgaben sind Lösungen angegeben. Die SchülerInnen haben so die Möglichkeit, ihre Antworten selbst zu kontrollieren. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | Zurück zur [[Quadratische_Funktionen_2|'''Startseite: Quadratische Funktionen''']] | ||
Aktuelle Version vom 10. September 2011, 07:31 Uhr
Lernpfad Quadratische Funktionen_2
Zurück zur Startseite: Quadratische Funktionen
Inhaltsverzeichnis |
Kurzübersicht
GrundsätzlichesDieser Lernpfad bietet einen Einstieg in das Thema "Quadratische Funktionen". Die Einführung erfolgt am Beispiel des Bremsweges eines Autos, genauer gesagt anhand des Zusammenhangs zwischen der Geschwindigkeit eines Autos und der Länge seines Bremsweges. KompetenzenEingangskompetenzen• Bei linearen Funktionen zwischen den Darstellungsformen Graph, Tabelle und Formel wechseln ZielkompetenzenIn diesem Lernpfad soll Neues erlernt werden. Daher stehen hauptsächlich die Kompetenzen Operieren und Interpretieren im Vordergrund. Je nach eingesetzter Methode, wie Gruppenarbeit, Expertenteams, Pferdestall sind auch die Kompetenzen Argumentieren und Kommunizieren angesprochen. Da die SchülerInnen selbstständig Hefteinträge erstellen müssen, dokumentieren sie auch. Insgesamt werden alle Handlungskompetenzen Darstellen/Modellieren - Rechnen/Operieren - Interpretieren - Argumentieren/Begründen - Problemlösen - Transferieren - Dokumentieren - Kommunizieren genutzt, gefordert und gefördert Didaktischer HintergrundIntention des Lernpfades ist es, einen motivierenden, zugleich aber auch anspruchsvollen Einstieg in das Thema Quadratische Funktionen anzubieten. Insbesondere soll von vorneherein der Einfluss von Parametern in den Blick genommen werden – im klassischen „Tafelunterricht“ wäre dies an so früher Stelle wohl nur schwerlich möglich. Im kompletten Lernpfad steht die Selbsttätigkeit der Schülerinnen und Schüler im Vordergrund. Im Idealfall muss die Lehrperson nur in Ausnahmefällen in den eigentlichen Lernprozess eingreifen. Sozialformen und MethodikArbeitsformenAls Sozialform wird für die meisten Teile des Lernpfades Partnerarbeit vorgeschlagen. Für die Untersuchung des Einflusses der Parameter a,d,e bei der Scheitelform bzw. a,b,c bei der allgemeinen Form der quadratischen Funktionen können Expertengruppen gebildet werden.
Eine andere Möglichkeit als Expertengruppen bietet der Pferdestall. Das Arbeiten in Expertengruppen und Pferdestall sind ausführlich im didaktischen Kommentar des Lernpfad trigonometrische Funktionen_2 beschrieben. UnterrichtsformenBewusst wurde der Lernpfad linear angelegt, d.h. man kann ihn von Station 1 bis 9 der Reihe nach bearbeiten, da die auftretenden Probleme sich natürlich ergeben und gelöst werden können. Daher wurde ebenso bewusst die Scheitelform in den Lernpfad mit aufgenommen, da hier der Einfluss der Parameter sehr einfach zu erkennen ist und die Auswirkungen auf den Graphen intuitiv sind. Weiterhin ist am Ende der Seite stets ein Links auf die nächste Seite, die beim linearen Bearbeiten des Lernpfad folgt.  Lernen an Stationen Das Arbeitsblatt für SchülerInnen kann hier heruntergeladen und dann ausgedruckt werden. Pflichtstationen  Es ist auch möglich nach der Einführung 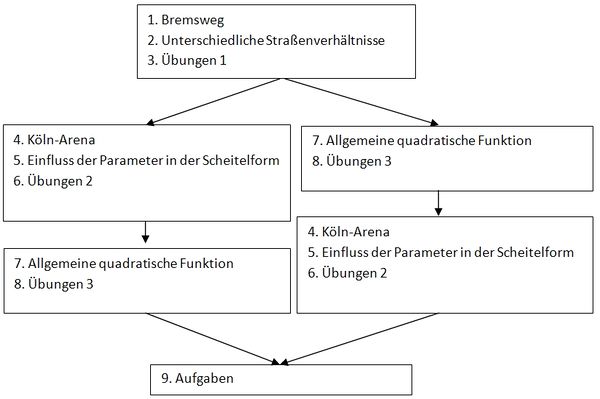 GenderaspekteMit Blick auf die Genderproblematik wurde stets darauf geachtet, dass sie Mädchen und Jungen gleichermaßen ansprechen. Auch wenn der Bremsweg vielleicht Jungen mehr anspricht, so ist es ebenso für Mädchen interessant und wichtig. Jungen und Mädchen sind in einem Alter, in dem demnächst der Führerschein ansteht, daher ist diese Problematik für beide ausgesprochen hilfreich. Die weitere Hinführung über die Köln-Arena zu den allgemeinen quadratischen Funktionen ist, da dann auch rein mathematische Inhalte durch interaktive Übungen erarbeitet werdem, die durch den hohen Experimentieranteil sowohl Mädchen als auch Burschen animieren sollen, für beide Geschlechter gleich gut geeignet. . Durch das Zusammenspiel von Bildbeispielen und Interaktivität wurden die abstrakten Modelle alltagsverständlich heruntergebrochen. Durch die verschiedene vorgeschlagene Lernmethoden werden unterschiedliche Lernprozesse ermöglicht wie zum Beispiel kooperatives und integratives Lernen, welche beide Geschlechter gleichermaßen ansprechen. MedienDer vorliegende Lernpfad wurde bewusst nicht im starren HTML-, sondern im dynamischen Wiki-Format angelegt, damit er beständig optimiert und angepasst werden kann. Sicherung des GelerntenDa im Lernpfad zunächst reinquadratische, später aber auch allgemeine quadratische Funktionen thematisiert werden, wird die Sicherung des Gelernten an drei Stellen in Form von Übungsseiten in den Lernpfad integriert. HefteintragEs ist sinnvoll, dass die SchülerInnen nach dem Bearbeiten des Lernpfades über Notizen verfügen, anhand derer sie das Gelernte wiederholen können. Deshalb wurden im gesamten Lernpfad Hefteinträge integriert. Oftmals sind die entsprechenden Texte gelb hinterlegt und sollen von den SchülerInnen übernommen werden. Dabei empfiehlt es sich aus Gründen der Übersichtlichkeit das Heft im Querformat zu verwenden. Hinweise zum Hefteintrag sind für die SchülerInnen zusätzlich im Lernpfad integriert. Aufgaben und LösungenZu fast allen Aufgaben sind Lösungen angegeben. Die SchülerInnen haben so die Möglichkeit, ihre Antworten selbst zu kontrollieren. Zurück zur Startseite: Quadratische Funktionen |
||||||||||||||||||||||||
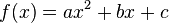 beschreibbar ist.
beschreibbar ist.
