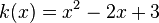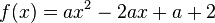Quadratische Funktionen 2 - Aufgaben: Unterschied zwischen den Versionen
(→Weiterführende Links) |
(→Weiterführende Links) |
||
| (7 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | ||
| − | [[ | + | [[Quadratische_Funktionen_2_Startseite|'''Startseite''']] - [[Quadratische_Funktionen_2_-_Bremsweg|'''1. Bremsweg''']] - [[Quadratische_Funktionen_2_-_Bremsbeschleunigung|'''2. Unterschiedliche Straßenverhältnisse''']] - [[Quadratische_Funktionen_2_-_Übungen1|'''3. Übungen 1''']] - [[Quadratische_Funktionen_2_-_Köln-Arena|'''4. Köln-Arena''']] - [[Quadratische_Funktionen_2_-_Einfluss_der_Parameter|'''5. Einfluss der Parameter in der Scheitelform''']] - <br>[[Quadratische_Funktionen_2_-_Übungen2|'''6. Übungen 2''']] - [[Quadratische_Funktionen_2_-_Allgemeine_quadratische_Funktion|'''7. Allgemeine quadratische Funktion''']] - [[Quadratische_Funktionen_2_-_Übungen3|'''8. Übungen 3''']] - [[Quadratische_Funktionen_2_-_Aufgaben|'''9. Aufgaben''']] |
</div> | </div> | ||
| + | __NOCACHE__ | ||
| − | + | Hier lernst du, wenn du noch Lust hast, einiges über den Anhalteweg eines Autos, Springbrunnen, ... und du kannst noch üben. | |
| − | Hier lernst du, wenn du noch Lust hast, einiges über den Anhalteweg eines Autos. | + | |
== Der Anhalteweg == | == Der Anhalteweg == | ||
| Zeile 61: | Zeile 61: | ||
<br /> | <br /> | ||
| + | |||
| + | Löse mit diesem Applet indem du experimentierst und die Werte abliest folgende Aufgabe. | ||
{{Arbeiten| | {{Arbeiten| | ||
| Zeile 83: | Zeile 85: | ||
}} | }} | ||
| − | Den Einfluss der verschiedenen Faktoren auf die Länge des Anhalteweges kannst du auch mit [http:// | + | Den Einfluss der verschiedenen Faktoren auf die Länge des Anhalteweges kannst du auch mit [http://home.edvsz.fh-osnabrueck.de/~ludemann/tmp/Physik/java/physlets.www.zum.de/physlet/applets/hirsch.html diesem Applet] untersuchen. |
| Zeile 254: | Zeile 256: | ||
| width="50%" style="vertical-align:top" | | | width="50%" style="vertical-align:top" | | ||
<div style="margin:0; border:0px solid #dfdfdf; padding: 0em 1em 1em 1em; align:left;"> | <div style="margin:0; border:0px solid #dfdfdf; padding: 0em 1em 1em 1em; align:left;"> | ||
| − | Bestimme die Gleichungen der abgebildeten Parabeln. Mache einen günstigen Ansatz für den Funktionsterm!<br> | + | 1. Bestimme die Gleichungen der abgebildeten Parabeln. Mache einen günstigen Ansatz für den Funktionsterm!<br> |
Gib den Scheitel der Parabeln an. | Gib den Scheitel der Parabeln an. | ||
| Zeile 273: | Zeile 275: | ||
<!-- linke Spalte: Zwei div-Container --> | <!-- linke Spalte: Zwei div-Container --> | ||
<div style="margin: 0; margin-right:10px; border: 0px solid #dfdfdf; padding: 0em 1em 1em 1em; align:left;"> | <div style="margin: 0; margin-right:10px; border: 0px solid #dfdfdf; padding: 0em 1em 1em 1em; align:left;"> | ||
| − | a) Gib die Gleichung der Parabeln mit dem Scheitel S(1;2) an.<br> | + | 2. a) Gib die Gleichung der Parabeln mit dem Scheitel S(1;2) an.<br> |
b) Welche dieser Parabeln geht durch den Punkt P(2;0)? | b) Welche dieser Parabeln geht durch den Punkt P(2;0)? | ||
| Zeile 282: | Zeile 284: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
| − | a) <math>f(x) = ax^2 - 2a x + | + | a) <math>f(x) = ax^2 - 2a x + a + 2</math> |
| − | b) a = - | + | b) a = - 2 |
}} | }} | ||
</div> | </div> | ||
| Zeile 302: | Zeile 304: | ||
* [http://www.studienseminare-ge-gym.nrw.de/K/riemer/mathematik/publikationen/videoanalyse/index-videoanalyse.htm Videoanalyse: Geschwindigkeit und Bremswege] von [http://www.riemer-koeln.de/joomla/ Wolfgang Riemer] | * [http://www.studienseminare-ge-gym.nrw.de/K/riemer/mathematik/publikationen/videoanalyse/index-videoanalyse.htm Videoanalyse: Geschwindigkeit und Bremswege] von [http://www.riemer-koeln.de/joomla/ Wolfgang Riemer] | ||
| − | * [ | + | * [https://www.geogebra.org/m/T4RUNcxv Funktionsterm bestimmen - Die Waldschlösschenbrücke Dresden] von Heinz Lindner. |
---- | ---- | ||
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | ||
| − | [[ | + | [[Quadratische_Funktionen_2_Startseite|'''Startseite''']] - [[Quadratische_Funktionen_2_-_Bremsweg|'''1. Bremsweg''']] - [[Quadratische_Funktionen_2_-_Bremsbeschleunigung|'''2. Unterschiedliche Straßenverhältnisse''']] - [[Quadratische_Funktionen_2_-_Übungen1|'''3. Übungen 1''']] - [[Quadratische_Funktionen_2_-_Köln-Arena|'''4. Köln-Arena''']] - [[Quadratische_Funktionen_2_-_Einfluss_der_Parameter|'''5. Einfluss der Parameter in der Scheitelform''']] - [[Quadratische_Funktionen_2_-_Übungen2|'''6. Übungen 2''']] - [[Quadratische_Funktionen_2_-_Allgemeine_quadratische_Funktion|'''7. Allgemeine quadratische Funktion''']] - [[Quadratische_Funktionen_2_-_Übungen3|'''8. Übungen 3''']] - [[Quadratische_Funktionen_2_-_Aufgaben|'''9. Aufgaben''']] |
Aktuelle Version vom 9. Dezember 2020, 07:59 Uhr
Startseite - 1. Bremsweg - 2. Unterschiedliche Straßenverhältnisse - 3. Übungen 1 - 4. Köln-Arena - 5. Einfluss der Parameter in der Scheitelform -
6. Übungen 2 - 7. Allgemeine quadratische Funktion - 8. Übungen 3 - 9. Aufgaben
Hier lernst du, wenn du noch Lust hast, einiges über den Anhalteweg eines Autos, Springbrunnen, ... und du kannst noch üben.
Inhaltsverzeichnis |
Der Anhalteweg
Wir haben oben gesehen, dass man selbst bei relativ moderaten Geschwindigkeiten mit beachtlichen Bremswegen rechnen muss. Dabei blieb jedoch noch unberücksichtigt, dass der Anhalteweg nicht allein der reine Bremsweg ist, sondern dass zum Bremsweg auch noch der sogenannte Reaktionsweg hinzukommt.
Der Bremsweg ist derjenige Weg, den das Fahrzeug vom Beginn des Bremsvorgangs bis zum Stillstand zurücklegt. Er berücksichtigt also nicht, dass man nach dem Auftreten des Hindernisses eine gewisse Zeit (die Reaktionszeit') benötigt, bis man überhaupt reagieren kann und bremst. Der Weg, den das Fahrzeug angesichts der Reaktionszeit noch ungebremst zurücklegt, nennt man Reaktionsweg.
Aufgabe
|
Experimentieren mit einem Applet zum Anhalteweg
|
Im folgenden Applet ist der Zusammenhang zwischen Geschwindigkeit und Anhalteweg dargestellt worden. Mit Hilfe der Schieberegler können Geschwindigkeit v, Bremsbeschleunigung aB und Reaktionszeit tR variiert werden.
Löse mit diesem Applet indem du experimentierst und die Werte abliest folgende Aufgabe.
|
Den Einfluss der verschiedenen Faktoren auf die Länge des Anhalteweges kannst du auch mit diesem Applet untersuchen.
Beim Bremsen eines Pkws ist der also Zusammenhang zwischen der Geschwindigkeit und dem zurückgelegten Weg durch eine quadratische Funktion der Form
f(x) = ax2 + bx beschrieben, wobei der reinquadratische Teil den Bremsweg und der lineare Teil den Reaktionsweg bestimmt.
|
Übungen
Aufgabe 5: Anhalteweg Die Funktion s(v) = 0,1v2 + 1,5v ist ein Beispiel für eine Funktion, die den Zusammenhang zwischen der anfänglichen Geschwindigkeit eines Fahrzeuges in m/s und dem Anhalteweg für einen konkreten Bremsvorgang angibt.
|
Aufgabe 6: Bestimme a und b
|
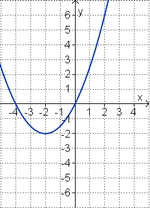
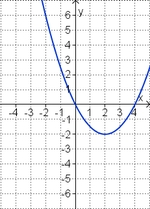
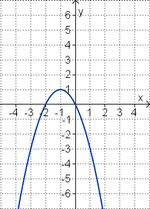
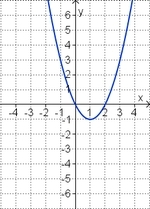
Aufgabe 7: Term und Graph zuordnen
Ordne den Funktionsgraphen den richtigen Term zu.
f(x) = 2x2 - 4x (!Die Parabel ist nach unten geöffnet.) (Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [-1|6] liegt auf dem Graphen.) (!Der Punkt [-1|-2] liegt auf dem Graphen.) f(x) = - 0,25x2 + 3x (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (!Die Parabel ist enger als die Normalparabel.) (Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|5] liegt auf dem Graphen.) (!Der Punkt [2|7] liegt auf dem Graphen.) Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der y-Achse symmetrisch zueinander sind? (!7x2 und -7x2) (7x2 - 2x und 7x2 + 2x) (!7x2 - 2x und -7x2 + 2x) (!7x2 - 2 und 7x2 + 2) (-7x2 + 2x und -7x2 - 2x) (!7x2 - 2 und 7x2 + 2x) |
Springbrunnen
|
Bei Wasserfontänen und Springbrunnen tritt der Wasserstrahl oftmals parabelförmig aus.
a) |
|
Weitere Aufgaben
|
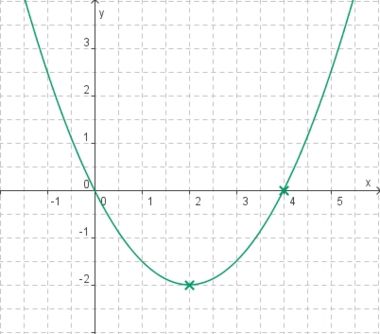
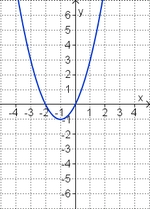
1. Bestimme die Gleichungen der abgebildeten Parabeln. Mache einen günstigen Ansatz für den Funktionsterm!
f: S(0;3) |
|
2. a) Gib die Gleichung der Parabeln mit dem Scheitel S(1;2) an. |
a) |
Weiterführende Links
Übungen im Internet:
- Übungen zum Erkennen quadratischer Funktionen
- Quadratische Ergänzung üben
- Zeichne den Graphen
- Graphen zeichnen
- Funktionsterm bestimmen - Die Waldschlösschenbrücke Dresden von Heinz Lindner.
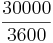 m in 1 Sekunde <=> 8,3 m in einer Sekunde
m in 1 Sekunde <=> 8,3 m in einer Sekunde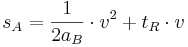
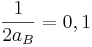 <=>
<=> 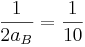 <=> 2aB = 10 <=> aB = 5 (m/s2)
<=> 2aB = 10 <=> aB = 5 (m/s2)

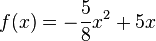
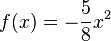
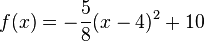

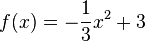
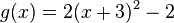 ;
; 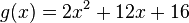
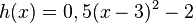 ;
; 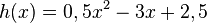
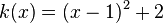 ;
;