Wurzelfunktion Einführung: Unterschied zwischen den Versionen
| (68 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | [[ | + | [[Wurzelfunktion_Startseite|Startseite]] --- [[Wurzelfunktion_Einführung|Die Wurzelfunktion]] - [[Wurzelfunktion_Übungen_1|Übungen]] - [[Wurzelfunktion_Anwendungen|Anwendungen]] - [[Wurzelfunktionen_Eigenschaften|Weitere Eigenschaften]] --- [[Wurzelfunktion_allgemeine_Wurzelfunktion|Die allgemeine Wurzelfunktion]] - [[Wurzelfunktion_Übungen_2|Übungen und Anwendungen]] --- [[Wurzelfunktion_Umkehrfunktion|Die Wurzelfunktion als Umkehrfunktion]] |
| + | __NOCACHE__ | ||
| + | ---- | ||
| + | {| width="99%" | ||
| + | | style="vertical-align:top" | | ||
| + | <!-- linke Spalte: Zwei div-Container --> | ||
| + | <div style="margin: 0; margin-right:10px; border: 2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#ffefd5; align:left;"> | ||
| + | Mit den nachfolgenden Übungen kannst du dein Vorwissen zum Rechnen mit Potenzen und Wurzeln aktivieren!<br> | ||
| + | [http://www.realmath.de/Neues/Klasse7/potenzen/potenzanwenden.html Potenzen anwenden]<br> | ||
| + | [http://www.mathe-online.at/tests/pot/potenzenWurzeln.html Potenz und Wurzeln]<br> | ||
| + | [http://www.mathe-online.at/tests/pot/rationaleExponenten.html Potenzen mit rationalen Exponenten] | ||
| − | + | </div> | |
| − | + | ||
| − | + | ||
| + | [[Bild:E Quadrat1.jpg|right|200px]] | ||
| + | Bei den folgenden Aufgaben bearbeitest du den Zusammenhang zwischen dem Flächeninhalt eines Quadrats und seiner Seitenlänge. <br>Ein Quadrat mit Seitenlänge <math>a</math> hat den Flächeninhalt <math> A = a^2</math>.<br><br> | ||
| + | Ist die Seitenlänge <math>a= 3 cm</math>, dann ist also der Flächeninhalt <math> A= 9 cm^2</math>. <br>Umgekehrt ist dann für ein Quadrat mit Flächeninhalt <math> A= 9 cm^2</math> die zugehörige Seitenlänge <math>a= 3 cm</math>.<br> | ||
| + | {{Arbeiten|NUMMER=1| ARBEIT= | ||
| + | Im folgenden Applet wird der Seitenlänge <math>a</math> eines Quadrats der Flächeninhalt <math>A</math> zugeordnet. <br>Der Punkt P hat die Koordinaten (<math>a| A</math>). Mit dem Schieberegler kannst du verschiedene Werte für <math>a</math> einstellen. | ||
| + | <center><ggb_applet width="444" height="532" version="4.0" ggbBase64="UEsDBBQACAAIADV3nkAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAA1d55AAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1ZW2/bNhR+7n7FgZ5aoIlJ3WwXdoumxbAA2Rog3TDsYQMl0TYbidRE2bGL/fgdkpIsxV2WW7dsQRyK5OG5fOfCY2X2ZlvksOGVFkrOPXpMPOAyVZmQy7m3rhdHE+/N629mS66WPKkYLFRVsHruhYZSZHOPs2ThB2F0NCHj6VEYpIujaUiyo4RMeZAEizSJAw9gq8UrqX5gBdclS/lFuuIFO1Mpq63gVV2Xr0ajq6ur41bUsaqWo+UyOd7qzANUU+q51zy8QnaDQ1eBJfcJoaOfvz9z7I+E1DWTKffAmLAWr795NrsSMlNXcCWyeoVmRL4HKy6WK7QpjtGmkSEqEZCSp7XYcI1He1Nrc12UniVj0uw/c0+Qd+Z4kImNyHg198hx4I/DIIj9SUAn0SSkHqhKcFk3tLSROWq5zTaCXzm25slKDD2olcoTZjjCH3+AT3wCL81A3eDjEMdui7g1ErjBd0PohsjRhO546EhDRxM6mhA9thFaJDmfewuWa0RQyEWF3uvmut7l3OrTLOytpy/RJi0+I3FAEFIHOa4T8tJ8YvyEpMG6ZyTtSa2r9R2FtiLDMLy9SP9BhgatTBpODmX60V+YGd8g1Nl9Gztp1IMWRdlf+zmQGNxk5nWJbv4wgXH4j5g4G7WpMmuyA/TK0DbRU/NCm3wJphBNTdhTiDA34jFGeQR0isPYB8wGoBGEEU7pBGIzjiEY40YIAUzA0NEAbHJEE/wTji2zGCJkZlbHmJNAUVAIUQDU5lQImElg8xJz1A+QIoogwkNGPPUNiyCGMMZZMIEQdTQpOaZIGOBBnKN4HwIKgTlMx+DHEBt+NDSpHk+M6sjSh5hATA1DzGrMaJfNSD+BwFgTN3AJWa7rAURpkbWPtSo7XyA11qN91XP1aVAUn81ylvAc74kL40mADctNRlhBCyVraJ3ou7VlxcqVSPUFr2s8peET27AzVvPtt0itW9mWNlVSn1eqfqfydSE1QKpy0umsctp79jutcRL0NsL+RtTbiHvP4y/KVbgDa81Rvqp0S86y7NRQ7EsDIvlB5ruTirPLUomhGbORvXJmfJ3mIhNM/oTBaqQYXKC7gUy5am+giIStIqrKLnYaIxi2v/BKIbTBMen/UDy3c1vhmBxP+z+oWspM7oXTwcYEd3bNVkSG/ILYieabzkNsyzvjl5VJ7MZwMznVJyrfL1nz37GyXle2d8DaWBmj3splzm2I2GqLF3N6majthYuNwPH6uCtxRpwCydLCDlga/ChCgmZM3GhpjGYdFbE0xFKQNthE1u3TqW8p7Ji40VJh9DrVGktpayYlrRihbUEj3iBtbOjPPebBWor6zM0whUR62ZhK3YEf1kXC9xFkCN4L15S4bmsohn5RzNvn7MWjSJqNrsXi7JJXkudN6KPT12qtXSb3siLjqShw6jYa7Jjx64+ok1vN+LLiDT3LbQPnkLW7pB/VB8uW1beVKk7l5iMGzTUFZqNWy5lOK1Ga2IQEr4tLvg+/TGiGt03WP2dyFdFIza2CgNQGLczidb1Sle3RsPjgaFI05wV2ZFDbOJTrglci7bnZdmUsXzd6d44zwINKPmFVvOYzO7E0uH0Qz5T4TbQCy8sVM20ibWKS7Xg1gMdy/F5lrfBGdG76SyiEtGwKtrU5xxKNNbPGBhvdIfcNtlOuqTnYlZn2HU9QGpin3dwb26WF2PZARZzEZ4wLNjBonzU11vNLbFq1Te26SWL78J3IMi47bZnECLJ+wJJWOnMBbxPugr47WqL5tnz0vN8458BNtuJ0gH/wDhzSNhY3eaRfO6x3On+QW/qjWbXIuZW9JBvw2gBNGpjt+LkXQtYKUw0HF6hbvZYpAyi2ZYXAG0Qb+07wm9sWoX3OXgJ54Q1BGv0Neif3Q8/0eUs3JG64L3x7pOhXR+pdDyl2V6TePT2k6FdD6n2LFLkHUu+fDlLkkZFKVVEwmYG0X2jOVb5bKuntW2xGTEECRm1aMt/GHAsMJs7edd2S4UWcY0tEHTX7jTr6xNHjJcSwj82cAo3YL+DuFGiB7Xjet1w/5r0W3tJp/s3VXvOlme0v5d/oYXwNVO11MLfV9dECbM/qHujz36U7ol2HJ4oyF6mou9jJzR15Kmvs97jtbg57tkvOS9NVf5AfKya1eW03vJxuj3TyNzjfPSRuC7N/Heajv7wc/gc4p08wno8OKub/AOjsCQF9PaD/Y4XjoGM47/dWvz73X9y1azi/V7V5hKaBfu32atg0fKjwayhe2iw/Q09f6x3OXTewfbsV+qBj4Dc3AyZwOrT4/UJ9+EblXyzcNLpzoD8M8t0XIV/cAfLFE4H8viX8gZCP+m9d7EvQ5v95r/8EUEsHCD8fGSPjBgAAbBwAAFBLAQIUABQACAAIADV3nkBFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgANXeeQD8fGSPjBgAAbBwAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAB7BwAAAAA=" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /></center> | ||
| + | a) Welcher Flächeninhalt <math>A</math> ergibt sich für <math>a</math> = 1; 1,5; 2 und 2,5? Halte deine Ergebnisse in Form einer Tabelle fest!<br> | ||
| + | b) Gib eine Funktionsgleichung an, die der Seitenlänge <math>a</math> den Flächeninhalt <math>A</math> eines Quadrats zuordnet!<br> | ||
| + | c) Welchen Wert nimmt <math>A</math> für <math>a</math> = 5; 10; 15 an? Verwende dazu deine Funktionsgleichung!<br> | ||
| + | d) Stelle mit dem Schieberegler für den Flächeninhalt <math>A</math> die Werte 1,44; 1,96; 2,25; und 7,29 ein. Lies die zugehörigen Seitenlängen <math>a</math> im Applet ab und ergänze deine Tabelle! | ||
| + | }} | ||
| − | |||
| − | |||
| − | + | ||
| + | Wie kannst du die Seitenlänge eines Quadrats bei gegebenem Flächeninhalt berechnen?<br> | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| − | + | <math> a = \sqrt A</math> <br>}} | |
| − | a | + | |
| − | + | ||
| − | |||
| − | |||
| − | {{Aufgabe|a) | + | {{Arbeiten|NUMMER=2| ARBEIT= |
| + | a) Setze in deine Formel verschiedene Werte für A ein und berechne a! Trage die Ergebnisse in eine Wertetabelle ein! | ||
| + | |||
| + | b) Stelle deine Wertepaare im Koordinatensystem (<math>A</math> entspricht der x-Achse, <math>a</math> entspricht der y-Achse) dar!}} | ||
| + | |||
| + | |||
| + | <br> | ||
| + | In der vorherigen Aufgabe hast du einigen Flächeninhalten exemplarisch ihre Seitenlänge zugeordnet. Mit dem folgenden Applet kannst du diesen Zusammenhang verallgemeinern. | ||
| + | |||
| + | <center> | ||
| + | <ggb_applet width="746" height="406" version="4.0" ggbBase64="UEsDBBQACAAIAJl2nkAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACACZdp5AAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1Z62/bNhD/3P0VB33agNgW9bQLu0ParliBri2Qbhj2jZJom4teE2nHLvrH7/iQLdlOmnjNkC2IQ5E88u5+95Qz/XFT5LBmjeBVOXPI0HWAlWmV8XIxc1ZyPhg7P774brpg1YIlDYV51RRUzpxAUfJs5rB4HETJOBjMkywbBCz0B4k7TwduOKbxZD4OXC9yADaCPy+r97RgoqYpu0qXrKDvqpRKzXgpZf18NLq5uRm2rIZVsxgtFslwIzIHUMxSzBz78Byv6x268TW557pk9Psv78z1A14KScuUOaBUWPEX3z2b3vAyq27ghmdyOXPiMHBgyfhiiTqFPk5GiqhGQGqWSr5mAo92plpnWdSOJqOl2n9mniDfqeNAxtc8Y83McYfE9yIvnEyCaBJMItfzHagazkppiYllOmqvm645uzH3qifNEiWTVZUnVF0JX76A53ouXKiBmMHDIYrMlmvWXN8MnhkCM4SGJjDHA0MaGJrA0AQo45oLnuRs5sxpLhBCXs4bNN9uLuQ2Z1oeu7BXn1ygToJ/RmLk54DBHAW/cC8CV3+Mzh0FSYejbFYPZNiyi4Pofuy8f6Sg3/Ijh+p5t6kX3cHQ6Hsf/UjY4Re6F/pXf444+nepeMjRzP8Zwyj4V1ScjtrwmNqIALFUtNZrJCuEihF/AuFEuTqBEOMhitGzQyATHGIPMAKAhBCEOCVjiNQYgx/jRgA+jEHRER90QIRj/BPE+rIIQrxMrcYYh0CQUQChD0THUQAYPaBjEePS85EiDCHEQ4o98dQVfgRBhDN/DAHKqMIwJkjo40GcI3sPfAK+Okxi8CKI1H0kUOEdjZXoeKUHkQsRURdiJGMUmwhG+jH4SpvIwsXLeiV7EKVF1j7Kqt7ZAqkxB+1TnclJvUz4bJrThOVYHK6UJQHWNFfRoBnNq1JCa0TPrC0aWi95Kq6YlHhKwJ90Td9RyTZvkFq0vDVtWpXiY1PJV1W+KkoBkFa5u5O5yknn2dtJjRO/sxF0N8LORtR5jk/yrXAHVoIh/6oRLTnNsreKYp8WEMkPZb592TB6XVe8r8Z0pOvMlK3SnGeclr+hsyouChfYlR2Vptqy48fjVpCqya62Aj0YNn+wpsI0RYLhpPsTO7A1Wz4Jh273B68UKVXBF0z6h8a4tbV7ods/ZY3H1jsT0Q3bab9oVGRbzdXkrXhZ5fslrf8rWstVozsGTIyN0uqyXORM+4hOtViO0+uk2lwZ5/DNXZ+2Nc5cI0Cy0LgD5gYvDJHAjokZNY2SbEflahpXU7itt/Fst08mnqbQY2JGTYXua0SzmpJWTeK2bLjQGc11enGjfX/mXDqwKrl8Z2YYQzy9tqoSc+D9qkjY3oUUwWtuWhHbY9WV4CqmLpGVJeuzJidZ0+8vf3g07tPRgdNOr1lTstzGCDrHqloJE/Kd8MlYygucmg2LMVX2/xXlNKsZWzSsVTHX7Z2xgN51u+5/tKyvetNUxdty/Qmd60CA6aiVcirShtfKhyHBunLN9m6acUGxLGXdcyqoUfVUlR8ESSoEMdxXclk1uoPDLIWjiuWcFdiugdT+Wq4K1vC04w66ZaP5ysrtDa3kyhhQJX9i+jyw497guH3k98T1rFcDzeslVU2kvTKnW9b04NE3/lJlfdBErrpPKHiprynoRrs30ERgdpXYf6M9yn3/baSz2Ql7GOUleCRW49YkDQfmfNPBFGHin9EtaE+ffXBJzPvX2NAKnQGkjXX98DPPMqZrvrUwOpA2A6a+WrfM6Mk1YyYOdkdr1F5nmY7xrW2OrKQT0w7vl86RPdoG5C6DdFOMNs655tDImZU9J+3vQsE8IBZnDfNnE6XmRUSpobJmr9Ka1YNI6WGxqRtEXkFqFXyF73UbxPb7AYEBiL8aiankAtwfnD5go68g+eo8JFVvuDBDYoZzoeyg5g0DEnjEDyPPj313Ej4yhq9PY2gfHork6yePJDlcJY8E7E97YM+G86cnBGcbzo8EYFoVBS0zKPWb1ccq3y6q0tn3+tTV8U6JdlnqaYCpr9Kg0X8lWzIs9Dm2ZsRQp4Y6M9Sq+cV2OjHsLdMTVjDsW5h3N55bDb5l1QzuaULv7mIi2ELNdoKkx77WE7TTHT1Sfe8527GTddLgwD+K7bMLNfurNEeEaTh5Uec85XLnVrmqz29Lie0n043Vcbt4zVitGv8P5aeGlkJ9n9gvjPc3Q/aEzODeFvLGCKT/QoavZP8bK7AnZIWvxMKJ7f+LFZKvWOFbv3F8mM8FkyYBaYx9//bMeipQjvOWNtGe73/CJketDLWtzAZmcNlKq3Q51cGY9d3Js+Ko/zXIY72hHL6gDLz72YmEDzbU3fjOLb5bxNd2ig9Cef6UUd4XEbctG+ckrHuCjjieBL3fXu6i5aDBzEzLOD9qKd98rV/sdu1vzkpbj9G0v6fvNfZ6/GzGb9ek34bi3KBIj1D8+BAUP/67KHZy/9gm8/gkyNbxZENTdrvXe4/7tjTqftGnv6C3/2B+8TdQSwcIzjTle1cHAAD9HgAAUEsBAhQAFAAIAAgAmXaeQEXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACACZdp5AzjTle1cHAAD9HgAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAO8HAAAAAA==" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | {{Arbeiten|NUMMER=3| ARBEIT= | ||
| + | a) Verändere mit dem Schieberegler den Wert von <math>A</math>! Wird jedem Wert <math>A</math> ein Wert <math>a</math> zugeordnet?<br> | ||
b) Welche Bedeutung haben die Koordinaten des Punktes P?<br> | b) Welche Bedeutung haben die Koordinaten des Punktes P?<br> | ||
c) Was stellt die Spur des Punktes P dar?}} | c) Was stellt die Spur des Punktes P dar?}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Merke| | {{Merke| | ||
| − | Die Funktion <math>f</math>, die jeder nicht negativen reellen Zahl x ihre Quadratwurzel <math> sqrt x</math> zuordnet heißt '''Quadratwurzelfunktion''' oder einfach nur ''' | + | Die Funktion <math>f</math>, die jeder nicht negativen reellen Zahl x ihre Quadratwurzel <math> \sqrt x</math> zuordnet heißt '''Quadratwurzelfunktion''' oder einfach nur '''Wurzelfunktion'''.<br> |
| − | <center><math> f: x \rightarrow \ sqrt x </math><br></center> | + | <center><math> f: x \rightarrow \sqrt x </math><br></center> |
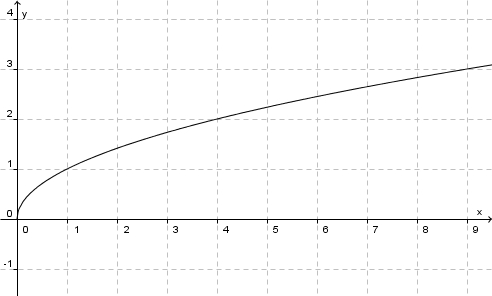
Ihr Graph schaut so aus:<br> | Ihr Graph schaut so aus:<br> | ||
<center>[[Bild:Graph_quadratwurzelfunktion.jpg]]</center> | <center>[[Bild:Graph_quadratwurzelfunktion.jpg]]</center> | ||
}} | }} | ||
| + | |||
| + | |||
| + | |||
| + | {{Arbeiten|NUMMER=4| ARBEIT= | ||
| + | Gib für die Quadratwurzelfunktion Definitions- und Wertemenge an.<br> | ||
| + | }} | ||
| + | |||
| + | |||
| + | Aufgabe 1 | ||
| + | {{Lösung versteckt|1= | ||
| + | a) 1; 2,25; 4; 6,25; 9<br> | ||
| + | b) A(a) = a<sup>2</sup><br> | ||
| + | c) 25; 100, 225<br> | ||
| + | d) 1,2; 1,4; 1,5; 2,7 | ||
| + | }} | ||
| + | |||
| + | Aufgabe 2 {{Lösung versteckt| | ||
| + | Dein Ergebnis kann so aussehen.<br> | ||
| + | a) [[Bild:Seitenlänge_in_Abhängigkeit_von_A.jpg]]<br> | ||
| + | b) [[Bild:Grafik_Seitenlänge_-_A.jpg ]] }} | ||
| + | |||
| + | Aufgabe 3 {{Lösung versteckt| | ||
| + | a) Ja! Jedem Wert <math> A </math> wird genau ein Wert <math>a</math> zugeordnet.<br> | ||
| + | b) Die x-Koordinate des Punktes P ist die Größe A des Flächeninhalts, die y-Koordinate die Länge a der Seite des Quadrats.<br> | ||
| + | c) Die Spur stellt den Graphen der Funktion a mit der Funktionsgleichung <math> a = sqrt A</math> dar. | ||
| + | }} | ||
| + | |||
| + | Aufgabe 4 {{Lösung versteckt|<math>D = R^+_0, W = R^+_0</math>}} | ||
| + | |||
| + | ---- | ||
| + | Die Wurzelfunktion hast du nun kennengelernt. Als nächstes kannst du zu [[Wurzelfunktionen_Übungen_1|Übungen]] oder [[Wurzelfunktion_Anwendungen|Anwendungen]] oder [[Wurzelfunktionen_Eigenschaften|Weitere Eigenschaften]] gehen. | ||
Aktuelle Version vom 27. April 2017, 07:16 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen - Weitere Eigenschaften --- Die allgemeine Wurzelfunktion - Übungen und Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
|
Bei den folgenden Aufgaben bearbeitest du den Zusammenhang zwischen dem Flächeninhalt eines Quadrats und seiner Seitenlänge.
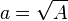
Aufgabe 1 a) 1; 2,25; 4; 6,25; 9 Aufgabe 2 Aufgabe 3 a) Ja! Jedem Wert Aufgabe 4 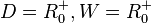 Die Wurzelfunktion hast du nun kennengelernt. Als nächstes kannst du zu Übungen oder Anwendungen oder Weitere Eigenschaften gehen. |
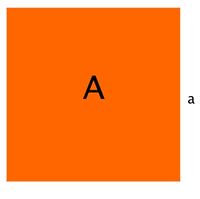
 hat den Flächeninhalt
hat den Flächeninhalt 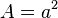 .
.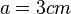 , dann ist also der Flächeninhalt
, dann ist also der Flächeninhalt 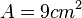 .
. 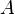 zugeordnet.
zugeordnet. 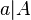 ). Mit dem Schieberegler kannst du verschiedene Werte für
). Mit dem Schieberegler kannst du verschiedene Werte für  , die jeder nicht negativen reellen Zahl x ihre Quadratwurzel
, die jeder nicht negativen reellen Zahl x ihre Quadratwurzel 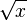 zuordnet heißt Quadratwurzelfunktion oder einfach nur Wurzelfunktion.
zuordnet heißt Quadratwurzelfunktion oder einfach nur Wurzelfunktion.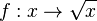
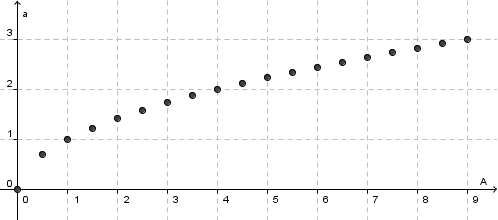
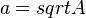 dar.
dar.

