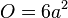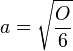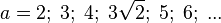Wurzelfunktion Anwendungen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Viele Anwendungen der Wurzelfunktion haben einen Faktor a. Daher wird als erstes die Funktion <math> f: x \rightarrow a \sqrt x </math> betrachtet. {{Arbeiten| N…“) |
|||
| (29 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | [[Wurzelfunktion_Startseite|Startseite]] --- [[Wurzelfunktion_Einführung|Die Wurzelfunktion]] - [[Wurzelfunktion_Übungen_1|Übungen]] - [[Wurzelfunktion_Anwendungen|Anwendungen]] - [[Wurzelfunktionen_Eigenschaften|Weitere Eigenschaften]] --- [[Wurzelfunktion_allgemeine_Wurzelfunktion|Die allgemeine Wurzelfunktion]] - [[Wurzelfunktion_Übungen_2|Übungen und Anwendungen]] --- [[Wurzelfunktion_Umkehrfunktion|Die Wurzelfunktion als Umkehrfunktion]] | |
| + | __NOCACHE__ | ||
| + | ---- | ||
| − | + | Viele Anwendungen der Wurzelfunktion haben einen Faktor a. Daher betrachten wir zuerst die Funktion <math> f: x \rightarrow a \sqrt x </math>. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
{{Arbeiten| | {{Arbeiten| | ||
| − | NUMMER= | + | NUMMER=12| ARBEIT= |
Gib die Funktion, die jeder Oberfläche eines Würfels die Kantenlänge zuordnet als Funktionsterm an. | Gib die Funktion, die jeder Oberfläche eines Würfels die Kantenlänge zuordnet als Funktionsterm an. | ||
# Bestimme zuerst einen Term für Oberfläche O eines Würfels in Abhängigkeit der Kantenlänge a. | # Bestimme zuerst einen Term für Oberfläche O eines Würfels in Abhängigkeit der Kantenlänge a. | ||
| − | # Löse den Term nach a auf. | + | # Löse den Term nach a auf und gib eine entsprechende Funktionsgleichung an. |
| − | # Bestimme a für O = 24; 54; 96; 150; 216; ... | + | # Bestimme a für O = 24; 54; 96; 108; 150; 216; ... und halte deine Ergebnisse in Form einer Tabelle fest! |
| − | # | + | # Zeichne den Graphen der Funktion! |
}} | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Arbeiten| | {{Arbeiten| | ||
| − | NUMMER= | + | NUMMER=13| ARBEIT= |
| − | Schau dir | + | Schau dir dieses Video an. Verwende zum Hören Kopfhörern! |
<center>{{#ev:youtube |iK9bhyl6B_E|350}}</center> | <center>{{#ev:youtube |iK9bhyl6B_E|350}}</center> | ||
| − | Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann | + | <div class="multiplechoice-quiz"> |
| + | |||
| + | Wie weit kannst du bis zum Horizont sehen? | ||
| + | Etwa (!50m) (!500m) (5km) (!50km) | ||
| + | </div> | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | |||
| + | MIt welcher Formel kannst du die Sichtweite a berechnen? | ||
| + | (<math>a = \sqrt{c^2-b^2} </math>) (!<math>a = \sqrt{b^2-c^2}</math>) (!<math>a = \sqrt{a^2-b^2}</math>) (!<math>a = \sqrt{c^2-a^2}</math>) | ||
| + | </div> | ||
| + | |||
| + | Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann bei guten Bedingungen näherungsweise durch die Formel <math> s = 3,57 \sqrt h</math> (vgl. [http://de.wikipedia.org/wiki/Sichtweite#Berechnung Sichtweite]) beschreiben werden. Dabei ist <math>h</math> die Augenhöhe in m und <math>s</math> die Sichtweite in km. | ||
| + | <br>Am besten gehst du von der Sichtweite auf dem Meer aus, da dort keine Berge stören. | ||
| + | <br>Ansonsten nimmt du die "ideale" Kugelgestalt der Erde ohne Berge und Täler. | ||
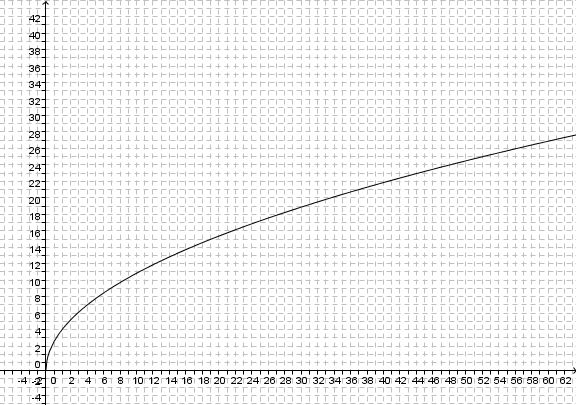
# Zeichne den Graphen zur Funktion <math> s: h \rightarrow 3,57 \sqrt h</math>. | # Zeichne den Graphen zur Funktion <math> s: h \rightarrow 3,57 \sqrt h</math>. | ||
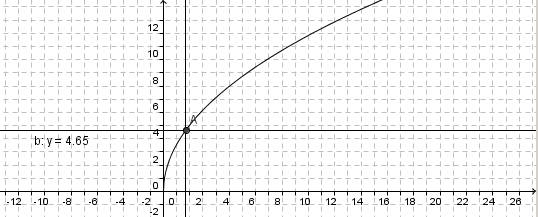
# Wie weit kann man bei einer Augenhöhe von 1,7m bei klarem Wetter sehen. Löse graphisch und rechnerisch. | # Wie weit kann man bei einer Augenhöhe von 1,7m bei klarem Wetter sehen. Löse graphisch und rechnerisch. | ||
| Zeile 50: | Zeile 43: | ||
}} | }} | ||
| − | {{Lösung versteckt| | + | |
| + | {{Arbeiten| | ||
| + | NUMMER=14| ARBEIT= | ||
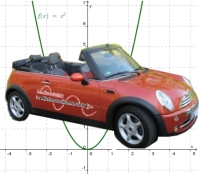
| + | [[datei:Parabelbrems.jpg|right]] | ||
| + | Bei den [http://wikis.zum.de/medienvielfalt/Quadratische_Funktionen_2 quadratischen Funktionen] hast du gelernt, dass der Bremsweg <math>s</math> eines Autos in m, welches mit der Geschwindigkeit <math>v</math> in km/h fährt, mit der Faustregel <math> s = (\frac {v}{10})^2</math> berechnet werden kann. | ||
| + | |||
| + | # Löse die Gleichung <math> s = (\frac {v}{10})^2</math> nach v auf. | ||
| + | # Gib die Funktion <math>f</math> mit Defintionsmenge an, die den Zusammenhang Bremsweg --> Geschwindigkeit beschreibt. | ||
| + | # Löse graphisch und rechnerisch: Mit welcher Geschwindigkeit <math>v</math> in km/h ist ein Auto, das eine Bremsspur von | ||
| + | a) 20m, <br> | ||
| + | b) 40m, <br> | ||
| + | c) 60m, <br> | ||
| + | d) 80m, <br> | ||
| + | e) 100m <br> | ||
| + | gemacht hat, gefahren?<br> | ||
| + | }} | ||
| + | |||
| + | |||
| + | Aufgabe 12 {{Lösung versteckt| | ||
| + | # <math> O = 6 a^2</math> | ||
| + | # <math> a = \sqrt{\frac{O}{6}} </math> | ||
| + | # <math> a = 2;\; 3;\; 4;\; 3\sqrt2;\; 5;\; 6;\; ...</math> | ||
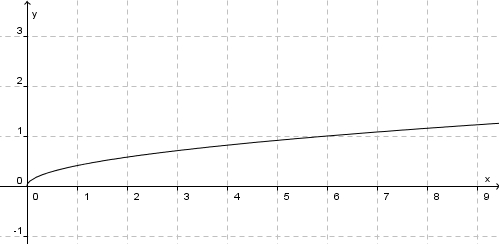
| + | # [[Datei:WurzelausO6.jpg]] | ||
| + | }} | ||
| + | |||
| + | Aufgabe 13 {{Lösung versteckt| | ||
# <br>[[Datei:Wurzelfunktion_3-57.jpg]] | # <br>[[Datei:Wurzelfunktion_3-57.jpg]] | ||
# 4,65km <br>[[Datei:Wurzelfunktion_3-57_2.jpg]] | # 4,65km <br>[[Datei:Wurzelfunktion_3-57_2.jpg]] | ||
| Zeile 56: | Zeile 74: | ||
# 786m | # 786m | ||
}} | }} | ||
| + | |||
| + | Aufgabe 14 {{Lösung versteckt| | ||
| + | # <math> v = 10 \sqrt s</math> | ||
| + | # <math> f: s \rightarrow 10 \sqrt s; D = R^+_0</math> | ||
| + | # Für die graphische Lösung kannst du in diesem Applet die entsprechenden Werte mit dem Schieberegler einstellen. | ||
| + | <ggb_applet width="806" height="594" version="4.0" ggbBase64="UEsDBBQACAAIALpaPEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIALpaPEAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1sxVjbbtw2EH1OvmKgp6SIvaIoStpgN0GTomgAJyngtCj6RkncXca6RaT2EuTjOyQlrdZ2HOfSFohNUhzO5cyZIZ3F831ZwFa0StbV0iPnvgeiyupcVuul1+nVWeI9f/ZwsRb1WqQth1XdllwvvdBIynzpJYmY8zTzz1YJz8/CPMQjWe6fMZGmcbBiQURREvZKPq3qN7wUquGZuMw2ouQXdca1NbzRunk6m+12u/PB1HndrmfrdXq+V7kH6Galll4/eYrqTg7tqBUPfJ/M/np94dSfyUppXmXCAxNCJ589fLDYySqvd7CTud6g9yT0YCPkeoMxxUHgwcwINQhIIzItt0Lh0cnSxqzLxrNivDL7D9wMijEcD3K5lblol55/ThLGfBqNvz2oWykq3cuS3uZs0LbYSrFzas3MWkQvdV0XKTca4dMnCPzAhydmIG4IcIgit+W7bz51Q+CG0A3MyYTueOhEQycTOpmQerCVSqaFWHorXihEUFarFrM3rpU+FML60384Rk+eYExKfkRh6mPyHeT43fefmJ8If0KzMTsNkkys6rb7SqODycSP7m8y+K5A6WCTMHLTZsA+E2Z0h1EX933iJGwCLZqy/+zPDYv0rjCvW3Tr7zMYhf9JiIvZUCqLvjpAbYxszx4tSmXqhc6BzQ3tCTCsjShGljMgcxziALAagDAIGS5JApEZY6AxboRAIQEjRyjY4mAJ/gpjqywChsrM1xhrEggaCoFRILamQsBKAluXWKMBRQnGgOEhY54ERgWNIIxwRRMI0UdTkjFBQYoHcY3mA6AEqDlMYggiiIw+EppSjxLjOqoMIPIhIkYhVjVWtKtmlE+AmmiiHi5ZNZ0+gSgr82Gq62bMBUpjPzp2PdefTprig0XBU1HgPXFpMgmw5YWpCGtoVVcahiQG7tu65c1GZupSaI2nFLznW37Btdj/itJqsG1ls7pSv7e1flkXXVkpgKwu/NHnuiCTeTB6jQs62QinG2yyEU3m8a12a9yBTgm0X7dqEOd5/spIHFsDIvm2Kg4vWsGvmlqehrGY2StnIbqskLnk1Z9IVmPF4ALjDWTa1XADsSgaHKnb/PKgkMGw/1u0NV4ByTmlbM7CmAYJo2SO5w5ui4XBOSWUkjhkoR+EMbqWcVN77DwIgzjEK8j355TROZ65fSuYO8tiOyaI78UY+7qV+XT+Sr2oi3xEwgb/kje6a+3LATtja0L6uVoXwhLE9lq8lrOrtN5fOmZQp+vdocGV7+ynaws6YGMIzF257sfUjVbGODZK+VbGtxL+QDWZj/tkHlgJO6ZutFLIXedaHygZoiT+YEYq285876RoLPHNJd9VUl8MCy2zqz5S4uTfdGUqjvQxAr9I9yJxT61TK+Tfs7KYXSPh4kq0lSh6zmO6u7pTroQn5ZCLTJa4dBs9bNyk9A/0yX3NxboVvTwv7MvNgWp3/Smdb3y2qn5t6/JVtX2HfLnmwGI2eLlQWSsbw0pI8Z64Ekfm5VJxvGby6TlTpIhGZq4TBEQbtLB8O72pW/s4w66Do6nNQpT4FANtKVh1pWhlNmKv7CsPnep6v0N/yJpBHur0PfbDawmzCyuD259hKfCi2XD7OOy5yA+iPcHGantd573lXk4V5lUJpaysmpLv7XsDFaYKe6XGhzVmozo+rJ1rfa9BSfNs35sL2s4OWKlzM1nJ/QRThEl+RFrwk3CO9aKxj1/hY1XZotZ9+drJbzLPRTX6yyskkE0DtjK8X7CQ8Q4Rju3jwQbDt21jkvo+MyZH+6ZFW0ZJD3GKf6TsUdselqAGPcY9d3OdJtV9H0/+yOT5dybv7WqlhDZoB5GFmt2VWVsiykiTPjM2Qx+X3tmRdd+SAvGhckeUaxuybAqZSf0lmAHT0eO8erR/jFDjA+cnUB9ajUvvJtCrrrIVN4K5+gLYk07z/WgfAfVvp56ptfuR71twvpuwvAfygCiuHqnHX8VZ/r9wNnEkDO7H2aGbkIGzEcXnBWOMBj6lUczmP47AiOStBJ5N2759fvX/k/DsH1BLBwgBRARt8gUAAOYQAABQSwECFAAUAAgACAC6WjxA1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIALpaPEABRARt8gUAAOYQAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAiQYAAAAA" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | <br> | ||
| + | a) 44,7 <math> \frac{km}{h}</math><br> | ||
| + | b) 63,2 <math> \frac{km}{h}</math><br> | ||
| + | c) 77,5 <math> \frac{km}{h}</math><br> | ||
| + | d) 89,4 <math> \frac{km}{h}</math><br> | ||
| + | e) 100 <math> \frac{km}{h}</math><br> | ||
| + | }} | ||
| + | ---- | ||
| + | |||
| + | Zurück zu [[Wurzelfunktion_Einführung|Wurzelfunktion]] oder weiter mit [[Wurzelfunktionen_Übungen_1|Übungen]] oder mit [[Wurzelfunktionen_Eigenschaften|Weitere Eigenschaften]]. | ||
Aktuelle Version vom 16. April 2017, 09:18 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen - Weitere Eigenschaften --- Die allgemeine Wurzelfunktion - Übungen und Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Viele Anwendungen der Wurzelfunktion haben einen Faktor a. Daher betrachten wir zuerst die Funktion 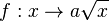 .
.
|
Gib die Funktion, die jeder Oberfläche eines Würfels die Kantenlänge zuordnet als Funktionsterm an.
|
|
Schau dir dieses Video an. Verwende zum Hören Kopfhörern! Wie weit kannst du bis zum Horizont sehen? Etwa (!50m) (!500m) (5km) (!50km) MIt welcher Formel kannst du die Sichtweite a berechnen?
( Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann bei guten Bedingungen näherungsweise durch die Formel
|
|
Bei den quadratischen Funktionen hast du gelernt, dass der Bremsweg
a) 20m, |
Aufgabe 12
Aufgabe 13
Aufgabe 14
-
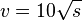
-
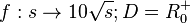
- Für die graphische Lösung kannst du in diesem Applet die entsprechenden Werte mit dem Schieberegler einstellen.
a) 44,7 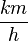
b) 63,2 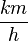
c) 77,5 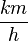
d) 89,4 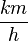
e) 100 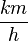
Zurück zu Wurzelfunktion oder weiter mit Übungen oder mit Weitere Eigenschaften.
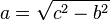 ) (!
) (!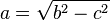 ) (!
) (!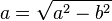 ) (!
) (!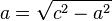 )
)
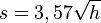 (vgl.
(vgl. 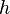 die Augenhöhe in m und
die Augenhöhe in m und  die Sichtweite in km.
die Sichtweite in km.
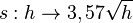 .
.
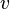 in km/h fährt, mit der Faustregel
in km/h fährt, mit der Faustregel 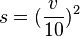 berechnet werden kann.
berechnet werden kann.
 mit Defintionsmenge an, die den Zusammenhang Bremsweg --> Geschwindigkeit beschreibt.
mit Defintionsmenge an, die den Zusammenhang Bremsweg --> Geschwindigkeit beschreibt.