Wurzelfunktion allgemeine Wurzelfunktion: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | [[ | + | [[Wurzelfunktion_Startseite|Startseite]] --- [[Wurzelfunktion_Einführung|Die Wurzelfunktion]] - [[Wurzelfunktion_Übungen_1|Übungen]] - [[Wurzelfunktion_Anwendungen|Anwendungen]] - [[Wurzelfunktionen_Eigenschaften|Weitere Eigenschaften]] --- [[Wurzelfunktion_allgemeine_Wurzelfunktion|Die allgemeine Wurzelfunktion]] - [[Wurzelfunktion_Übungen_2|Übungen und Anwendungen]] --- [[Wurzelfunktion_Umkehrfunktion|Die Wurzelfunktion als Umkehrfunktion]] |
| − | + | __NOCACHE__ | |
---- | ---- | ||
| Zeile 16: | Zeile 16: | ||
| − | {{Arbeiten|NUMMER= | + | {{Arbeiten|NUMMER=18| ARBEIT= |
Im folgenden Applet wird der Seitenlänge <math>a</math> eines Würfels das Volumen <math>V</math> zugeordnet. <br>Der Punkt P hat die Koordinaten (<math>a| V</math>). Mit dem Schieberegler kannst du verschiedene Werte für <math>a</math> einstellen. | Im folgenden Applet wird der Seitenlänge <math>a</math> eines Würfels das Volumen <math>V</math> zugeordnet. <br>Der Punkt P hat die Koordinaten (<math>a| V</math>). Mit dem Schieberegler kannst du verschiedene Werte für <math>a</math> einstellen. | ||
<br> | <br> | ||
| Zeile 27: | Zeile 27: | ||
d) Stelle mit dem Schieberegler für das Volumen <math>V</math> die Werte ein 1,728; 2,744; 3,375; 4,096; 4,913; 9,261; 15,625; 17,576. Lies die dazugehörigen Seitenlängen <math>a</math> im Applet ab und ergänze deine Tabelle! | d) Stelle mit dem Schieberegler für das Volumen <math>V</math> die Werte ein 1,728; 2,744; 3,375; 4,096; 4,913; 9,261; 15,625; 17,576. Lies die dazugehörigen Seitenlängen <math>a</math> im Applet ab und ergänze deine Tabelle! | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
}} | }} | ||
| Zeile 42: | Zeile 35: | ||
<math> a = V^{\frac{1}{3}}</math> | <math> a = V^{\frac{1}{3}}</math> | ||
| − | <math> a = \sqrt[3]{V} | + | <math> a = \sqrt[3]{V}</math><br> |
}} | }} | ||
| Zeile 48: | Zeile 41: | ||
{{Merke| | {{Merke| | ||
Die Gleichung <math> a = x^n</math> hat für jede natürliche Zahl n und jede nicht negative reelle Zahl a als Lösung<br> | Die Gleichung <math> a = x^n</math> hat für jede natürliche Zahl n und jede nicht negative reelle Zahl a als Lösung<br> | ||
| − | <center> <math> x = a^{\frac{1}{n}}</math> oder <math> x = \sqrt[n]{a} | + | <center> <math> x = a^{\frac{1}{n}}</math> oder <math> x = \sqrt[n]{a}</math></center> |
| − | <math> \sqrt[n]{a} | + | <math> \sqrt[n]{a}</math> heißt die''' n-te Wurzel aus a'''. |
}} | }} | ||
| − | {{Arbeiten|NUMMER= | + | {{Arbeiten|NUMMER=19| ARBEIT= |
a) Setze in deine Formel verschiedene Werte für das Würfelvolumen V ein und berechne welche Werte | a) Setze in deine Formel verschiedene Werte für das Würfelvolumen V ein und berechne welche Werte | ||
sich für die Seitenlänge a ergeben! Trage die Ergebnisse in eine Wertetabelle ein! | sich für die Seitenlänge a ergeben! Trage die Ergebnisse in eine Wertetabelle ein! | ||
<br>b) Stelle deine Wertepaare im Koordinatensystem dar (<math>V</math> entspricht der x-Achse, <math>a</math> entspricht der y-Achse)!}} | <br>b) Stelle deine Wertepaare im Koordinatensystem dar (<math>V</math> entspricht der x-Achse, <math>a</math> entspricht der y-Achse)!}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Zeile 72: | Zeile 57: | ||
Allgemein ist für jede natürliche Zahl <math>n</math> die allgemeine Wurzelfunktion <math>n</math>-ten Grades oder <math>n</math>-te Wurzelfunktion definiert mit | Allgemein ist für jede natürliche Zahl <math>n</math> die allgemeine Wurzelfunktion <math>n</math>-ten Grades oder <math>n</math>-te Wurzelfunktion definiert mit | ||
<br> | <br> | ||
| − | <math> f: x \rightarrow \sqrt[n]{x} | + | <math> f: x \rightarrow \sqrt[n]{x}</math> mit <math> x \in R^+_0</math> und <math>n \in N</math>. |
}} | }} | ||
| − | {{Arbeiten|NUMMER= | + | {{Arbeiten|NUMMER=20| |
| − | ARBEIT= Gib für die Würfelaufgabe die zugehörige | + | ARBEIT= Gib für die Würfelaufgabe die zugehörige Funktion mit Definitionsmenge an!}} |
| − | {{ | + | |
| − | <math>f: | + | {{Arbeiten|NUMMER=21| |
| + | ARBEIT= | ||
| + | # Zeichne für n = 1, 2, 3, 4, 5, 6 die Graphen der n-ten Wurzelfunktion <math> f: x \rightarrow \sqrt[n]{x}</math> | ||
| + | # Welche Punkte haben alle Graphen gemeinsam? | ||
}} | }} | ||
| − | {{ | + | Aufgabe 18: {{Lösung versteckt| |
| − | + | a) 1, 3,375; 8; 15,625<br> | |
| − | + | b) <math>V = a^3</math><br> | |
| − | + | c) 27; 125; 1000; 3375<br> | |
| + | c) 1,2; 1,4; 1,5; 1,6; 1,7; 2,1; 2,5; 2,6 | ||
}} | }} | ||
| − | {{Lösung versteckt| | + | Aufgabe 19: {{Lösung versteckt| |
| + | Dein Ergebnis kann so aussehen.<br> | ||
| + | a) [[Datei:Wuerfel_V-a-Tabelle.jpg]]<br> | ||
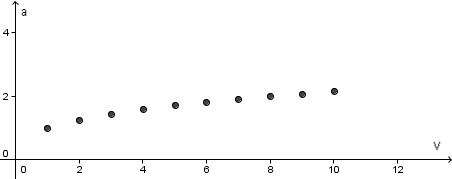
| + | b) [[Datei:Wuerfel_V-a-graph.jpg]]<br> | ||
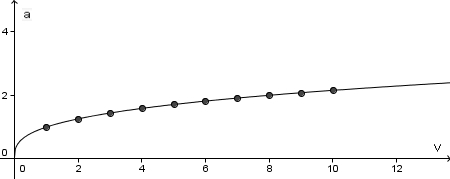
| + | Verbindet man die Punkte, dann erhält man diesen Graphen: | ||
| + | [[Datei:Wuerfel_V-a-graph_2.jpg]] }} | ||
| + | |||
| + | Aufgabe 20: {{Lösung versteckt| | ||
| + | <math>f:V \rightarrow \sqrt[3]{V}</math> mit <math>D = R^+_0</math>}} | ||
| + | |||
| + | Aufgabe 21: {{Lösung versteckt| | ||
1. Stelle mit dem Schieberegler die passende Wurzelfunktion ein. | 1. Stelle mit dem Schieberegler die passende Wurzelfunktion ein. | ||
| − | <ggb_applet width=" | + | <ggb_applet width="706" height="322" version="4.0" ggbBase64="UEsDBBQACAAIANw+pUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACADcPqVAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbL1XW2/bNhR+bn/FgZ42oLFJ6mYXdou1Q7EAaTcg3TDsYQAt0TYbiRREypeiP36HpGTLSRtk6DAjNkXx4/nOnczi9aGuYCdaI7VaRnRCIhCq0KVUm2XU2fXVLHr96vliI/RGrFoOa93W3C6jxCFliVvSPElyFl8l+by4SgqeXHGRl1drmjMeMy5mjEcAByNfKv2B18I0vBC3xVbU/EYX3HrirbXNy+l0v99PBqqJbjfTzWY1OZgyAlRTmWXUP7xEcReb9rGHM0Lo9M/3N0H8lVTGclWICJwJnXz1/NliL1Wp97CXpd0uo5wmEWyF3GydTSnaNHWgBh3SiMLKnTC4dTT1Ntu6iTyMK7f+LDxBdTInglLuZCnaZUQmbEYoZSRJZjSfs5xFoFsplO2xtOecDtIWOyn2Qax78oyopdW6WnEnEb58AUYYgRduoGFgOGRZWCLhHYnDwMKQhCENmCRsTwI0CZgkYJI4gp00clWJZbTmlUEPSrVuMXqnubHHSnh9+hdn6+kLtMnIzwiOCbo0uBzfE/LCfTP8JqT39chIOmK1bfcvSQfKnGRPp2TfZWg8cLKvmcnSb5iZPUIa7H6KnTQdcSKV//PfB4zxY2beZwzz7yPMkv/FxMV0KJVFXx1gtg7bZ48VtXH1Es8hnbu0p5BibWQ5ZnkKdI5DzgCrAWgKSYpTOoPMjTnEOS4kEMMMHI7G4IsjneFPknthGaQozL3NsSaBIlECaQzU11QCWEng6xJrlMWISFNIcZOjp8yJiDNIMpzFM0hQR1eSOUVgjBtxjvQMYgqx20xzYBlkTh5NXKlnM6c6imSQEcioE4hVjRUdqhnxM4idNVnvLqmazl64qKjL4dHq5hQLRGM/One90J8umuKzRcVXosJz4tZFEmDHK1cRnmitlYUhiCy827S82crC3AprcZeBT3zHb7gVh3eINgO3xxZamd9abd/qqquVASh0RU4664qOntlJa5zEo4VkvJCOFrLRc/5VXo0r0BmB/Lo1A5yX5bVDnFsDevJXVR3ftILfNVpemrGY+iNnIbqikqXk6g9MVsfi/AKnE8i1q+EEYvNkUES35e3RYAbD4S/Ratc2YnfmHsOMUTIh4w9KMQV39ZbMJ/PxZ4ab+qX03qY+NGJ3Cgo/iJO9m1aW4+dr80ZX5cl6b/Bb3tiu9bcF7IatM+MntamETwrfX/EoLu5W+nAbsiEOsj4eG5yRwL/aeEcDNgOWpgjox1UYPcYpdkIRjyEeQYb0kuVpnc6ZR/hxFUaPwnwNqvWG0sFKSgYaaXwLI9FFofhkX0aHCDol7U2YYdHI4q43lYYNH7p6Jc454wA/y3ANCferSxr6VZrjf0KzmN5LvcWdaJWo+kzHgHe6M6FwR0VQikLWOA0LveO4C+rvqFN4W4pNK3o8r/x9LbjVr5JxEj947UW9a3V9rXYfMWPuKbCYDlouTNHKxuUlrPB0uBPn3Cul4Xi4lON9rjTRG4U7RNAh1nkLi7azW936Kxn2GhxdRVaixgsYWJ+EqqtFK4uT85W/26FSXa93PETNOR706hM2wXsB8xOPweVvpCnwqtlydyOkfTLyo2gvXOOlvddlT9zjTOWuklDLcDbW/ODzFfjKYH+0eJnGWKjzZTpo1vcXvIm4tnFwdzHfP0IXiGAtDyOHoo/kZ8wJfmHMuVwstu47vJ8aX9O2r17/8IssS6FO2nKF2eNjgN2rCQnbCBFy/bSxQeN91xjFvQ+LD2Vdc1WC8heGd53yQY3OZxjH0+Dw9w8UpqB+RE/Q4GA8C67VWmKaHvtodHaArwNJL/pBFqwHkiGk6+jxkI8q5mHMaRo/iDp5YtTJI76PH/P92IPTcTX4s6j/t+rVP1BLBwg+GSn0dgUAAPMNAABQSwECFAAUAAgACADcPqVARczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIANw+pUA+GSn0dgUAAPMNAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAADgYAAAAA" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br> |
<br>2. (0;0 und (1;1) | <br>2. (0;0 und (1;1) | ||
}} | }} | ||
| − | |||
| − | |||
| − | |||
---- | ---- | ||
| − | Du hast nun die allgemeine Wurzelfunktion kennengelernt. | + | Du hast nun die allgemeine Wurzelfunktion kennengelernt. Es geht weiter mit [[Wurzelfunktion_Übungen_2|Übungen und Anwendungen]]. |
Aktuelle Version vom 16. April 2017, 09:31 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen - Weitere Eigenschaften --- Die allgemeine Wurzelfunktion - Übungen und Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Bei den folgenden Aufgaben bearbeitest du den Zusammenhang zwischen dem Volumen eines Würfels und seiner Seitenlänge.
Ein Würfel mit der Seitenlänge  hat das Volumen
hat das Volumen 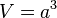 .
.
Ist die Seitenlänge 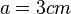 , dann ist also das Volumen
, dann ist also das Volumen 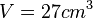 .
.
Umgekehrt ist dann für einen Würfel mit Volumen 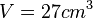 die zugehörige Seitenlänge
die zugehörige Seitenlänge 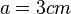 .
.
|
Im folgenden Applet wird der Seitenlänge
a) Welches Volumen |
Wie kannst du die Seitenlänge  bei gegebenem Volumen
bei gegebenem Volumen 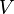 berechnen?
berechnen?
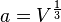
![a = \sqrt[3]{V}](/images/math/a/3/c/a3cad8c35c7c4e9e2f0ea5afff93ab52.png)
|
Die Gleichung 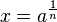 oder oder ![x = \sqrt[n]{a}](/images/math/4/6/9/469c5e753bca6920bc3a41f0f2cbf136.png)
|
|
a) Setze in deine Formel verschiedene Werte für das Würfelvolumen V ein und berechne welche Werte
sich für die Seitenlänge a ergeben! Trage die Ergebnisse in eine Wertetabelle ein!
|
|
Allgemein ist für jede natürliche Zahl |
|
Gib für die Würfelaufgabe die zugehörige Funktion mit Definitionsmenge an! |
|
Aufgabe 18:
a) 1, 3,375; 8; 15,625
b) 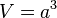
c) 27; 125; 1000; 3375
c) 1,2; 1,4; 1,5; 1,6; 1,7; 2,1; 2,5; 2,6
Aufgabe 19:
Aufgabe 20:
![f:V \rightarrow \sqrt[3]{V}](/images/math/5/6/2/56277ceb06d9f1e85ce77b321e54ee46.png) mit
mit 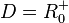
Aufgabe 21:
1. Stelle mit dem Schieberegler die passende Wurzelfunktion ein.
2. (0;0 und (1;1)
Du hast nun die allgemeine Wurzelfunktion kennengelernt. Es geht weiter mit Übungen und Anwendungen.

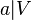 ). Mit dem Schieberegler kannst du verschiedene Werte für
). Mit dem Schieberegler kannst du verschiedene Werte für 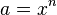 hat für jede natürliche Zahl n und jede nicht negative reelle Zahl a als Lösung
hat für jede natürliche Zahl n und jede nicht negative reelle Zahl a als Lösung![\sqrt[n]{a}](/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) heißt die n-te Wurzel aus a.
heißt die n-te Wurzel aus a.
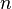 die allgemeine Wurzelfunktion
die allgemeine Wurzelfunktion ![f: x \rightarrow \sqrt[n]{x}](/images/math/1/4/c/14cf23945ed845ea63890d36ad846bcf.png) mit
mit  und
und 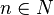 .
.