Wurzelfunktionen Eigenschaften: Unterschied zwischen den Versionen
| (18 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Wurzelfunktion_Startseite|Startseite]] --- [[Wurzelfunktion_Einführung|Die Wurzelfunktion]] - [[Wurzelfunktion_Übungen_1|Übungen]] - [[Wurzelfunktion_Anwendungen|Anwendungen]] - [[Wurzelfunktionen_Eigenschaften|Weitere Eigenschaften]] --- [[Wurzelfunktion_allgemeine_Wurzelfunktion|Die allgemeine Wurzelfunktion]] - [[Wurzelfunktion_Übungen_2|Übungen und Anwendungen]] --- [[Wurzelfunktion_Umkehrfunktion|Die Wurzelfunktion als Umkehrfunktion]] | [[Wurzelfunktion_Startseite|Startseite]] --- [[Wurzelfunktion_Einführung|Die Wurzelfunktion]] - [[Wurzelfunktion_Übungen_1|Übungen]] - [[Wurzelfunktion_Anwendungen|Anwendungen]] - [[Wurzelfunktionen_Eigenschaften|Weitere Eigenschaften]] --- [[Wurzelfunktion_allgemeine_Wurzelfunktion|Die allgemeine Wurzelfunktion]] - [[Wurzelfunktion_Übungen_2|Übungen und Anwendungen]] --- [[Wurzelfunktion_Umkehrfunktion|Die Wurzelfunktion als Umkehrfunktion]] | ||
| − | + | __NOCACHE__ | |
---- | ---- | ||
| − | Der Differenzenquotient <math>k = \frac{\bigtriangleup y}{\bigtriangleup x}</math> = <math>\frac{f(x_2)-f(x_1)}{x_2-x_1}</math> ist der Quotient der Änderung der Funktionswerte y durch die Änderung der Abszissenwerte x. | + | |
| − | <br> | + | |
| − | * Er gibt die '''Steigung einer Sekante''' durch die Punkte <math>\left( x_1 \mid f(x_1)\right)</math> und <math>\left( x_2\mid f(x_2)\right)</math> | + | Der Differenzenquotient <math>k = \frac{\bigtriangleup y}{\bigtriangleup x}</math> = <math>\frac{f(x_2)-f(x_1)}{x_2-x_1}</math> ist der Quotient der Änderung der Funktionswerte y durch die <br> |
| + | Änderung der Abszissenwerte x.<br> | ||
| + | |||
| + | * Er gibt die '''Steigung einer Sekante''' durch die Punkte <math>\left( x_1 \mid f(x_1)\right)</math> und <math>\left( x_2\mid f(x_2)\right)</math>. | ||
* Er ermöglicht die Berechnung des''' Steigungswinkels'''. | * Er ermöglicht die Berechnung des''' Steigungswinkels'''. | ||
* Er gibt die '''mittlere Änderungsrate''' an. | * Er gibt die '''mittlere Änderungsrate''' an. | ||
| − | + | ||
<br> | <br> | ||
{{Arbeiten| | {{Arbeiten| | ||
| − | NUMMER= | + | NUMMER=15| ARBEIT= |
Zeichne den Graphen der Funktionen <math>f(x) = 2 \cdot \sqrt{x}</math> und ermittle die Steigung der Sekante durch die Punkte <math>\left(0 \mid f(0)\right)</math> und <math>\left(2 \mid f(2)\right)</math>! | Zeichne den Graphen der Funktionen <math>f(x) = 2 \cdot \sqrt{x}</math> und ermittle die Steigung der Sekante durch die Punkte <math>\left(0 \mid f(0)\right)</math> und <math>\left(2 \mid f(2)\right)</math>! | ||
Gib den Steigungswinkel der Sekante an! | Gib den Steigungswinkel der Sekante an! | ||
| − | <br>Löse die | + | <br>Löse die Aufgabe mithilfe von GeoGebra oder einer Tabellenkalkulation!<br> |
}} | }} | ||
{{Arbeiten| | {{Arbeiten| | ||
| − | NUMMER= | + | NUMMER=16| ARBEIT= |
Gib für die folgenden zwei funktionalen Abhängigkeiten | Gib für die folgenden zwei funktionalen Abhängigkeiten | ||
| − | |||
| − | |||
| − | |||
a) Dem Oberflächeninhalt <math>A</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | a) Dem Oberflächeninhalt <math>A</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | ||
b) Dem Volumen <math>V</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | b) Dem Volumen <math>V</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | ||
| + | |||
| + | # die Funktionsgleichungen an und | ||
| + | # erstelle jeweils eine Wertetabelle und zeichne die Graphen der beiden Funktionen. | ||
| + | |||
}} | }} | ||
| + | |||
| + | |||
| + | {{Arbeiten| | ||
| + | NUMMER=17| ARBEIT= | ||
| + | |||
| + | Verwende die beiden funktionalen Abhängigkeiten aus Aufgabe 16 und | ||
| + | |||
| + | a) gib die mittlere Änderungsrate für beide Funktionen im Intervall [2;3] an! | ||
| + | |||
| + | b) halte schriftlich fest, welche Bedeutung die mittlere Änderungsrate in diesem Zusammenhang hat! | ||
| + | |||
| + | Löse die Aufgabe mithilfe von GeoGebra oder einer Tabellenkalkulation! | ||
| + | |||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | Aufgabe 15 {{Lösung versteckt| | ||
| + | [[Bild:Sekante_1.jpg|600px]] | ||
| + | |||
| + | <math> k = sqrt 2</math> | ||
| + | |||
| + | <math> tan(\alpha) = sqrt 2 \Rightarrow \alpha = 54,74^o</math> | ||
| + | }} | ||
| + | |||
| + | Aufgabe 16 {{Lösung versteckt| | ||
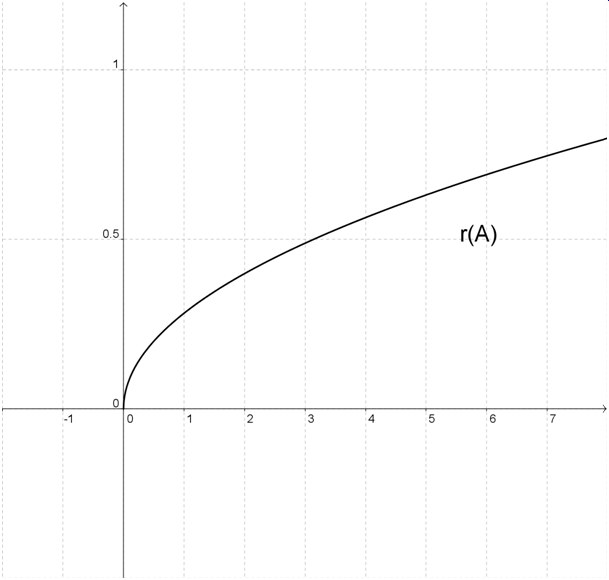
| + | 1. <math>r(A) = sqrt \frac{A}{4\pi}</math> | ||
| + | |||
| + | [[Bild:R(A).jpg]] | ||
| + | |||
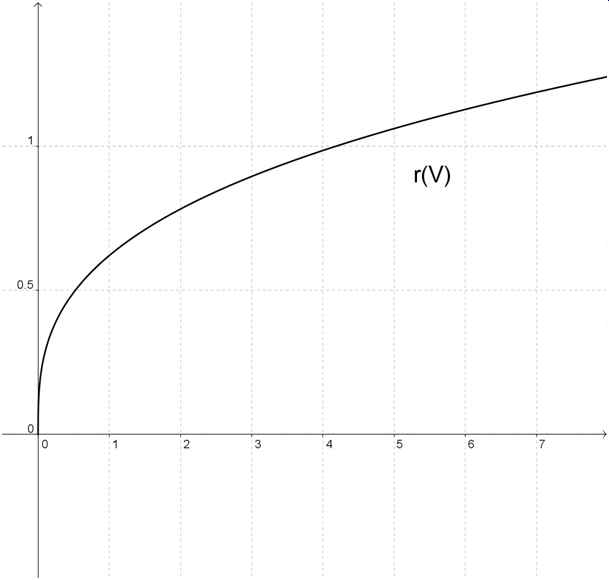
| + | 2. <math>r(V) = \sqrt[3]{\frac{3V}{4\pi}}</math> | ||
| + | |||
| + | [[Bild:R(V).jpg]] }} | ||
| + | |||
| + | Aufgabe 17 {{Lösung versteckt| | ||
| + | 1. a) <br> | ||
| + | [[Bild:Sekante_2.jpg]] | ||
| + | |||
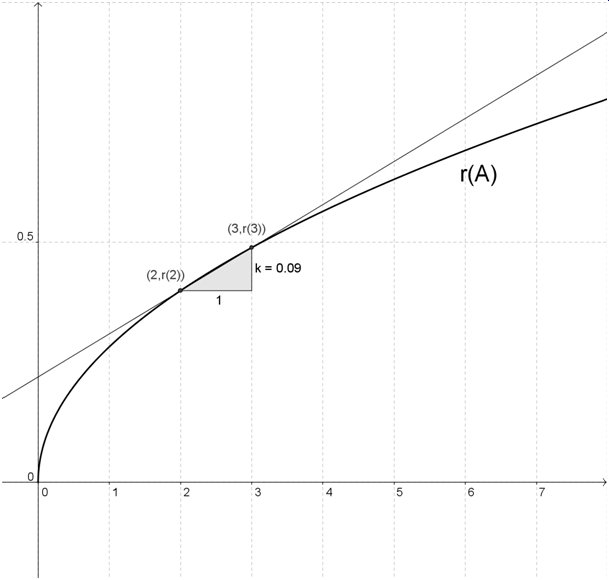
| + | b) Die mittlere Änderungsrate bedeutet in diesem Zusammenhang das Verhältnis der Änderung des Radius zur Änderung der Oberfläche einer Kugel im Intervall [2;3]. | ||
| + | |||
| + | 2. a)<br> | ||
| + | [[Bild:Sekante_3.jpg]] | ||
| + | |||
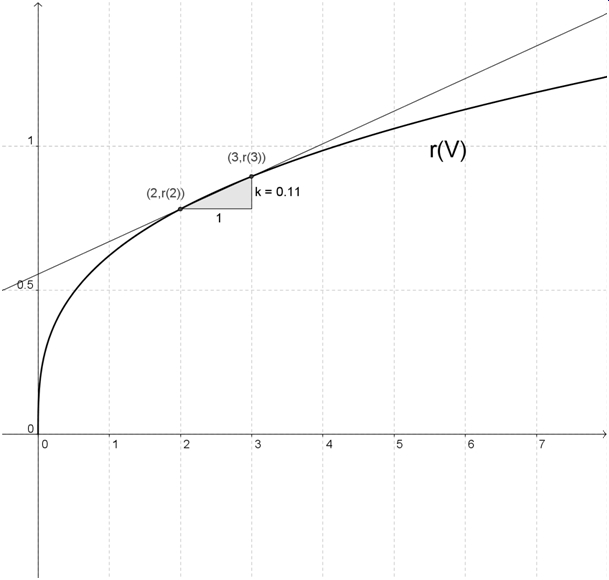
| + | b) Die mittlere Änderungsrate bedeutet in diesem Zusammenhang das Verhältnis der Änderung des Radius zur Änderung der Oberfläche einer Kugel im Intervall [2;3]. | ||
| + | }} | ||
| + | |||
| + | ---- | ||
| + | |||
| + | Zurück zu [[Wurzelfunktion_Einführung|Wurzelfunktion]] oder weiter mit [[Wurzelfunktionen_Übungen_1|Übungen]] oder mit [[Wurzelfunktion_Anwendungen|Anwendungen]]. | ||
Aktuelle Version vom 16. April 2017, 09:18 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen - Weitere Eigenschaften --- Die allgemeine Wurzelfunktion - Übungen und Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Der Differenzenquotient 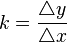 =
= 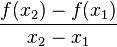 ist der Quotient der Änderung der Funktionswerte y durch die
ist der Quotient der Änderung der Funktionswerte y durch die
Änderung der Abszissenwerte x.
- Er gibt die Steigung einer Sekante durch die Punkte
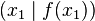 und
und 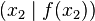 .
.
- Er ermöglicht die Berechnung des Steigungswinkels.
- Er gibt die mittlere Änderungsrate an.
|
Zeichne den Graphen der Funktionen Gib den Steigungswinkel der Sekante an!
|
|
Gib für die folgenden zwei funktionalen Abhängigkeiten a) Dem Oberflächeninhalt
|
|
Verwende die beiden funktionalen Abhängigkeiten aus Aufgabe 16 und a) gib die mittlere Änderungsrate für beide Funktionen im Intervall [2;3] an! b) halte schriftlich fest, welche Bedeutung die mittlere Änderungsrate in diesem Zusammenhang hat! Löse die Aufgabe mithilfe von GeoGebra oder einer Tabellenkalkulation! |
Aufgabe 15
Aufgabe 16
Aufgabe 17
b) Die mittlere Änderungsrate bedeutet in diesem Zusammenhang das Verhältnis der Änderung des Radius zur Änderung der Oberfläche einer Kugel im Intervall [2;3].
b) Die mittlere Änderungsrate bedeutet in diesem Zusammenhang das Verhältnis der Änderung des Radius zur Änderung der Oberfläche einer Kugel im Intervall [2;3].
Zurück zu Wurzelfunktion oder weiter mit Übungen oder mit Anwendungen.
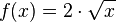 und ermittle die Steigung der Sekante durch die Punkte
und ermittle die Steigung der Sekante durch die Punkte 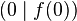 und
und 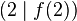 !
!
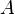 einer Kugel wird die Länge des Radius
einer Kugel wird die Länge des Radius  zugeordnet.
zugeordnet.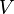 einer Kugel wird die Länge des Radius
einer Kugel wird die Länge des Radius 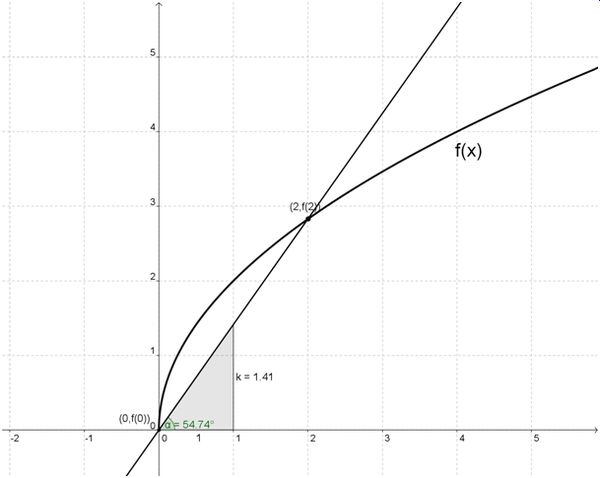
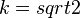
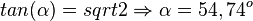
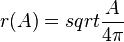
![r(V) = \sqrt[3]{\frac{3V}{4\pi}}](/images/math/d/b/1/db11e95046d35a65f24d9a28e636f23e.png)