Diskret - kontinuierlich: Unterschied zwischen den Versionen
(→Begriffsbildung) |
(→Ausblick) |
||
| Zeile 140: | Zeile 140: | ||
= Ausblick = | = Ausblick = | ||
| + | |||
| + | Oftmals ist bei realitätsnahen Modellen nicht möglich die gegebenen Differentialgleichung(en) exakt zu lösen. Aus diesem Grund ist es zielführend manchmal Näherungsverfahren zu verwenden. | ||
| + | |||
=== [[Näherungsverfahren]] === | === [[Näherungsverfahren]] === | ||
Version vom 23. August 2011, 11:33 Uhr
Diskret - kontinuierlich
erstellt von
Matthias Kittel und Walter Wegscheider
im Rahmen eines internationalen Projektes von
Medienvielfalt im Mathematikunterricht
(Stand August 2011)
Du erwirbst / stärkst in diesem Lernpfad folgende Kompetenzen
Das kennst du schon
- Darstellungsformen von Funktionen
- Kenntnis der Auswirkung von Variationen in verschiedenen Darstellungsformen (lineare, quadratische Funktionen, Potenzfunktionen, trigonometrische Funktionen u.a.)
Das lernst du
- Wie beschreibt man diskrete dynamische Vorgänge mit Hilfe von Differenzengleichungen - Lösungsmöglichkeiten und Visualisierung an verschiedenen Beispielen
- Wie beschreibt man kontinuierliche dynamische Vorgänge mit Hilfe von Differentialgleichungen - Visualisierung und Lösungsansätze mit Hilfe verschiedener Technologieunterstützungen an verschiedenen Beispiele
Du stärkst diese Kompetenzen:
- Darstellen, Modellieren (Heronverfahren, Radioaktiver Zerfall, Räuber-Beute-Modell, Rekursionsmodelle und Differenzengleichungen Differentialgleichung)
- Rechnen, Operieren (Radioaktiver Zerfall - analytische Herleitung sowie weiterführende Aufgaben, Herleitung der logistischen Gleichung, Lösen von Differentialgleichungen)
- Interpretieren (exponentielles Wachstum - Lebensmittelkontrolle, exponentielle Abnahme - radioaktiver Zerfall)
- Argumentieren, Begründen (Unterschied zwischen Differenzen- und Differentialgleichung)n
- Problemlösen (Erkennen der Einsatzgebiete von Differenzen- und Differentialgleichung)
Informationen zum Einsatz des Lernpfads im Unterricht: Didaktischer Kommentar
Der didaktische Kommentar als pdf.
Inhaltsverzeichnis |
Rekursive Beschreibung von Veränderungen
Unter rekursiven Verfahren kannst Du Dir Verfahren vorstellen, die errechnete Ergebnisse einer Formel wieder als Anfangswerte in die Formel einsetzen. Rekursion ist lateinisch und bedeutet zurücklaufen.
Rekursive Verfahren sind im Allgemeinen schrittweise (iterative) Verfahren. Das beudeutet, dass Du kein Ergebnis einfach ausrechnest, sonder Dich (langsam) an ein Ergebnis herantastest. Du näherst Dich Schritt für Schritt einem (richtigen) Ergebnis. Die Ergebnisse aus der Rekursionsformel sind die schrittweisen Zwischenergebnisse, die zum (korrekten) Endergebnis führen.
Da Differentialgleichungen schwierig zu lösen sind, ist es oft einfacher diese Art von Gleichungen in eine Differenzengleichung umzuwandeln und dann diese zu lösen. Differenzengleichungen sind rekursive Verfahren und können entsprechend gelöst werden.
Differenzengleichung
Begriffsbildung
Eine Differenzengleichung ist eine Möglichkeit, dynamische Systeme abzubilden. Dabei wird eine Folge von diskreten (einzeln betrachtbaren, abzählbaren) Ereignissen rekursiv definiert. Jedes Folgenglied ist daher eine Funktion der vorhergehenden Folgenglieder.
Form: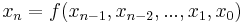 
für natürliche Zahlen 
.
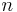Die Veränderung wird durch den Differenzenquotienten angegeben:
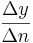mit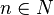 
Dabei entspricht:
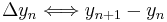und damit beispielsweise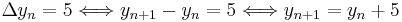 
Weiterführende Links:
- Differenzengleichungen, Josef Leydold, Differenzengleichungen, Abt. f. angewandte Statistik und Datenverarbeitung der WU Wien, 1997
- Systemdynamik, Peter Zierler, Systemdynamik - Querverbindung zwischen Mathematik und Informatik, NOEBIS
Software zur dynamischen Modellierung:
Themengebiete
Numerische Näherung - Heronverfahren
Radioaktiver Zerfall
Räuber-Beute-Modell
Cobweb/Spinnweben-Diagramm
Von der diskreten zur kontinuierlichen Veränderung
Wie Du Dir sicher vorstellen kannst, gibt es in der Realität kaum diskrete, das heißt abzählbare, Ereignisse. Die untersuchten Vorgänge laufen vielmehr kontinuierlich (stetig - ohne Sprünge) ab. Diese Kontinuität kannst Du erreichen, indem Du den Zeitschritt bei Differenzengleichungen immer kleiner machst oder die dem Problem zugeordnete Differentialgleichung analytisch (durch Ausrechnen löst). Zu diesem Thema sind hier fünf Gebiete für Dich aufgelistet, in denen auf Dich Aufgaben, Übungen und Beispiele warten.
Themengebiete
Unter folgenden vier Themengebieten kannst Du mehr über die Verwendung und den Einsatz von rekursiven Verfahren lernen und mittels Aufgaben, Beispielen und Erläuterungen Dein Wissen vertiefen.
Exponentielles Wachstum - Lebensmittelkontrolle
Radioaktiver Zerfall - analytische Herleitung und Beispiele
Abbau von Giftstoffen
Logistisches Wachstum - beschränktes Wachstum
Ein-Lebewesen-Modell nach Verhulst
Weitere Beispiele
- Bernd Huhn, Sonja Woltzen, Lehrer-Online, Fall mit Reibung - Ein Sprung aus 40.000m Höhe, 2005
- Josef Lechner, Freier Fall mit Luftwiderstand, ACDCA 1998
Differentialgleichungen
Begriffsbildung
Als (gewöhnliche) DGLG wird eine Gleichung bezeichnet, die neben einer Unbekannten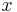 
auch deren Ableitung(en) 
(
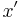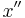, ...) enthält. Gelöst wird eine DGLG mittels Integralrechnung.
Die Lösung einer DGLG ist nicht wie bei einer herkömmlichen Gleichung eine Zahl, sondern eine Funktion, genauer eine Funktionenschar, die aus unendlich vielen Funktionen besteht. Da beim unbestimmten Integrieren immer eine Integrationskonstante auftritt, muss eine Zusatzinformation (Anfangsbedingung) gegeben sein, um die Konstante zu bestimmen.
Erst durch die Anfangsbedingung, die einem Punkt auf dem Graphen der Lösungsfunktion entspricht, kann die Lösungsfunktion exakt bestimmt werden. Die Lösung ist nun eine spezielle Funktion!
DGLG können in allen Bereichen des Lebens angetroffen werden, besonders in den Naturwissenschaften oder der Wirtschaft und dem Sport. In allen Zusammenhängen, bei denenen es um Veränderungen geht, kommen DGLG zur Anwendung.
Eine Übersicht über die Klassifikation von DGLG findet man unter Einteilung von Differentialgleichungen, T. Wolf, Fachhochschule Landshut (pdf-Datei, 14 kB)
Links:
- Differentialgleichungen, Josef Leydold, Abt. f. angewandte Statistik und Datenverarbeitung, 1997
- http://www.acdca.ac.at/material/kl8/diffequ.htm, Josef Böhm, Differentialgleichungen mit CAS, ACDCA 2004
Lösung einfacher Differentialgleichungen
Ausblick
Oftmals ist bei realitätsnahen Modellen nicht möglich die gegebenen Differentialgleichung(en) exakt zu lösen. Aus diesem Grund ist es zielführend manchmal Näherungsverfahren zu verwenden.
Näherungsverfahren
Beispiele:
- Exponentielles Wachstum - mit MAXIMA gelöst (wxm-Datei, 2 kB)
- Logistisches Wachstum - mit MAXIMA gelöst (wxm-Datei, 2 kB)
Links:
- Josef Lechner, Von Euler-Cauchy zu Runge-Kutta, ACDCA, 1998
- Urs Oswald, H.R. Schneebeli, Kugelstoßen mit Luftwiderstand, TI-Nachrichten 2/04 (pdf-Datei, 2,2 MB)
- H. Kohorst, Ph. Portscheller, P. Goldkuhle, Modellbildung und Simulation - NRW-Bildungsserver learn:line
© 2009, Projekt "Medienvielfalt im Mathematikunterricht"
