Quadratische Funktionen 2 Einfluss von a: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(Die Seite wurde neu angelegt: „{| | Wir betrachten nun den Einfluss von <math> \ a </math> in :<math> x \rightarrow a x^2 </math>. {{Arbeiten|NUMMER=A1|ARBEIT = <ggb_applet height="500" wid…“) |
|||
| Zeile 1: | Zeile 1: | ||
{| | {| | ||
| | | | ||
| − | Wir betrachten nun den Einfluss von <math> \ a </math> in | + | Wir betrachten nun den Einfluss von <math> \ a </math> in <math> x \rightarrow a x^2 </math>. |
| − | + | : | |
| + | |||
{{Arbeiten|NUMMER=A1|ARBEIT = | {{Arbeiten|NUMMER=A1|ARBEIT = | ||
| Zeile 8: | Zeile 9: | ||
filename="Qf-a.ggb" /> | filename="Qf-a.ggb" /> | ||
| − | # | + | # Mit dem Schieberegler kannst du den Wert von <math> \ a </math> ändern. <br> |
# Stelle den Schieberegler auf <math> \ a = 2 </math> ein. Wie ändert sich der Graph? <br> | # Stelle den Schieberegler auf <math> \ a = 2 </math> ein. Wie ändert sich der Graph? <br> | ||
# Überlege dir, wie sich die Werte <math> \ a = 3 </math> und <math> \ a = -1 </math> sowie <math> \ a = 0,5 </math> auf den Graphen auswirken und überprüfe deine Vermutung. <br> | # Überlege dir, wie sich die Werte <math> \ a = 3 </math> und <math> \ a = -1 </math> sowie <math> \ a = 0,5 </math> auf den Graphen auswirken und überprüfe deine Vermutung. <br> | ||
# Formuliere das Ergebnis deiner Untersuchungen.}} | # Formuliere das Ergebnis deiner Untersuchungen.}} | ||
| − | |||
|} | |} | ||
| Zeile 41: | Zeile 41: | ||
---- Verschiebung nach rechts | ---- Verschiebung nach rechts | ||
---- Verschiebung nach links | ---- Verschiebung nach links | ||
| − | ---- Streckung in <math> \ x </math>- Richtung | + | ---- Streckung in <math> \ x </math>- Richtung |
| − | ---- Stauchung in <math> \ x </math>- Richtung | + | ---- Stauchung in <math> \ x </math>- Richtung |
| − | +--+ Streckung in <math> \ y </math>- Richtung | + | +--+ Streckung in <math> \ y </math>- Richtung |
| − | -++- Stauchung in <math> \ y </math>- Richtung | + | -++- Stauchung in <math> \ y </math>- Richtung |
++-- Spiegelung an <math> \ x </math>- Achse | ++-- Spiegelung an <math> \ x </math>- Achse | ||
</quiz> | </quiz> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
---- | ---- | ||
<span style="background-color:yellow;">Hefteintrag:</span> Beachte, dass in der Lösung zur Aufgabe A1 ein Hefteintrag "versteckt" ist! | <span style="background-color:yellow;">Hefteintrag:</span> Beachte, dass in der Lösung zur Aufgabe A1 ein Hefteintrag "versteckt" ist! | ||
Version vom 13. Juli 2011, 16:18 Uhr
|
Wir betrachten nun den Einfluss von
|
|
|
Hefteintrag: Beachte, dass in der Lösung zur Aufgabe A1 ein Hefteintrag "versteckt" ist!
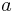 in
in 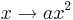 .
.
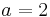 ein. Wie ändert sich der Graph?
ein. Wie ändert sich der Graph? 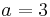 und
und 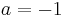 sowie
sowie 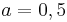 auf den Graphen auswirken und überprüfe deine Vermutung.
auf den Graphen auswirken und überprüfe deine Vermutung. 
