Quadratische Funktionen 2 - Übungen2: Unterschied zwischen den Versionen
| Zeile 62: | Zeile 62: | ||
| − | '''Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der y-Achse symmetrisch zueinander sind?''' (!7x<sup>2</sup> und -7x<sup>2</sup>) (7<math>[x - 2]^2 und 7[x + 2]^2</math>) (!x<sup>2</sup> - 2 und -7x<sup>2</sup> + 2) (!<math>7[x + 4]^2 - 2 und 7[x - 4]^2 + 2</math>) (-7<math>[x - 2]^2 + 2 und -7[x + 2]^2 + 2) | + | '''Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der y-Achse symmetrisch zueinander sind?''' (!7x<sup>2</sup> und -7x<sup>2</sup>) (7<math>[x - 2]^2</math> und <math>7[x + 2]^2</math>) (!x<sup>2</sup> - 2 und -7x<sup>2</sup> + 2) (!<math>7[x + 4]^2 - 2</math> und <math>7[x - 4]^2 + 2</math>) (-7<math>[x - 2]^2 + 2</math> und <math>-7[x + 2]^2 + 2</math>) |
Version vom 4. August 2011, 18:09 Uhr
Startseite - 1. Bremsweg - 2. Unterschiedliche Straßenverhältnisse - 3. Übungen 1 - 4. Köln-Arena - 5. Einfluss der Parameter in der Scheitelform -
6. Übungen 2 - 7. Allgemeine quadratische Funktion - 8. Übungen 3 - 9. Aufgaben
Übungen
Aufgabe 1: Funktionsterm finden
Aufgabe 2: Term und Graph zuordnen Ordne den Funktionsgraphen den richtigen Term zu.
Aufgabe 3: Multiple Choice Kreuze jeweils alle richtigen Aussagen an. f(x) = –
|
![-0,5[x - 1]^2 + 1](/images/math/4/c/7/4c73bf67f972faec8b107d99b3788f6d.png)
) (!![0,5[x + 2]^2 + 1](/images/math/d/6/f/d6ff352d488e3cbc0867b03e15bf2449.png)
) (!![-2[x - 2]^2 + 3](/images/math/2/b/2/2b2a8179711ecc6515f2229119565dbc.png)
) (![-0,5[x - 2]^2 + 1](/images/math/1/d/0/1d0b3a459d2226289a7d205eb44db292.png)
) (!![0,5[x - 1]^2 + 2](/images/math/8/a/3/8a36b2ef57a9deddaae6f151f4b0bf28.png)
)
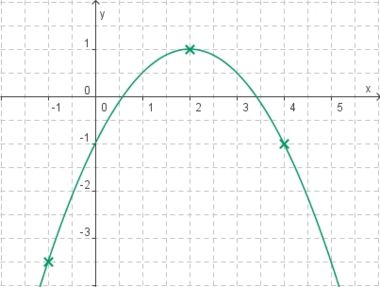
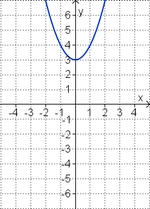
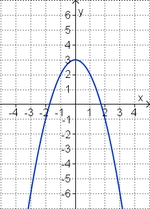
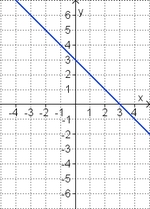
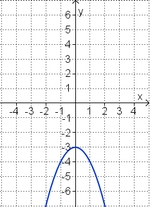
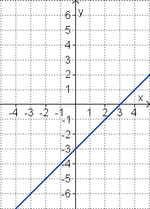
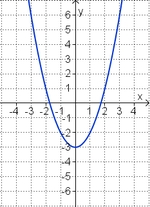
![2[x - \frac{3}{4}]^2](/images/math/f/b/c/fbc0dd591c46e8295c2e4c7e715edf01.png)
– 
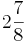(Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|-6] liegt auf dem Graphen.) (Der Punkt [1|1] liegt nicht auf dem Graphen.)
![7[x - 2]^2](/images/math/5/e/c/5ec8b8146ae36ed62a5f847e96dc0610.png)
) (!![7[x + 1]^2](/images/math/7/f/c/7fc8858eec2776e8217cef7bfdd8752d.png)
) (!![7[x - 4]^2 + 3](/images/math/e/2/a/e2a2c17d1fbc41912a957c18296f1d1f.png)
)
![[x - 2]^2](/images/math/a/4/4/a44def1464733c739700f0faeaeb914a.png)
und ![7[x + 2]^2](/images/math/8/8/e/88e76c7b0f4d8b134ea751e334d26a61.png)
) (!x2 - 2 und -7x2 + 2) (!![7[x + 4]^2 - 2](/images/math/5/b/9/5b909c506b5313322ee96324a56db7b8.png)
und ![7[x - 4]^2 + 2](/images/math/3/0/d/30d0733d96090c94c46cf16348b23e41.png)
) (-7![[x - 2]^2 + 2](/images/math/a/5/0/a500005940735e46bec601955b5d6e07.png)
und ![-7[x + 2]^2 + 2](/images/math/4/0/7/407bf0b9d1a3dee18e2f73026dc35355.png)
)
![7[x - 2]^2 - 2](/images/math/7/8/d/78d855dd49735b79ee45735f56dccd4d.png)
und ![7[x - 2]^2 + 2](/images/math/d/e/d/dedd18cce12567891e46fc55e73322b5.png)
) (!7x2 - 2 und 7x2 + 2) (7x2 - 2 und -7x2 + 2) (!7x2 - 2 und -7
|
Als nächstes beschäftigst du dich mit der allgemeinen quadratischen Funktion. |
