Beispiele: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Die folgenden Beispiele dienen zur Wiederholung, Anwendung und Vertiefung des bisher Gelernten. {{Arbeiten| NUMMER=1| ARBEIT= '''Geschwindigkeitsmessung''' …“) |
|||
| Zeile 9: | Zeile 9: | ||
<math>v = \frac {100}{t}</math> in <math> \frac{m}{s}</math>. | <math>v = \frac {100}{t}</math> in <math> \frac{m}{s}</math>. | ||
| − | Benutze ein Tool deiner Wahl, um die Zuordnung <math>t \right v(t)</math> grafisch darzustellen!<br> | + | a) Benutze ein Tool deiner Wahl, um die Zuordnung <math>t \right v(t)</math> grafisch darzustellen!<br> |
| − | Erstelle eine Wertetabelle!<br> | + | b) Erstelle eine Wertetabelle!<br> |
| − | Definiere <math>v</math> als Funktion <math>v: A \right B</math>! Begründe deine Wahl der Definitionsmenge A und der Zielmenge B!<br> | + | c) Definiere <math>v</math> als Funktion <math>v: A \right B</math>! Begründe deine Wahl der Definitionsmenge A und der Zielmenge B!<br> |
| − | Beschreibe in eigenen Worten, wie sich <math>v</math> für kleine und große t verhält! Wie zeigt sich dieses Verhalten an der Lage und Form des Graphen? | + | d) Beschreibe in eigenen Worten, wie sich <math>v</math> für kleine und große t verhält! Wie zeigt sich dieses Verhalten an der Lage und Form des Graphen? |
}} | }} | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| − | + | a) [[datei:Geschwindigkeitsmessung_graph.jpg ]]<br> | |
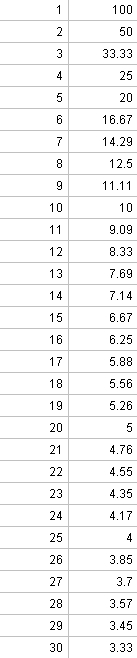
| + | b) [[datei:Geschwindigkeitsmessung_tabelle.jpg]]<br> | ||
| + | c) <math> A = R^+</math> ; <math> B = R^+</math><br> | ||
| + | d) kleine t: Geschwindigkeit geht gegen <math>\infty</math> ; große t: Geschwindigkeit geht gegen Null | ||
| + | }} | ||
{{Arbeiten| | {{Arbeiten| | ||
NUMMER=2| | NUMMER=2| | ||
ARBEIT= | ARBEIT= | ||
| + | |||
| + | }} | ||
'''Rechtwinkeliges Dreieck''' | '''Rechtwinkeliges Dreieck''' | ||
Version vom 27. Dezember 2011, 15:25 Uhr
Die folgenden Beispiele dienen zur Wiederholung, Anwendung und Vertiefung des bisher Gelernten.
|
Geschwindigkeitsmessung An einer Straße wird die Zeit, die vorbeifahrende Autos benötigen, um eine gekennzeichnete Strecke von 100 Metern zu durchfahren, gemessen. Wird die Zeitspanne t (in Sekunden) gemessen, so ergibt sich daraus eine Geschwindigkeit von
a) Benutze ein Tool deiner Wahl, um die Zuordnung Fehler beim Parsen(Syntaxfehler): t \right v(t) grafisch darzustellen! b) Erstelle eine Wertetabelle! |
Rechtwinkeliges Dreieck
Von einem rechtwinkeligen Dreieck mit Hypotenuse 1 ist eine Kathete a gegeben.
Drücke die andere Kathete 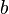 durch
durch  aus!
aus!
Benutze ein Tool deiner Wahl, um die Zuordnung Fehler beim Parsen(Syntaxfehler): a \right b(a)
grafisch darzustellen!
Erstelle eine Wertemenge mit Schrittweite 0,1!
Formuliere die Zuordnung als Funktion Fehler beim Parsen(Syntaxfehler): b: A \right B
! Begründe deine Wahl der Definitionsmenge A und der Zielmenge B!
Wie verhält sich der Funktionswert, wenn a nahe bei 1 liegt? Wie zeigt sich dieses Verhalten an der Lage und Form des Graphen?
}}
{{Arbeiten| NUMMER=3| ARBEIT=
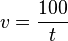 in
in 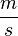 .
.
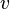 als Funktion Fehler beim Parsen(Syntaxfehler): v: A \right B
! Begründe deine Wahl der Definitionsmenge A und der Zielmenge B!
als Funktion Fehler beim Parsen(Syntaxfehler): v: A \right B
! Begründe deine Wahl der Definitionsmenge A und der Zielmenge B!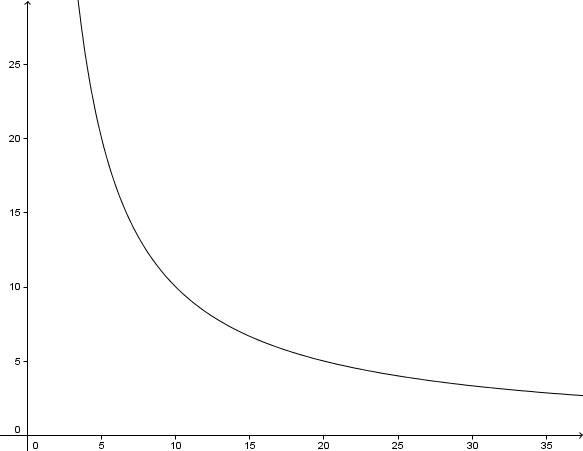
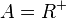 ;
; 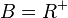
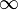 ; große t: Geschwindigkeit geht gegen Null
; große t: Geschwindigkeit geht gegen Null

