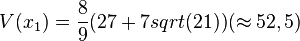Beispiele
Zuordnungen und Wertetabelle - Der Funktionsbegriff - Der Funktionsgraph - Beispiele und Übungen
Beispiele und Übungen
Die folgenden Beispiele dienen zur Wiederholung, Anwendung und Vertiefung des bisher Gelernten. Insbesondere sieht man wieder den engen Zusammenhang Funktionsterm, Funktionsgraph und Wertetabelle.
|
Wähle in diesem Arbeitsblatt die Funktionsdarstellungen (eindeutige Zuordnungen) aus. |
|
Geschwindigkeitsmessung An einer Straße wird die Zeit, die vorbeifahrende Autos benötigen, um eine gekennzeichnete Strecke von 100 Metern zu durchfahren, gemessen. Wird die Zeitspanne t (in Sekunden) gemessen, so ergibt sich daraus eine Geschwindigkeit von
a) Erstelle eine Wertetabelle! |
|
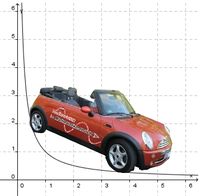
Bremsweg Für eine bestimmte PKW-Marke lässt sich der Bremsweg B (in Metern) bei einer Geschwindigkeit v (in km/h) in einer bestimmten Bremssituation durch folgenden Term darstellen: 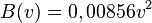 a) Formuliere diese Abhängigkeit als Funktion (d.h. wähle Definitions- und Zielmenge)! |
|
Temperaturkurve Öffne dieses Applet Temperaturkurve. Dort kannst du einen zeitlichen Temperaturverlauf bestimmen und mitverfolgen, wie die grafische Darstellung zustande kommt. |
|
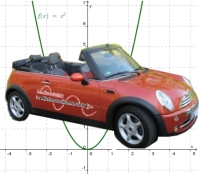
Funktionale Abhängigkeiten verstehen Rufe das Applet Funktionale Abhängigkeiten verstehen auf! Es zeigt eine weitere Darstellungsmöglichkeit für funktionale Abhängigkeiten. Mache dich mit der Funktionsweise dieses Werkzeugs vertraut! a) Studiere mit seiner Hilfe die Funktion 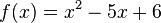 Für welche Werte von x ist f(x) = 0? (Damit hast du die Gleichung b) Mit diesem Tool kannst du auch das Schachtelbeispiel (Aufgabe 3) ein letztes Mal behandeln. Beantworte mit seiner Hilfe die Frage, für welches x das Volumen der Schachtel maximal ist! |
|
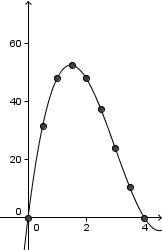
Erweitertes Schachtelbeispiel Zum Abschluss eine Verallgemeinerung des Schachtelbeispiels, in dem nicht von einem quadratischen, sondern von einem rechteckigen Stück Papier ausgegangen wird. Aus einem rechteckigen Stück Papier (Seitenlängen 8 und 10) soll eine Schachtel hergestellt werden. Dazu werden bei den Ecken vier kleinere (gleich große) Quadrate herausgeschnitten und das verbleibende Stück Pappe zu einer Schachtel (ohne Deckel) aufgeklappt. a) Ermittle eine Formel für das Volumen der Schachtel, wenn die Seitenlänge der herausgeschnittenen Quadrate mit x bezeichnet wird! |
Lösungen:
Aufgabe 13:
a) 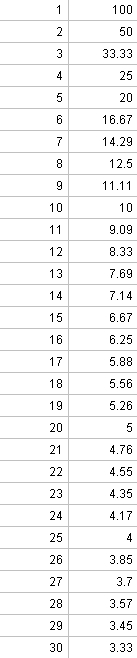
b) 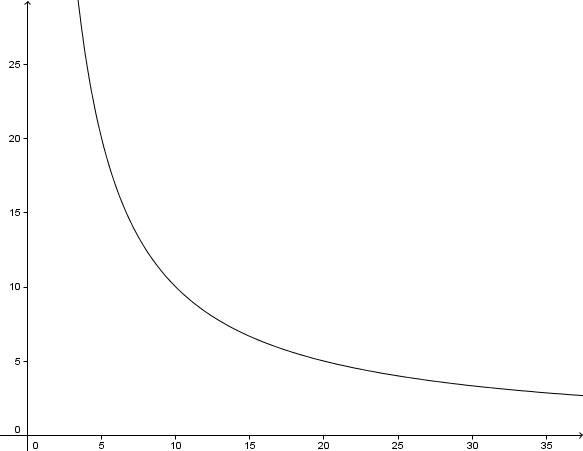
c) 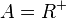 ;
; 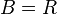 ; Wertemenge
; Wertemenge 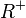
d) kleine t: Geschwindigkeit geht gegen 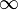 ; große t: Geschwindigkeit geht gegen Null
; große t: Geschwindigkeit geht gegen Null
Aufgabe 14:
a) 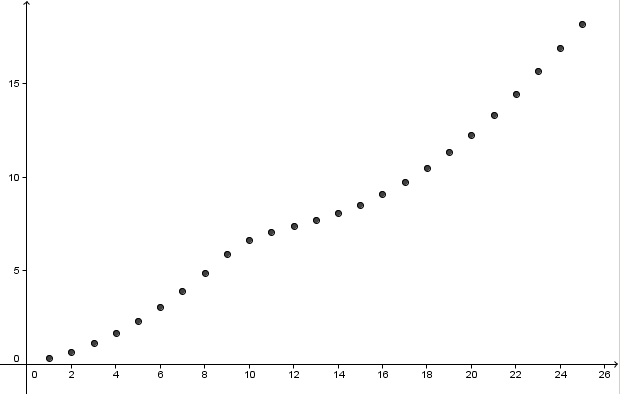
Der Zug fährt am langsamsten, wenn die Kurve am flachsten (am wenigsten steil) ist, also von der 11. bis zur 16. Minute.
b) Am Graph ist es einfacher zu erkennen,wann der Graph flacher ist, als in der Tabelle, wenn die Abstände kleiner sind.
Aufgabe 15:
a) Definitionsmenge: ![[0;300]](/images/math/4/1/6/4162558c1781e3a6f994c0f5b770b4d7.png) ; Zielmenge:
; Zielmenge: ![[0;300]](/images/math/4/1/6/4162558c1781e3a6f994c0f5b770b4d7.png)
Schneller als mit 300 km/h kommt man auf einer Autobahn sicher nicht voran!
b) 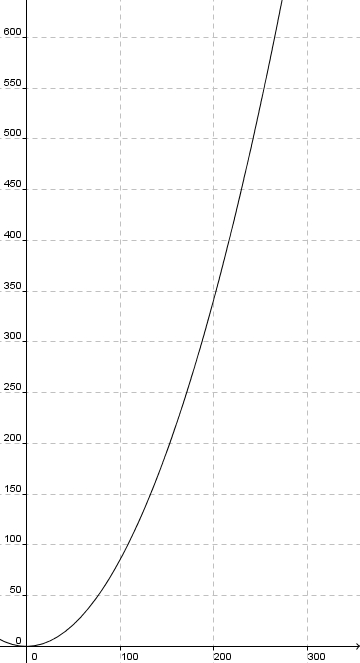
c) Bei niedrigen Geschwindigkeiten ist der Bremseweg klein, er wächst dann quadratisch mit der Geschwindigkeit, d.h. er nimmt mit wachsender Geschwindigkeit sehr viel schneller zu als die Geschwindigkeit selbst.
d) Bei Tempo 30 km/h beträgt der Bremsweg 7,704m.
e) B(25)=5,35; B(72)=44,38; B(104)=92,58; B(134)=153,7
Aufgabe 16:
Aufgabe 17:
a) f(x) = 0 für x = 2 oder x = 3
Aufgabe 18:
a) 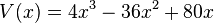 mit
mit 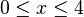
b) ![]()
c)
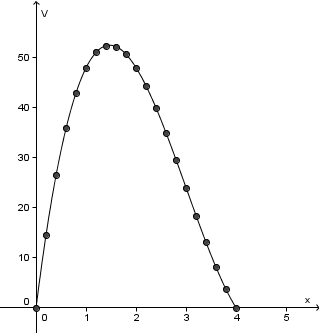
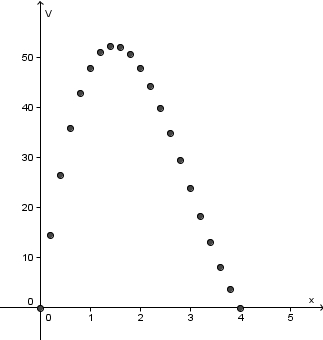 -
- 
d) Definitionsmenge: [0;4], Zielmenge 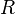 , Wertemenge [0;52,51]
, Wertemenge [0;52,51]
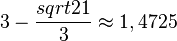 mit CAS berechnet!)
mit CAS berechnet!)Du hast nun das Ende des Lernpfads erreicht. Du kennst eine exakte Definition der Funktion und kannst sicher mit Funktionen und ihren Darstellungsformen umgehen. Du hast außerdem Funktionen als Objekte in der Mathematik kennengelernt. Als Objekte in der Mathematik haben Funktionen auch Eigenschaften. Du wirst bei der Behandlung weiterer Funktionstypen Eigenschaften von Funktionen wie Monotonie, Symmetrie, Einfluss von Parametern, ... erfahren. In der SII behandelst du dann Funktionen als Objekte der Mathematik und kannst dein ganzes bis dahin erworbenes Wissen anwenden.
 zurück zur Startseite
zurück zur Startseite
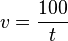 in
in 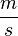 .
.
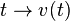 grafisch dar.
grafisch dar.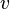 als Funktion
als Funktion 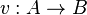 ! Begründe deine Wahl der Definitionsmenge A und der Zielmenge B!
! Begründe deine Wahl der Definitionsmenge A und der Zielmenge B!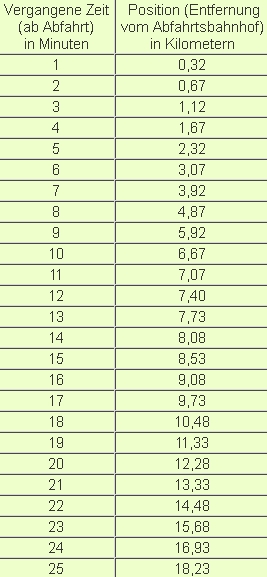
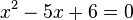 gelöst!)
gelöst!)
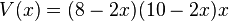
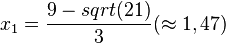 mit
mit