|
|
| Zeile 1: |
Zeile 1: |
| | Du hast nun Funktionen als Objekte in der Mathematik kennengelernt. Wir wollen als Nächstes untersuchen, welche Eigenschaften Funktionen haben. | | Du hast nun Funktionen als Objekte in der Mathematik kennengelernt. Wir wollen als Nächstes untersuchen, welche Eigenschaften Funktionen haben. |
| | | | |
| − | =Monotonie=
| + | Als Eigenschaften wollen wir Monotonie, Grenzwert und Symmetrie betrachten. |
| | | | |
| − | {{Arbeiten|NUMMER=1|
| + | [[Funktionen_Einstieg/Monotonie]] |
| − | ARBEIT=
| + | |
| − | Betrachte die folgenden Funktionen im angegebenen Intervall. Die Funktionen sind durch Funktionsterm und Graph gegeben. <br>
| + | |
| | | | |
| − | a) <math>f:x \rightarrow x^2</math> in <math>R^+</math> <center>[[datei:Monotonie_quadratfunktion.jpg]]</center>
| + | [[Funktionen_Einstieg/Grenzwert]] |
| | | | |
| − | b) <math>f:x \rightarrow sin(x)</math> in [0;1] <center>[[datei:Montonie_sinusfunktion.jpg]]</center>
| + | [[Funktionen_Einstieg/Symmetrie]] |
| | | | |
| − | c) <math>f:x \rightarrow -\frac{1}{9}x^3 + \frac{1}{2}x^2-1</math> in [0;3] <center>[[datei:Monotonie_kubikfunktion.jpg]]</center
| |
| − |
| |
| − | Was fällt dir auf?
| |
| − | Was haben die drei Funktionsgraphen in den angegebenen Intervallen gemeinsam?
| |
| − | }}
| |
| − |
| |
| − | {{Lösung versteckt|
| |
| − | Alle drei Funktionsgraphen "steigen" in dem angegebenen Intervall an.}}
| |
| − |
| |
| − | Dieser Begriff des Ansteigens eines Funktionsgraphen fassen wir genauer und benennen ihn.
| |
| − |
| |
| − | {{Merke|
| |
| − | Eine Funktion <math> f</math> heißt '''streng monoton zunehmend''' im Intervall [a;b], wenn für alle <math> x_1,x_2 \in [a;b]</math> gilt: <math>x_1 < x_2 \Rightarrow f(x_1) < f(x_2)</math>
| |
| − | }}
| |
| − |
| |
| − |
| |
| − |
| |
| − | {{Arbeiten|NUMMER=2|
| |
| − | ARBEIT=
| |
| − |
| |
| − | Betrachte die folgenden Funktionen in den angegebenen Intervallen Quadratfunktion in den angegebenen Intervallen
| |
| − | </center>
| |
| − | a) <math>f:x \rightarrow x^2</math> in <math>R^-</math> <center>[[datei:Monotonie_quadratfunktion2.jpg]]</center><br>
| |
| − |
| |
| − | b) <math>f:x \rightarrow sin(x)</math> in [2;3] <center>[[datei:Montonie_sinusfunktion.jpg]]</center>
| |
| − |
| |
| − | c) <math>f:x \rightarrow -\frac{1}{9}x^3 + \frac{1}{2}x^2-1</math> in [-3;0] <center>[[datei:Monotonie_kubikfunktion2.jpg]]</center>
| |
| − |
| |
| − | Was stellst du nun fest? Was haben alle drei Graphen in den angegebenen Intervallen gemeinsam?
| |
| − | }}
| |
| − |
| |
| − | {{Lösung versteckt|
| |
| − | Alle drei Funktionsgraphen "fallen" in dem angegebenen Intervall.}}
| |
| − |
| |
| − |
| |
| − |
| |
| − | Auch diesen Begriff des Fallens eines Funktionsgraphen fassen wir - analog zu oben - genauer und benennen ihn.
| |
| − |
| |
| − | {{Merke|
| |
| − | Eine Funktion <math> f</math> heißt '''streng monoton abnehmend''' im Intervall [a;b], wenn für alle <math> x_1,x_2 \in [a;b]</math> gilt: <math>x_1 < x_2 \Rightarrow f(x_1) > f(x_2)</math>
| |
| − | }}
| |
| − |
| |
| − |
| |
| − |
| |
| − | Man könnte diese Begriffe '''monoton zunehmend''' und '''monoton abnehmend''' auch für die Funktionsgraphen übernehmen, hier verwendet man allerdings '''monoton steigend''' und '''monoton fallend'''.
| |
| − |
| |
| − | {{Merke|
| |
| − | Eine Funktionsgraph <math> G_f</math> heißt '''streng monoton steigend''' im Intervall [a;b], wenn die Funktion <math>f</math> dort streng monoton zunehmend ist, <br>
| |
| − | d.h.für alle <math> x_1,x_2 \in [a;b]</math> gilt: <math>x_1 < x_2 \Rightarrow f(x_1) < f(x_2)</math>
| |
| − |
| |
| − | Eine Funktionsgraph <math> G_f</math> heißt '''streng monoton fallend''' im Intervall [a;b], wenn die Funktion <math>f</math> dort streng monoton abnehmend ist, <br>
| |
| − | d.h. für alle <math> x_1,x_2 \in [a;b]</math> gilt: <math>x_1 < x_2 \Rightarrow f(x_1) > f(x_2)</math>
| |
| − | }}
| |
| − |
| |
| − | {{Arbeiten|NUMMER=3|ARBEIT=
| |
| − |
| |
| − | Teste dich! Klicke im folgenden Quiz auf die richtigen Zuordnungen!
| |
| − | }}
| |
| − |
| |
| − | <div class="multiplechoice-quiz">
| |
| − |
| |
| − | [[Bild:Monotonie_f1.jpg|200px]]
| |
| − | (streng monoton steigend) (!streng monoton fallend) (!weder noch)
| |
| − |
| |
| − | [[Bild:Monotonie_f2.jpg|200px]]
| |
| − | (!streng monoton steigend) (streng monoton fallend) (!weder noch)
| |
| − |
| |
| − | [[Bild:Monotonie_f5.jpg|200px]]
| |
| − | (!streng monoton steigend) (!streng monoton fallend) (weder noch)
| |
| − |
| |
| − | [[Bild:Monotonie_f3.jpg|200px]]
| |
| − | (!streng monoton steigend) (streng monoton fallend) (!weder noch)
| |
| − |
| |
| − | [[Bild:Monotonie_f6.jpg|200px]]
| |
| − | (streng monoton steigend) (!streng monoton fallend) (!weder noch)
| |
| − |
| |
| − | [[Bild:Monotonie_f4.jpg|200px]]
| |
| − | (!streng monoton steigend) (!streng monoton fallend) (weder noch)
| |
| − |
| |
| − | [[Bild:Monotonie_f7.jpg|200px]]
| |
| − | (streng monoton steigend) (!streng monoton fallend) (!weder noch)
| |
| − |
| |
| − | </div>
| |
| − |
| |
| − | Für die folgende Multiple-Choice-Aufgabe kannst du als Hilfe GeoGebra öffnen, dir die Graphen der Funktionen zeichnen lassen und dann die Fragen beantworten.
| |
| − |
| |
| − | <div class="multiplechoice-quiz">
| |
| − | <math>f:x \rightarrow x^2</math> im Intervall [2;8]
| |
| − | (streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
| |
| − |
| |
| − | <math>f:x \rightarrow 2sin(x) + 3 </math> im Intervall [<math>\pi;\frac{3}{2}\pi</math>]
| |
| − | (!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch)
| |
| − |
| |
| − | <math>f:x \rightarrow 2^x </math> im Intervall [-1;4]
| |
| − | (streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
| |
| − |
| |
| − | <math>f:x \rightarrow log_2(x) </math> im Intervall [-1;4]
| |
| − | (streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
| |
| − |
| |
| − | <math>f:x \rightarrow 4-x^2 </math> im Intervall [-1;4]
| |
| − | (!streng monoton zunehmend) (!streng monoton abnehmend) (weder noch)
| |
| − |
| |
| − | <math>f:x \rightarrow x^2+2x+1</math> im Intervall [2;8]
| |
| − | (streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
| |
| − |
| |
| − | <math>f:x \rightarrow x^n</math> mit <math> n gerade</math> im Intervall [-4;-1]
| |
| − | (!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch)
| |
| − |
| |
| − | <math>f:x \rightarrow x^n</math> mit <math> n ungerade</math> im Intervall [-3;9]
| |
| − | (streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
| |
| − |
| |
| − | </div>
| |
| | | | |
| | =Grenzwert= | | =Grenzwert= |
Du hast nun Funktionen als Objekte in der Mathematik kennengelernt. Wir wollen als Nächstes untersuchen, welche Eigenschaften Funktionen haben.
Auf den folgenden Seiten sind zum Thema Grenzwert weitere Erklärungen und Beispiele zu finden:
Merke
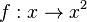
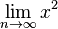
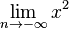
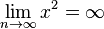und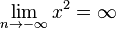 
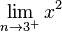heißt: x ist bei der Annäherung größer als 3, also z.B. 3,1 ; 3,01 ; 3,001 usw.
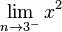heißt: x ist bei der Annäherung kleiner als 3, also z.B. 2,9 ; 2,99 ; 2,999 usw.
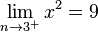bzw.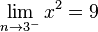 
.
