Wurzelfunktion Einführung: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| − | [[ | + | [[Wurzelfunktion_Startseite|Startseite]] --- [[Wurzelfunktion_Einführung|Die Wurzelfunktion]] - [[Wurzelfunktion_Übungen_1|Übungen]] - [[Wurzelfunktion_Anwendungen|Anwendungen]] - [[Wurzelfunktionen_Eigenschaften|Weitere Eigenschaften]] --- [[Wurzelfunktion_allgemeine_Wurzelfunktion|Die allgemeine Wurzelfunktion]] - [[Wurzelfunktion_Übungen_2|Übungen und Anwendungen]] --- [[Wurzelfunktion_Umkehrfunktion|Die Wurzelfunktion als Umkehrfunktion]] |
---- | ---- | ||
| Zeile 86: | Zeile 86: | ||
---- | ---- | ||
| − | Die Wurzelfunktion hast du nun kennengelernt. Als nächstes kannst du | + | Die Wurzelfunktion hast du nun kennengelernt. Als nächstes kannst du zu [[Wurzelfunktionen_Übungen_1|Übungen]] oder [[Wurzelfunktion_Anwendungen|Anwendungen]] oder [[Wurzelfunktionen_Eigenschaften|Weitere Eigenschaften]] gehen. |
Version vom 30. April 2012, 20:20 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen - Weitere Eigenschaften --- Die allgemeine Wurzelfunktion - Übungen und Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
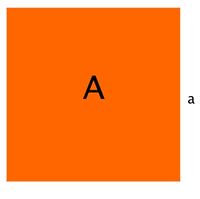
Bei den folgenden Aufgaben bearbeitest du den Zusammenhang zwischen dem Flächeninhalt eines Quadrats und seiner Seitenlänge.
Ein Quadrat mit Seitenlänge  hat den Flächeninhalt
hat den Flächeninhalt 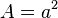 .
.
Ist die Seitenlänge 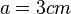 , dann ist also der Flächeninhalt
, dann ist also der Flächeninhalt 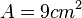 .
.
Umgekehrt ist dann für ein Quadrat mit Flächeninhalt 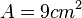 die zugehörige Seitenlänge
die zugehörige Seitenlänge 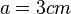 .
.
|
Im folgenden Applet wird der Seitenlänge a) Welcher Flächeninhalt |
Wie kannst du die Seitenlänge eines Quadrats bei gegebenem Flächeninhalt berechnen?
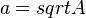
|
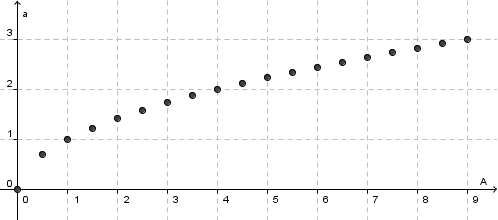
a) Setze in deine Formel verschiedene Werte für A ein und berechne a! Trage die Ergebnisse in eine Wertetabelle ein! b) Stelle deine Wertepaare im Koordinatensystem ( |
In der vorherigen Aufgabe hast du einigen Flächeninhalten exemplarisch ihre Seitenlänge zugeordnet. Mit dem folgenden Applet kannst du diesen Zusammenhang verallgemeinern.
|
a) Verändere mit dem Schieberegler den Wert von |
|
Die Funktion 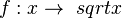 Ihr Graph schaut so aus: 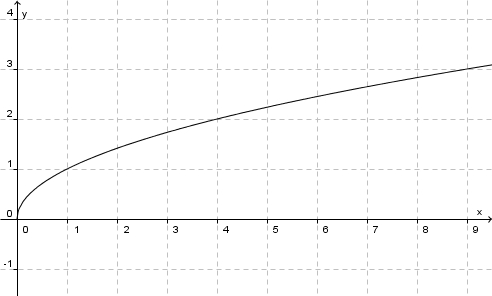
|
|
Gib für die Quadratwurzelfunktion Definitions- und Wertemenge an. |
Aufgabe 1
a) 1; 2,25; 4; 6,25; 9
b) A(a) = a2
c) 25; 100, 225
Aufgabe 2
Aufgabe 3
a) Ja! Jedem Wert 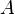 wird genau ein Wert
wird genau ein Wert  zugeordnet.
zugeordnet.
b) Die x-Koordinate des Punktes P ist die Größe A des Flächeninhalts, die y-Koordinate die Länge a der Seite des Quadrats.
c) Die Spur stellt den Graphen der Funktion a mit der Funktionsgleichung 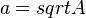 dar.
dar.
Aufgabe 4
Die Wurzelfunktion hast du nun kennengelernt. Als nächstes kannst du zu Übungen oder Anwendungen oder Weitere Eigenschaften gehen.
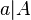 ). Mit dem Schieberegler kannst du verschiedene Werte für
). Mit dem Schieberegler kannst du verschiedene Werte für  , die jeder nicht negativen reellen Zahl x ihre Quadratwurzel
, die jeder nicht negativen reellen Zahl x ihre Quadratwurzel 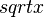 zuordnet heißt Quadratwurzelfunktion oder einfach nur Wurzelfunktion.
zuordnet heißt Quadratwurzelfunktion oder einfach nur Wurzelfunktion.