Wurzelfunktionen Eigenschaften: Unterschied zwischen den Versionen
| Zeile 26: | Zeile 26: | ||
Gib für die folgenden zwei funktionalen Abhängigkeiten | Gib für die folgenden zwei funktionalen Abhängigkeiten | ||
| − | |||
| − | |||
| − | |||
a) Dem Oberflächeninhalt <math>A</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | a) Dem Oberflächeninhalt <math>A</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | ||
b) Dem Volumen <math>V</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | b) Dem Volumen <math>V</math> einer Kugel wird die Länge des Radius <math>r</math> zugeordnet.<br> | ||
| + | |||
| + | # die Funktionsgleichungen an und | ||
| + | # erstelle jeweils eine Wertetabelle und zeichne die Graphen der beiden Funktionen. | ||
| + | |||
}} | }} | ||
| Zeile 36: | Zeile 37: | ||
{{Arbeiten| | {{Arbeiten| | ||
NUMMER=17| ARBEIT= | NUMMER=17| ARBEIT= | ||
| − | |||
| − | + | Verwende die beiden funktionalen Abhängigkeiten aus Aufgabe 16 und | |
| − | + | ||
| − | + | 1. gib die mittlere Änderungsrate für beide Funktionen im Intervall (2;3] an! | |
| − | + | ||
| − | Löse die Aufgabe mithilfe von GeoGebra oder einer Tabellenkalkulation! | + | 2. halte schriftlich fest, welche Bedeutung die mittlere Änderungsrate in diesem Zusammenhang hat! |
| − | + | ||
| − | + | Löse die Aufgabe mithilfe von GeoGebra oder einer Tabellenkalkulation! | |
| + | |||
}} | }} | ||
Version vom 24. Mai 2012, 09:14 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen - Weitere Eigenschaften --- Die allgemeine Wurzelfunktion - Übungen und Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Der Differenzenquotient 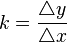 =
= 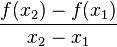 ist der Quotient der Änderung der Funktionswerte y durch die
ist der Quotient der Änderung der Funktionswerte y durch die
Änderung der Abszissenwerte x.
- Er gibt die Steigung einer Sekante durch die Punkte
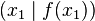 und
und 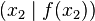 .
.
- Er ermöglicht die Berechnung des Steigungswinkels.
- Er gibt die mittlere Änderungsrate an.
|
Zeichne den Graphen der Funktionen Gib den Steigungswinkel der Sekante an!
|
|
Gib für die folgenden zwei funktionalen Abhängigkeiten a) Dem Oberflächeninhalt
|
|
Verwende die beiden funktionalen Abhängigkeiten aus Aufgabe 16 und 1. gib die mittlere Änderungsrate für beide Funktionen im Intervall (2;3] an! 2. halte schriftlich fest, welche Bedeutung die mittlere Änderungsrate in diesem Zusammenhang hat! Löse die Aufgabe mithilfe von GeoGebra oder einer Tabellenkalkulation! |
Aufgabe 15
Aufgabe 16
Aufgabe 17
Zurück zu Wurzelfunktion oder weiter mit Übungen oder mit Anwendungen.
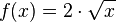 und ermittle die Steigung der Sekante durch die Punkte
und ermittle die Steigung der Sekante durch die Punkte 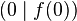 und
und 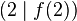 !
!
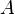 einer Kugel wird die Länge des Radius
einer Kugel wird die Länge des Radius  zugeordnet.
zugeordnet.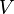 einer Kugel wird die Länge des Radius
einer Kugel wird die Länge des Radius 
