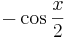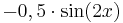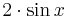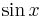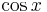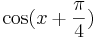Testseite: Unterschied zwischen den Versionen
| Zeile 21: | Zeile 21: | ||
5. Bestimme zu <math>V = \frac{1}{2}V_0</math> die passende Höhe h. | 5. Bestimme zu <math>V = \frac{1}{2}V_0</math> die passende Höhe h. | ||
| + | Im folgenden Applet ist die Füllhöhe h als Funktion des Quotienten <math>\frac{V}{V_0}</math> angegeben. | ||
| + | |||
| + | <ggb_applet width="449" height="525" version="4.0" ggbBase64="UEsDBBQACAAIAOKB2UAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAOKB2UAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vpbb9s4Fn7u/ApCT51FLYsX3Qq7g2bSYAp0bkh3sNiHHdASY7ORJUWSEzuYH7+HpCRLVuvGSZq6NepSFI/O4fnOlXImP62XCboWRSmzdGph27GQSKMslul8aq2qi1Fg/fTqh8lcZHMxKzi6yIolr6YWU5QynlqRQyMm8GxEA+GOmMf5iAduNKIXoXBjPAt4CJRoXcqXafYbX4oy55E4jxZiyd9lEa+04EVV5S/H45ubG7sRZWfFfDyfz+x1GVsItpmWU6u+eAnseg/dUE1OHAeP//PrO8N+JNOy4mkkLKRUWMlXPzyb3Mg0zm7QjYyrBajh+hZaCDlfgE6eSy00VkQ5AJKLqJLXooRHO1Otc7XMLU3GU7X+zFyhpFXHQrG8lrEoppZjE98PwpAy6jIWuH5goayQIq1qWlzLHDfcJtdS3Bi26kpLZBaqsiyZccUR/fMPIg5x0As1YDMQGDzPLDnmnkPNQMzAzOAaGmYeZ4aUGRpmaBjgcC1LOUvE1LrgSQkIyvSiAOu187LaJELvp76x1R6/AJ1KeQvE1AHjG8jhvuO8UF8PvkwtjPtK4o7UqlgdKLQRyVh4d5HkQYrSRiYm/lAmcT+hprdHqNH7LnpitwMtiNL/9Hcgke5Tc1eimT9MoMeeRMXJuAmVSR0dqFwo2tp7KrEsVbzQELmhcnuMXIgNzwcvdxEOYfAJgmhA2EXMhSkOkKdGH1EfFhiiKECKDlOkg8MN4D/ma2YecoGZuutDTCIMghhyKcI6phiCSEI6LiFGCQUK10UuPKTEY6JYUA8xD2Y0QAz2qELSx0BI4UGYg3iCKEZUPYx9RDzkKX6YqVD3ArV1YEmQ5yAPK4YQ1RDRJpqBPkBUaePVcMk0X1U9iKJl3FxWWd7aAqghH22znslPvaT4bJLwmUigTpwrSyJ0zRMVEVrQRZZWqI0Nc29e8Hwho/JcVBU8VaIP/Jq/45VYnwF12cjWtFGWln8UWfVzlqyWaYlQlCVOu+cswZ1r0u4aJrSzwLoLbmfB61z7H5WbwQpalQLkZ0XZkPM4fqsotqkBkPw9TTYnheCXeSb7akzGuuRMxCpKZCx5+hc4q5KicEFtBVLpqqlALPSbjWRFfL4pwYPR+r+iyADHMLDD7gdSzsYsQRVT5biMuIo3FvbpoOBs6iXXsZ3uxzPSxHVrFL4Wrb7zQsbd67flSZbErfZa4Z95Xq0K3S1ANiyUGq/TeSK0U+j8CqU4upxl63PjDdTwer/JYeYY+bO5BhpBMiCuCwT1ODOjplEba6kcTeNoCqdxLxm36zgkmkKPMzNqKvBXs7VaUdxoiZ1GjCx1CnOsXqBoZ59aVxZapbJ6Z2YQNDK6rFXF5oHfVsuZ2PqMIjiVpg0x/VVfDP6omMWjiJmMd1xvcimKVCS1p4PBV9mqNIHbCYJYRHIJU7NQA8eVUf8NezJ3YzEvRE3PE92vGVj1qtN14sFtzeqsyJZv0+v34DE7G5iMm11OyqiQufJLNIPqcCm2vhfLkkNxibvPqdAENCJVRACQSqEFQbuqFlmhWzLINTCqiEzEEhowVGknVD7RIs91Y6cQRtnsA2S7bX0yBB2ggOATHol4ki+4av5qnRO+EUUPBc3u1yzexQag1wpA6OeKgbJ3LoRxlaqOGpQDQx10veQFcJdoPbVGvu1RSCsbuCQ2BNJtdyttCFSQji+h5yx1nLa81cUvMo6FLsUmQVyl5pHSOKFc5omMZFV7mYFzP7Cz7wzYJ8U1ypZLnsYo1Q3U27SC0AcIrW1R547yXcSxQtqAuKqahVPDr+YysJNO5K0dToeG6uUmPRmYSXV8czPMzHBfS23RVo9qH9YXgDUNbBzW9UBvWtWUXuNh7u6knDt6qDguD72PfzaI4RqwUfCY3inWD/FOYbyTD7zzzSHe+eZzRno69xyRBm4P2xjaXIW4SRAP8dCD0BzG+tkhaJ4dD5pPAea5mKv7O1C+MVCeDqCc74eyrLk1WM0/kzi/bPrYIhnUQBLbwwFm1KeeE2L4fOGCpbFLVHZqnRay2bC/vBQiV+3/7+n7gqeleqNoaBpnO9SAp8aAZwMDysMMKI/EgKPvyoJ9zNPVUhQy6hyo9BtPnqwaNOy6wB/agXzKDPiOZqjpykS9t0VLmWo2S77WBbg+rRNlGWUiavu9kzRh2mKB7e4cvS/kunNugaOIvIWjF++pcR87Dhtax71jx9CzzjovQJziU6ObWwhuTq0NmqIA/Qtd/e85RmNEf7R6TdN4fzOVP3IzdaAV97REnk1Z6DmMOH7gEx9sdCQN0tyksXyQxl4fUtJfH09JH2HP9gjDvscCwDwMqbaE69h+6AWUeh4JA6LOU7eman35tik3GMsBxieHYHxyPBh/PYj/yJLNPEt3AH5tAD6BgXysp/pLAr/oEhuy2JDxv9WcQjv7N/6cHYzQBuiW3X1D+OBq376gdIwZXdwxo3uIGT9dJHcbk/h+jcnerT74VM5s7EIaZZg4gc/Ay0xzMiKQYIOQUJfQwMGQYN3HS7BP3Kzs2kH56RFZYljJ6jd+MHcIcWCJgmXUK/fb+i3K92KJ2XFZ4iNNxT5TfFuWOOAMPTyCRYcdwaIjOYI1Sc61CfUI5Def4IAQUocSw3YQOiQMfd9nru8H7Buy527Lj4BV3fNfPL/6cdD2Dzv9i1WqN7I1y7f66vRwg+0/PP1ZA/n86gVSYLaHprqBHGLZ7yz/PJ7OUnUz+n3cMLXddn7JfJRe8qxxqH5W2Tl+qgzjmI4RDxLNYn+iGbjs4qtmmof53Z3BW98RvOJA8IqvG++PHbUf6qhdQ+67Oug1x4f7xetDcSCDY2Bdr5pfykbbs8gX/Fly3P3JXf/BS/23m6/+D1BLBwg2vhCYZQgAAFgqAABQSwECFAAUAAgACADigdlA1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAOKB2UA2vhCYZQgAAFgqAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAA/AgAAAAA" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | |||
| + | 6. Bestimme graphisch und rechnerisch bei welcher Höhe h das eingefüllte Volumen 25%, 40%, 75% des Glasvolumens ist. | ||
}} | }} | ||
| Zeile 38: | Zeile 43: | ||
Ein kegelförmiges Sektglas ist also bei rund 80% der Füllhöhe halb voll. | Ein kegelförmiges Sektglas ist also bei rund 80% der Füllhöhe halb voll. | ||
| + | |||
| + | 6. 5,0 cm; 5,9 cm; 7,3 cm | ||
}} | }} | ||
Version vom 25. Juni 2012, 15:19 Uhr
|
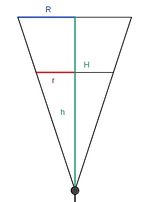
Wann ist ein Sektglas halb voll? Ein Sektglas ist oben kegelförmig. Der Radius R der Deckfläche ist 2,5 cm, die Höhe H des Kegels 8 cm. Bei der Füllhöhe h = 7,639 cm ist das Glas mit 0,2 l gefüllt. (1 l = 1 dm³) Nun interessiert die Frage, wann ist das Glas halb voll? Mit h bezeichnen wir die Füllhöhe. 1. Gib eine Formel für das Volumen mit Füllhöhe h an. 2. Bestimme mit Hilfe des Strahlensatzes einen Zusammenhang zwischen h, H , R und r. 3. Gib nun eine Abhängigkeit des Volumens von h an. 4. Löse dein Ergebnis aus 3. nach h auf. 5. Bestimme zu Im folgenden Applet ist die Füllhöhe h als Funktion des Quotienten
6. Bestimme graphisch und rechnerisch bei welcher Höhe h das eingefüllte Volumen 25%, 40%, 75% des Glasvolumens ist. |
1. 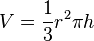
2. 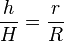
3. Mit 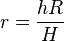 ergibt sich
ergibt sich 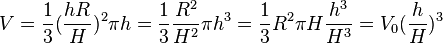 , wobei
, wobei 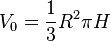 das Glasvolumen ist.
das Glasvolumen ist.
4. Fehler beim Parsen(Syntaxfehler): h = H \sqrt[3]{\frac{V}{V_0}
oder Fehler beim Parsen(Syntaxfehler): h = \sqrt[3]{\frac{3VH^2}{R^2 \pi}
5. ![h = H \sqrt[3]{\frac{1}{2}}=0,7937H\approx 0,8H = 6,4 cm](/images/math/9/2/d/92d01ff2d826057e1ebdc53561882b2a.png)
Ein kegelförmiges Sektglas ist also bei rund 80% der Füllhöhe halb voll.
6. 5,0 cm; 5,9 cm; 7,3 cm
2
4
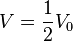 die passende Höhe h.
die passende Höhe h.
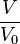 angegeben.
angegeben.
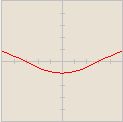
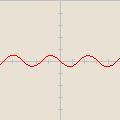
![-\cos [\frac{x}{2}]](/images/math/2/1/2/212d1079c931b2f1abf9a4fc6603a1a1.png)
![-0,5 \cdot \sin [2x]](/images/math/5/8/9/5893264368b318e2deb7f48a7cc94978.png)
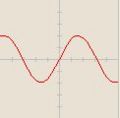
![2 \cdot \sin [x]](/images/math/0/c/8/0c861e4179c5f92a8c48576d0f4477a3.png)
![\cos[x+\frac{\pi}{4}]](/images/math/b/4/e/b4e45ae4dc5d89cbe8a9b9a3366947ea.png)