Quadratische Funktionen 2 - Köln-Arena

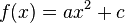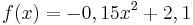
Die Köln-Arena wird von einem parabelförmigen Bogen überspannt. Parabeln kennst du als Graphen quadratischer Funktionen. Hier ist die Parabel allerdings nach unten geöffnet. Finde mit Hilfe des Applets die Parameter a und c zur quadratischen Funktion $f(x) = a x^2 + c$.

[Lösung anzeigen][Lösung ausblenden]

$f(x) = -0,15 x^2 + 2,1$

Du siehst, dass der Koeffizient von $x^2$ auch negativ sein kann. Der Graph ist dann eine nach unten geöffnete Parabel.

Liegt das Bild nicht so im Koordinatensystem, dass der Scheitel auf der y-Achse ist, so kann man trotzdem eine Parabel über den Bogen legen. Es ist ja immer noch das gleiche Bild. Die quadratische Funktion hat dann allerdings die Funktionsgleichung 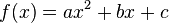$f(x) = a x^2 + bx + c$ mit den Parameter a, b, c.
Finde mit Hilfe des Applets die Werte für a, b und c.

[Lösung anzeigen][Lösung ausblenden]

$f(x) = -0,15 x^2 +1,45x + 0,8$

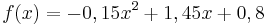
Durch quadratische Ergänzung kannst du den Funktionsterm 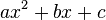$a x^2 + bx + c$ auf die Form 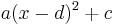$a(x-d)^2 + c$ bringen. Im folgenden Applet ist die quadratische Funktion in dieser Form gegeben. Finde die Parameter a, d, c.

Bei der MediaWiki-Programmerweiterung GeoGebra ist ein Fehler aufgetreten: Ein Parameter wurde nicht angegeben und fehlt daher („width“, „height“ oder „ggbBase64“).

Welchen Einfluss die Parameter a, b und c in der Funktionsgleichung 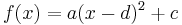$f(x) = a (x - d)^2 + c$ auf den Graphen haben wollen wir als nächstes untersuchen.

Weiter mit Einfluss der Parameter