Quadratische Funktionen 2 Didaktischer Kommentar

Lernpfad Quadratische Funktionen_2 ursprünglicher Lernpfad von © Reinhard Schmidt, Christian Schmidt, Maria Eirich, Andrea Schellmann, überarbeitet von Karl Haberl

Grundsätzliches

Dieser Lernpfad bietet einen Einstieg in das Thema "Quadratische Funktionen". Die Einführung erfolgt am Beispiel des Bremsweges eines Autos, genauer gesagt anhand des Zusammenhangs zwischen der Geschwindigkeit eines Autos und der Länge seines Bremsweges.
Nachdem auf diese Weise der Begriff der reinquadratischen Funktion erarbeitet worden ist, sollen zuerst die Scheitelform einer quadratischen Funktion anhand der Köln-Arena erarbeitet werden.
In der Scheitelform der quadratischen Funktion kommen Parameter vor, deren Einfluss auf den Graphen erkundet wird.
Die Scheitelform einer quadratischen Funktion ist eine allgemeine Beschreibung, die auch in der Form der Funktionegleichung 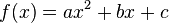$f(x) = a x^2 + bx + c$ beschreibbar ist.
Im Folgenden wird nun diese allgemeine Form der quadratischen Funktion und die Einflüsse der Parameter untersucht. Dieses Themengebiet soll jedoch speziell intuitiv, vor allem durch Experimentieren am Graphen erarbeitet werden.
Der Lernpfad enthält eine Reihe von interaktiven Übungen (Quiz, Memo-Quiz, Multiple-Choice) und GeoGebra- Applets. Dadurch wird den Schülerinnen und Schüler die Gelegenheit gegeben, den funktionalen Zusammenhang zwischen der Geschwindigkeit und dem Brems- bzw. dem Anhalteweg experimentell sowie den Einflüssen der Parameter selbst zu erkunden.
Der Lernpfad ist für 8 Unterrichtsstunden konzipiert und kann im Mathematikunterricht der 9. Jahrgangsstufe eingesetzt werden. Man benötigt dazu internetfähige Rechner, auf denen Java installiert ist.

Lerninhalte und Lernziele

Eingangskompetenzen

Zielkompetenzen • Bei linearen Funktionen zwischen den Darstellungsformen Graph, Tabelle und Formel wechseln • Parameter variieren und die Auswirkung dieser Variation beschreiben (Handhabung von GeoGebra) • von der graphischen Darstellung unmittelbar auf die Darstellung als Formel schließen • Eigenschaften linearer Funktionen aus der Termdarstellung ablesen und sie begründen • Übersetzen von einer Realsituation in ein mathematisches Modell • Parabeln als Graphen quadratischer Funktionen identifizieren • Bei quadratischen Funktionen zwischen den Darstellungsformen Graph, Tabelle und Formel wechseln • Parameter variieren und die Auswirkung dieser Variation beschreiben Lernpfad Quadratische Funktionen

Didaktischer Hintergrund

Intention des Lernpfades ist es, einen motivierenden, zugleich aber auch anspruchsvollen Einstieg in das Thema Quadratische Funktionen anzubieten. Insbesondere soll von vorneherein der Einfluss von Parametern in den Blick genommen werden – im klassischen „Tafelunterricht“ wäre dies an so früher Stelle wohl nur schwerlich möglich. Im kompletten Lernpfad steht die Selbsttätigkeit der Schülerinnen und Schüler im Vordergrund. Im Idealfall muss die Lehrperson nur in Ausnahmefällen in den eigentlichen Lernprozess eingreifen.

Sozialform

Als Sozialform wird für die meisten Teile des Lernpfades Partnerarbeit vorgeschlagen.
Auf diese Weise wird gewährleistet, dass einerseits der zu erarbeitende Stoff selbstständig entdeckt, andererseits aber mit dem Partner argumentiert und kommuniziert wird. Das zu Lernende kann dadurch noch nachhaltiger durchdrungen werden.
Dieser Vorschlag ist jedoch in keiner Weise bindend. Um beispielsweise einen höheren Grad an Selbsttätigkeit zu erzielen, kann auch ein Computer pro Schülerin bzw. pro Schüler veranschlagt werden.

Medien

Der vorliegende Lernpfad wurde bewusst nicht im starren HTML-, sondern im dynamischen Wiki-Format angelegt, damit er beständig optimiert und angepasst werden kann.
Außerdem wurde darauf geachtet, dass die Schülerinnen und Schüler das Thema an Hand von GeoGebra-Dateien experimentell entdecken können.
Interaktive Übungen wie Zuordnungsquiz, Multiple-Choice oder Memo-Quiz erhöhen durch ihren Spiele-Charakter die Motivation.

Sicherung des Gelernten

Da im Lernpfad zunächst reinquadratische, später aber auch allgemeine quadratische Funktionen thematisiert werden, wird die Sicherung des Gelernten an drei Stellen in Form von Übungsseiten in den Lernpfad integriert.
Parallel zur Bearbeitung des Lernpfads empfiehlt sich das Führen eines Lerntagebuchs. Auch die Erstellung eines zusammenfassenden Hefteintrags nach Durcharbeiten des Lernpfads in Partnerarbeit ist eine Möglichkeit zur Sicherung des Gelernten.