Wurzelfunktionen didaktischer Kommentar

Zurück zur Startseite: Wurzelfunktionen

---

Didaktischer Kommentar

Dieser Lernpfad beschäftigt sich mit Wurzelfunktionen und zwar mit

• deren verschiedenen Darstellungsformen (Graph, Tabelle, Formel),
• den Eigenschaften von Wurzelfunktionen (Definitionsmenge, Wertemenge, mittlere Änderungsrate, …),
• den Auswirkungen von Parametervariation,
• der Wurzelfunktion als Umkehrfunktion,
• der Anwendung in verschiedensten Realsituationen.

Mithilfe von dynamischen Arbeitsblättern können experimentell die Eigenschaften von Wurzelfunktionen erarbeitet werden. Viele Anwendungsbeispiele aus unterschiedlichsten Kontexten dienen einerseits der Festigung des Gelernten, zeigen den Schüler/innen aber auch, in welchen Bereichen Wurzelfunktionen benötigt werden (Sichtweite, Bremsweg, Blutvolumen in den Adern,…).

Der Lernpfad unterteilt sich in 7 Phasen, wobei Phase 1 - 4 (beschäftigen sich mit der Quadratwurzelfunktion) auf alle Fälle bearbeitet werden sollen. Phase 5 – 7 können fakultativ bearbeitet werden, da sie als Erweiterung bzw. als Vertiefung dienen. Mögliche Verzweigungen innerhalb des Lernpfads sind am Ende jeder Phase durch Links gekennzeichnet.

Phase 1 (Die Wurzelfunktion):

Das Vorwissen zum Rechnen mit Potenzen kann anhand von drei Übungen aktiviert werden. Dann erarbeiten die Schüler/innen eine formelhafte, tabellarische und graphische Darstellung der Quadratwurzelfunktion und stellen Überlegungen zur Definitionsmenge und Wertemenge an.

Phase 2 (Übungen):

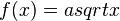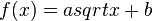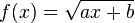Die Inhalte aus Phase 1 können geübt und vertieft werden. Außerdem lernen die Schüler/innen mit Hilfe von Applets die Auswirkun'gen von Parametern in Wurzelfunktion der Form $f(x) = a sqrt x$, $f(x) = a sqrt x + b$ und $f(x) = \sqrt{ax+b}$ kennen.

Phase 3 (Anwendungen):

Drei Beispiele verdeutlichen den Schüler/innen den Einsatz von Wurzelfunktionen in verschiedenen Anwendungssituationen. Das bisher Gelernte wird geübt und weiter vertieft.

Phase 4 (Weitere Eigenschaften):

Der Differenzenquotient mit seinen verschiedenen Verwendungsmöglichkeiten (Steigung der Sekante, Berechnung des Steigungswinkels, mittlere Änderungsrate) wird auf die Wurzelfunktion angewendet.

Phase 5 (Die allgemeine Wurzelfunktion):

Die Schülern/innen erarbeiten eine formelhafte, tabellarische und graphische Darstellung der allgemeinen Wurzelfunktion $f(x) = \sqrt[n]{x}$ und stellen Überlegungen zur Definitionsmenge und Wertemenge an.

Phase 6 (Übungen und Anwendungen): Die bisher kennengelernten Eigenschaften der allgemeinen Wurzelfunktion $f(x) = \sqrt[n]{x}$ werden geübt und in unterschiedlichen Kontexten angewendet.

Phase 7 (Die Wurzelfunktion als Umkehrfunktion):

Der in den Einstiegsbeispielen in Phase 1 und Phase 5 bereits behandelte Zusammenhang zwischen Potenzfunktionen und Wurzelfunktionen wird wieder aufgegriffen und durch Einführung des Begriffs der Umkehrfunktion exaktifiziert. Die Schüler/innen lernen den graphischen Zusammenhang von Funktion und Umkehrfunktionen kennen. Sie lernen das Ermitteln der Funktionsgleichung einer Umkehrfunktion, sowie die Beziehung von Definitionsmenge und Wertemenge von Funktion und Umkehrfunktion kennen.

Kurzinformation

Schulstufe	10. Schulstufe
Dauer	4 - 5 Stunden, es können aber auch einzelne Phasen ausgelassen werden.
Unterrichtsfächer	Mathematik
Verwendete Medien	Java Applets, Internet
Autor/innen	Irma Bierbaumer, Karl Haberl, Evelyn Süss-Stepancik

Voraussetzungen

• Technische Voraussetzungen : Java (kostenlos von www.java.com), Internet
• Technisches Vorwissen: Elementarer Umgang mit dem Computer, Verwendung von dynamischen Applets
• Vorwissen der Schüler/innen: Potenzfunktionen, Rechnen mit Wurzeln, verschiedene Darstellungsformen von Funktionen (Tabelle, Graph, Term).

Lerninhalte und Lernziele

Lerninhalt	Lernziele
Wurzelfunktionen	Wurzelfunktionen definieren, darstellen und untersuchen können. Eigenschaften reeller Funktionen und von Beziehungen zwischen Funktionen (Umkehrfunktionen) beschreiben können. Änderungen durch Änderungsmaße (absolute und relative Änderung, Differenzenquotient) beschreiben können. Funktionen zur Beschreibung kontinuierlicher Prozesse anwenden können.

Genderaspekte

In folgenden Bereichen wurden Genderaspekte berücksichtigt:

Es werden/ es wird

Inhalt und Material

• an den Interessen beider Geschlechter angeknüpft
• geschlechtssensitive bzw. geschlechtsneutrale Bilder verwendet

Genderbewusste Sprache

• eine genderbewusste Sprache in allen Texten und Aufgaben verwendet
• in der Sprache und beim Sprechen beide Geschlechter sichtbar gemacht und / oder geschlechtsneutrale Begriffe verwendet
• weibliche und männliche und / oder geschlechtsneutrale Sprachformen verwendet

Genderansätze in den Lernmaterialien

• interaktive (Experimentier-)Anteile eingesetzt
• kreative Lernfortschrittsüberprüfungen angeboten
• verschiedene Lerntypen angesprochen
• verschiedene Sozialformen eingesetzt
• die mathematischen Inhalte schrittweise exaktifiziert

Kompetenzen

Folgende Handlungsdimensionen kommen im Lernpfad vor:

Darstellen und Modellbilden:

• einen gegebenen mathematischen Sachverhalt in eine andere Darstellungsform übertragen (im gesamten Lernpfad)
• geeignete mathematische Mittel (Begriffe, Modelle, Darstellungsformen, Technologien) und Lösungswege auswählen (im gesamten Lernpfad)
• aus bekannten (z. B. auch elektronisch verfügbaren) mathematischen Modellen neue Modelle entwickeln (im gesamten Lernpfad)
• ein für die Problemstellung geeignetes mathematisches Modell verwenden oder entwickeln (Phase3 – Anwendungen, Phase 6 – Übungen und Anwendungen)

Rechnen und Operieren:

• mit und in Tabellen oder Grafiken operieren (gesamter Lernpfad)
• mit Formeln operieren (gesamter Lernpfad)

Interpretieren:

• Werte aus Tabellen oder grafischen Darstellungen ablesen, sie im jeweiligen Kontext deuten (im gesamten Lernpfad)
• tabellarisch, grafisch oder symbolisch gegebene Zusammenhänge beschreiben und im jeweiligen Kontext deuten (im gesamten Lernpfad)

Argumentieren und Begründen:

• mathematische Zusammenhänge herleiten (im gesamten Lernpfad)

Einsatz im Unterricht

---

Zurück zur Startseite: Wurzelfunktionen