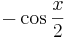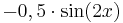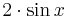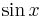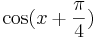Testseite
Aus Medienvielfalt-Wiki
Version vom 25. Juni 2012, 14:26 Uhr von Karlo Haberl (Diskussion | Beiträge)
|
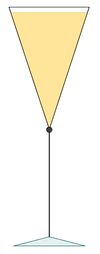
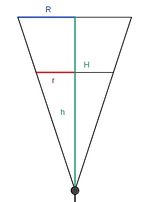
Wann ist ein Sektglas halb voll? Ein Sektglas ist oben kegelförmig. Der Radius R der Deckfläche ist 2,5 cm, die Höhe H des Kegels 8 cm. Bei der Füllhöhe h = 7,639 cm ist das Glas mit 0,2 l gefüllt. (1 l = 1 dm³) Nun interessiert die Frage, wann ist das Glas halb voll? Mit h bezeichnen wir die Füllhöhe. 1. Gib eine Formel für das Volumen mit Füllhöhe h an. 2. Bestimme mit Hilfe des Strahlensatzes einen Zusammenhang zwischen h, H , R und r. 3. Gib nun eine Abhängigkeit des Volumens nur von h an. |
2
4
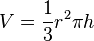
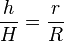
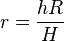 ergibt sich
ergibt sich 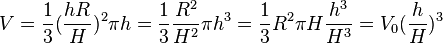
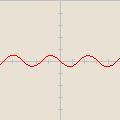
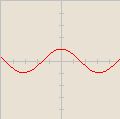
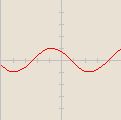
![-\cos [\frac{x}{2}]](/images/math/2/1/2/212d1079c931b2f1abf9a4fc6603a1a1.png)
![-0,5 \cdot \sin [2x]](/images/math/5/8/9/5893264368b318e2deb7f48a7cc94978.png)
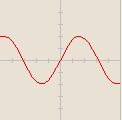
![2 \cdot \sin [x]](/images/math/0/c/8/0c861e4179c5f92a8c48576d0f4477a3.png)
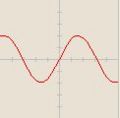
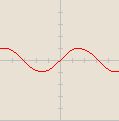
![\cos[x+\frac{\pi}{4}]](/images/math/b/4/e/b4e45ae4dc5d89cbe8a9b9a3366947ea.png)