Wurzelfunktion Einführung: Unterschied zwischen den Versionen
| Zeile 64: | Zeile 64: | ||
{{Merke| | {{Merke| | ||
| − | Die Funktion <math>f</math>, die jeder nicht negativen reellen Zahl x ihre Quadratwurzel <math> sqrt x</math> zuordnet heißt '''Quadratwurzelfunktion''' oder einfach nur '''Wurzelfunktion'''.<br> | + | Die Funktion <math>f</math>, die jeder nicht negativen reellen Zahl x ihre Quadratwurzel <math> \sqrt x</math> zuordnet heißt '''Quadratwurzelfunktion''' oder einfach nur '''Wurzelfunktion'''.<br> |
| − | <center><math> f: x \rightarrow \ sqrt x </math><br></center> | + | <center><math> f: x \rightarrow \sqrt x </math><br></center> |
Ihr Graph schaut so aus:<br> | Ihr Graph schaut so aus:<br> | ||
<center>[[Bild:Graph_quadratwurzelfunktion.jpg]]</center> | <center>[[Bild:Graph_quadratwurzelfunktion.jpg]]</center> | ||
Aktuelle Version vom 27. April 2017, 08:16 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen - Weitere Eigenschaften --- Die allgemeine Wurzelfunktion - Übungen und Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
|
Bei den folgenden Aufgaben bearbeitest du den Zusammenhang zwischen dem Flächeninhalt eines Quadrats und seiner Seitenlänge.
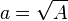
Aufgabe 1 a) 1; 2,25; 4; 6,25; 9 Aufgabe 2 Aufgabe 3 a) Ja! Jedem Wert Aufgabe 4 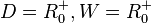 Die Wurzelfunktion hast du nun kennengelernt. Als nächstes kannst du zu Übungen oder Anwendungen oder Weitere Eigenschaften gehen. |
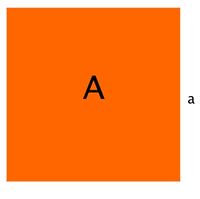
 hat den Flächeninhalt
hat den Flächeninhalt 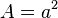 .
.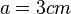 , dann ist also der Flächeninhalt
, dann ist also der Flächeninhalt 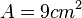 .
. 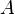 zugeordnet.
zugeordnet. 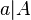 ). Mit dem Schieberegler kannst du verschiedene Werte für
). Mit dem Schieberegler kannst du verschiedene Werte für  , die jeder nicht negativen reellen Zahl x ihre Quadratwurzel
, die jeder nicht negativen reellen Zahl x ihre Quadratwurzel 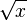 zuordnet heißt Quadratwurzelfunktion oder einfach nur Wurzelfunktion.
zuordnet heißt Quadratwurzelfunktion oder einfach nur Wurzelfunktion.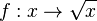
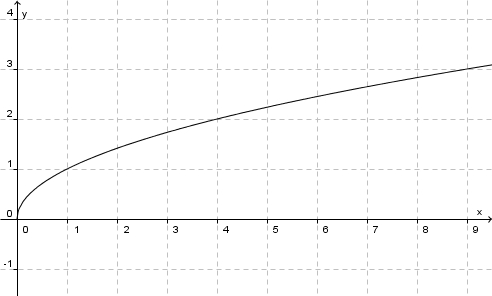
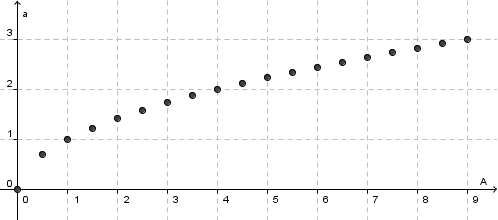
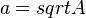 dar.
dar.

