Wurzelfunktion Anwendungen 2: Unterschied zwischen den Versionen
| Zeile 47: | Zeile 47: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
| − | a) <math> T = \sqrt[4]{\frac{P}{A\sigma}}<br> | + | a) <math> T = \sqrt[4]{\frac{P}{A\sigma}}</math><br> |
| − | b) <math>5782 K</math> bzw. <math> | + | b) <math>5782 K</math> bzw. <math>5509^oC</math><br> |
}} | }} | ||
Version vom 3. Februar 2012, 18:00 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen --- Die allgemeine Wurzelfunktion - Übungen - Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
|
Medizinstudenten lernen in der Anfangsvorlesung, dass das Flüssigkeitsvolumen V, das bei konstentem Druck pro Zeiteinheit durch eine Röhre mit Radius r fließt proportional zur 4. Potenz des Radius ist. (Gesetz von Hagen-Poiseuille). Für die Medizinstudenten sind die Röhren Adern im menschlichen Körper und die Flüssigkeit ist Blut. 1. Stelle diesen Sachverhalt als Formel dar. |
1. 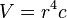 wobei
wobei  eine Konstante ist.
eine Konstante ist.
2. Fehler beim Parsen(Lexikalischer Fehler): r = \sqrt[4]{\frac{V}{c}}\
3. a) Vermehrung um 46%; 506%, 1600%
b) Verminderung um 35%, 93,75%, 100%
4. a) 2,4%
b) 11%
5. a) 2,6%
b) 16%
|
Die zwei österreichischen Physiker Josef Stefan und Ludwig Boltzmann fanden das nach ihnen benannte Strahlungsgesetz. Es besagt, dass die Strahlungsleistung P einer Lichtquelle proportional zur 4. Potenz der Temperatur T dieser Lichtquelle (T gemessen in der absoluten Kelvin-Temperatur) ist. Es ist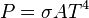 hierbei ist a) Löse die Gleichung nach T auf. |
a) ![T = \sqrt[4]{\frac{P}{A\sigma}}](/images/math/a/6/1/a61d079fa2ed36452b2030f1dfbc9bfe.png)
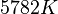 bzw.
bzw. 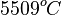
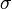 die Stefan-Boltzmann-Konstante
die Stefan-Boltzmann-Konstante 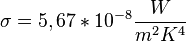 und A die Oberfläche der Lichtquelle.
und A die Oberfläche der Lichtquelle.
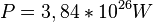 . Wie groß ist die Oberflächentemperatur in K (und in °C) auf der Sonne?
. Wie groß ist die Oberflächentemperatur in K (und in °C) auf der Sonne? 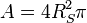 und
der Sonnenradius
und
der Sonnenradius 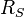 ist circa das 109-fache des Erdradius (6370km).
ist circa das 109-fache des Erdradius (6370km).

