Wurzelfunktion allgemeine Wurzelfunktion: Unterschied zwischen den Versionen
| Zeile 7: | Zeile 7: | ||
| + | Ein Würfel mit der Seitenlänge <math>a</math> hat das Volumen <math> V = a^3</math>.<br> | ||
| + | Ist die Seitenlänge <math>a= 3 cm</math>, dann ist das Volumen <math> V = 27 cm^3</math>. Umgekehrt ist dann für einen Würfel mit Volumen <math> V= 27 cm^3</math> die zugehörige Seitenlänge <math>a= 3 cm</math>.<br> | ||
| + | |||
| + | |||
| + | |||
| + | {{Aufgabe|1= | ||
| + | Im folgenden Applet ist über der Seitenlänge <math>a</math> eines Würfels das Volumen <math>V</math> aufgetragen. Der Punkt V hat die Koordinaten (<math>a, V</math>). Mit dem Schieberegler kannst du verschiedene Werte für a einstellen. | ||
| + | |||
| + | <ggb_applet width="522" height="647" version="4.0" ggbBase64="UEsDBBQACAAIAKZOWUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACACmTllAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1a72/bNhP+3P0VhD5t72pb1C/bhdOhSZqmQLYOSFcM+zCAlmiZtURpIu04xf74HUlJlq24i5J6r5OgKUnxyOM9z93x5Hjy0zpN0IoWgmX8xMJ920KUh1nEeHxiLeWsN7J+ev3dJKZZTKcFQbOsSIk8sTwlySJYQhwSeBHtRREJe97UD3vjIPB6MzsYjgkms3EUWgitBXvFs19ISkVOQnodzmlKrrKQSK14LmX+ajC4ubnpV6r6WREP4njaX4vIQnBMLk6ssvMKtttadONqcce28eD3n6/M9j3GhSQ8pBZSJizZ6+9eTG4Yj7IbdMMiOT+xfBfMmFMWz8Gm4dC30EAJ5QBITkPJVlTA0sZQ2yzT3NJihKv5F6aHktocC0VsxSJanFh23/GdkWvj0QgAcTzftVBWMMplKYtLnYNqt8mK0RuzreppjZ6FZJYlU6J2RH//jRzbsdFL1WDTONAEgZmyzTPbNY1jGs80vpHxzHLPiHpGxjMyHpxxxQSbJvTEmpFEAIKMzwpgrx4LeZtQfZ7ywcZ6/BJsEuwLCLs24Gsgh+e2/VL9BvDrqYnBtpG4oVUWy45KK5W+49xfpfMoQ91KJ3a9tk7H32Nm8BWlxu772In9BrSgSv/Tvy2N7tfM3NVoxo9TGHj/iYmTQRUqkzI6kJgr2dJ7JE2Fihd3jPyxcnuMfIiNYAhe7iM8hmboIIgGhH3k+TDEIxSodojcIUx4yEUjpOSwi3Rw+CP4zxvqzQLkw2bq6RBiEmFQ5CHfRVjHlIcgkpCOS4hRxwUJ30c+LFLqsaO2cAPkBTByR8iDM6qQHGIQdGEhjEG9g1yMXLUYD5EToEDthz0V6sFIHR22dFBgowCrDSGqIaJNNIP8CLnKmqCEi/F8KbcgCtOo6sosr7kAachHm6xn8tNWUnwxSciUJnBPXCsmEVqRREWEVjTLuEQViY55Fhckn7NQXFMpYZVAn8mKXBFJ1xcgLSrdWjbMuPi1yORZlixTLhAKs8Suz5wluNF36lPDwG1MeM0JvzERNPrDO/VmMIOWgoL+rBCVOImi90pikxoAyQ88uT0tKFnkGds2YzLQV86ELsOERYzwT+CsSovCBdU3kEpX1Q0U4HF1kKyIrm8FeDBa/0GLDKAd993mz8hCt2bGHzl9u/EDMyIkKvRcd3vNENbsmXIDo5muaoLImta2x4WK69JuNXgvTrNk80hbf0ZyuSx06QCpsVA2veFxQrWH6GQL93K4mGbr6zJtmr0+3uYwss0BprFGHUFmcHy4kOOynZpWy6iT1VK2lrG1hF35GovqeTx2tIRup6bVUuC85milpbgyE9uVGiZ0PrOtrajRnq9u+SVn8qoaSBYuSkuxkf9lmU7pxn+UwDkzJYmptba14MNpmQx2vHCyoAWnSen0wPcyWwoTw414iGjIUhhuBTdRlP4GZzJPIxoXtJQniS7dDKh61m76c+ux3uqiyNL3fPUR/GXnAJNBdcqJCAuWK7dEU7goFnTjeRETBO6ZqLlORSmgEar7BACRCi2I36WcZ4WuziDtQKuCM6Ep1GJIahfky5QWLKyxJ7rMg0Mty3M7/dIDFfAom36GfLjDlx5oGZje46SIJPmcqOIQl65IbmmxBY3e7ecsKhWXciJRVSVKGdfbpGStQ41MBWRKCWU1UME3ZbU5WJlpoCZRRTuscIKx6t3CWl91ZmzdABQwYl/AJ8iWMZtgkZDFF1CqCh3Rsoxd3blkUUR5fVrCwXs0B5DIcmMugjuEGmevl+Zgvs4aDeZLYloU6URTg/3G+joZDV/ex4ZOLjUf9j35sDtYiO+ysIwJofiwSzZ0+6WRGrSxKlduBaB5uhNMW4it8wL4UccqcTiF17o1nO978hLZP1jbWA7+BeTTh4GsisDYNFPTPBTlDVIq/g6L1FkDKdIVqbPjQ0q3B0HqvELKfgBS58eDVBV93wqpMEtTwiPE9dvONY3Vc2tTfxNb5S1EsIosY+FSVhNTs1u5RwtEUe5WwTR9fP6zD4HhZqsHXBv0L26WCFPnsDRPWMhkDVaicul7LqHqofqOb1cuC0pzVVZ+4B8LwoX62MrIVDdaV8ZODWNnLcbCboyFR8JYbzeVBn3Hf2acnRnOzlucRd04i46EsyrKelWYPUPOzg1nb1qc0W6c0SPhbDfMnlZmbN/6b+v6CP0P2X0f7n7T6VoBvP0/l+4birCKIsWR6RykWLrYwPYjeix0F8dTPLn94cGxe7cHux8fit+7I8TPdA6C3+UdIftg7C6PB7s6br8Zdh0KwYvWBTXrdkHNjuSC6rXTn9vHz66uuDC0vWvRFnejLT4W2nYLi3HfHT430t4Z0i5bpM27kTY/EtJaBfxzJO1y31sX60YaOxLS6vzYe9YJ8mxfgvzcjbbPR0LbHffa03r3ug9pb/cVI4tupC2OhLTdzxF794407D851tqfcSTdWEuOhLU7MuQ9Q+0JstYuRtJurKVHwlqrgnxysdZ+1f3U/Ovdn9+7P3R9vf30L+Tc/df9b/B2i/d9cIj9fvCNPlrZ9vIPhZxnccZJcgVs7zj7J+Pst2/WTLQcnn/d4ZXz1IDxBwH6WGd39lbeuPrLsYH1MN7+ONDXd4KedwA9/w9B/zCbCSoVxkON8OiejBgmGumn/m7NQekYNL8bpL+kV37f/PU/UEsHCOq6RdLQBwAADC8AAFBLAQIUABQACAAIAKZOWUBFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgApk5ZQOq6RdLQBwAADC8AAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAABoCAAAAAA=" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br> | ||
| + | |||
| + | a) Welches Volumen <math>V</math> ergibt sich für <math>a</math> = 1; 1,5; 2; 2,5?<br> | ||
| + | b) Welchen Wert nimmt <math>V</math> für <math>a</math> = 3; 5; 10; 15 an?<br> | ||
| + | c) Lies durch Variation des Schiebereglers ab für welche Werte <math>a</math> das Volumen <math>V</math> = 1,728; 2,744; 3,375; 4,096; 4,913; 9,261; 15,625; 17,576 ist. | ||
| + | |||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | a) a, 3,375; 8; 15,625<br> | ||
| + | b) 27; 125; 1000; 3375<br> | ||
| + | c) 1,2; 1,4; 1,5; 1,6; 1,7; 2,1; 2,5; 2,6 | ||
| + | }} | ||
| − | |||
| − | |||
Es ist | Es ist | ||
Version vom 25. Februar 2012, 09:53 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen --- Die allgemeine Wurzelfunktion - Übungen - Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Ein Würfel mit der Seitenlänge  hat das Volumen
hat das Volumen 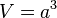 .
.
Ist die Seitenlänge 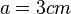 , dann ist das Volumen
, dann ist das Volumen 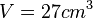 . Umgekehrt ist dann für einen Würfel mit Volumen
. Umgekehrt ist dann für einen Würfel mit Volumen 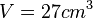 die zugehörige Seitenlänge
die zugehörige Seitenlänge 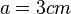 .
.
|
Im folgenden Applet ist über der Seitenlänge
a) Welches Volumen |
a) a, 3,375; 8; 15,625
b) 27; 125; 1000; 3375
c) 1,2; 1,4; 1,5; 1,6; 1,7; 2,1; 2,5; 2,6
Es ist
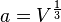
Man schreibt auch dafür
|
Merke:
Die Gleichung 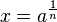 oder Fehler beim Parsen(Lexikalischer Fehler): x = \sqrt[n]{a}\ oder Fehler beim Parsen(Lexikalischer Fehler): x = \sqrt[n]{a}\
Fehler beim Parsen(Lexikalischer Fehler): \sqrt[n]{a}\ heißt die n-te Wurzel aus a. |
|
a) Setze verschiedene Werte für das Würfelvolumen V ein, und berechne welche Werte sich für die Seitenlänge a ergeben. Trage die Ergebnisse in eine Wertetabelle ein. b) Erstelle ein V-a-Diagramm (V nach rechts, a nach oben antragen!) |
|
Merke:
Man definiert für jede natürliche Zahl n die allgemeine Wurzelfunktion n-ten Grades oder n-te Wurzelfunktion Fehler beim Parsen(Lexikalischer Fehler): f: x \rightarrow \sqrt[n]{x}\ mit |
|
Gib für die Würfelaufgabe die zugehörige Funktion an. |
![f:V \rightarrow \sqrt[3]{V}](/images/math/5/6/2/56277ceb06d9f1e85ce77b321e54ee46.png) mit
mit 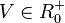
|
1. Stelle mit dem Schieberegler die passende Wurzelfunktion ein.
2. (0;0 und (1;1)
|
Betrachte nun die Wurzelfunktionen im folgenden Applet:
|
- Für ungerade n ist der Funktionsgraph auch für negative x gezeichnet.
- Es ist
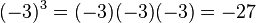 und damit
und damit ![\sqrt[3]{-27}\ = -3](/images/math/7/3/2/7323b20abc6126988a0de2478618344e.png) oder allgemein
oder allgemein 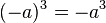 und damit
und damit ![\sqrt[3]{-a^3}\ = -a](/images/math/f/3/8/f389bc623f1322d6697955ebeca3c1d1.png) , also ist bei ungeraden Exponenten n auch die n-te Wurzel aus einer negativen Zahl erklärt.
, also ist bei ungeraden Exponenten n auch die n-te Wurzel aus einer negativen Zahl erklärt.

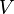 aufgetragen. Der Punkt V hat die Koordinaten (
aufgetragen. Der Punkt V hat die Koordinaten (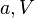 ). Mit dem Schieberegler kannst du verschiedene Werte für a einstellen.
). Mit dem Schieberegler kannst du verschiedene Werte für a einstellen.

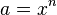 hat für jede natürliche Zahl n und jede nicht negative reelle Zahl x als Lösung
hat für jede natürliche Zahl n und jede nicht negative reelle Zahl x als Lösung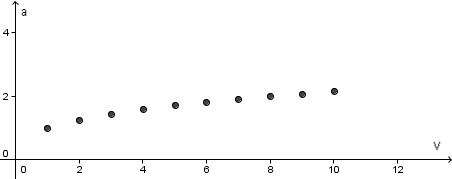
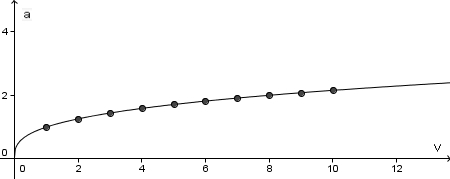
 und
und 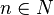 .
.

