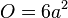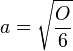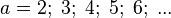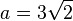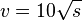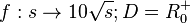Wurzelfunktion Anwendungen: Unterschied zwischen den Versionen
| Zeile 16: | Zeile 16: | ||
}} | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Arbeiten| | {{Arbeiten| | ||
| Zeile 47: | Zeile 41: | ||
# Wie weit kann man von der obersten Plattform des [http://de.wikipedia.org/wiki/Eiffelturm Eiffelturms] (276m), vom [http://de.wikipedia.org/wiki/Mount_Everest Mount Everest] (8848m), von der [http://de.wikipedia.org/wiki/Internationale_Raumstation ISS] (380km) sehen? | # Wie weit kann man von der obersten Plattform des [http://de.wikipedia.org/wiki/Eiffelturm Eiffelturms] (276m), vom [http://de.wikipedia.org/wiki/Mount_Everest Mount Everest] (8848m), von der [http://de.wikipedia.org/wiki/Internationale_Raumstation ISS] (380km) sehen? | ||
# Wie hoch muss ein Berg sein, damit man 100km weit sehen kann? | # Wie hoch muss ein Berg sein, damit man 100km weit sehen kann? | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
}} | }} | ||
| Zeile 70: | Zeile 57: | ||
e) 100m <br> | e) 100m <br> | ||
gemacht hat, gefahren?<br> | gemacht hat, gefahren?<br> | ||
| + | }} | ||
| + | Aufgabe 12 {{Lösung versteckt| | ||
| + | # <math> O = 6 a^2</math> | ||
| + | # <math> a = \sqrt{\frac{O}{6}} </math> | ||
| + | # <math> a = 2;\; 3;\; 4;\; 5;\; 6;\; ...</math> | ||
| + | # <math> a = 3 \sqrt 2</math> | ||
}} | }} | ||
| − | {{Lösung versteckt| | + | Aufgabe 13 {{Lösung versteckt| |
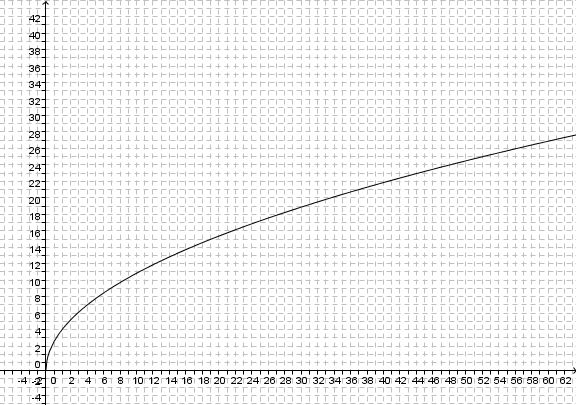
| + | # <br>[[Datei:Wurzelfunktion_3-57.jpg]] | ||
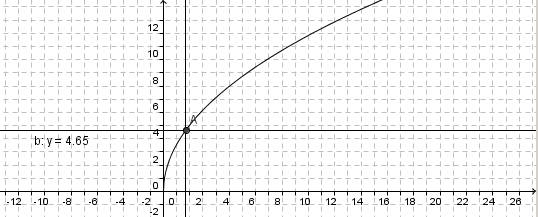
| + | # 4,65km <br>[[Datei:Wurzelfunktion_3-57_2.jpg]] | ||
| + | # 59,3km, 335,8km, 2200km | ||
| + | # 786m | ||
| + | }} | ||
| + | |||
| + | Aufgabe 14 {{Lösung versteckt| | ||
# <math> v = 10 \sqrt s</math> | # <math> v = 10 \sqrt s</math> | ||
# <math> f: s \rightarrow 10 \sqrt s; D = R^+_0</math> | # <math> f: s \rightarrow 10 \sqrt s; D = R^+_0</math> | ||
| Zeile 86: | Zeile 86: | ||
e) 100 <math> \frac{km}{h}</math><br> | e) 100 <math> \frac{km}{h}</math><br> | ||
}} | }} | ||
| − | |||
| − | |||
---- | ---- | ||
Zurück zu [[Wurzelfunktion_Einführung|Wurzelfunktion]] oder weiter mit [[Wurzelfunktionen_Übungen_1|Übungen]]. | Zurück zu [[Wurzelfunktion_Einführung|Wurzelfunktion]] oder weiter mit [[Wurzelfunktionen_Übungen_1|Übungen]]. | ||
Version vom 28. April 2012, 14:40 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen --- Die allgemeine Wurzelfunktion - Übungen - Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Viele Anwendungen der Wurzelfunktion haben einen Faktor a. Daher betrachten wir zuerst die Funktion 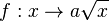 .
.
|
Gib die Funktion, die jeder Oberfläche eines Würfels die Kantenlänge zuordnet als Funktionsterm an.
|
|
Schau dir dieses Video mit Kopfhörern an. Wie weit kannst du bis zum Horizont sehen? Etwa MIt welcher Formel kannst du die Sichtweite a berechnen? Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann bei guten Bedingungen näherungsweise durch die Formel
|
|
Bei den quadratischen Funktionen hast du gelernt, dass der Bremsweg
a) 20m, |
Aufgabe 12 [Lösung anzeigen]
Aufgabe 13 [Lösung anzeigen]
Aufgabe 14 [Lösung anzeigen]
Zurück zu Wurzelfunktion oder weiter mit Übungen.
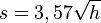 (vgl.
(vgl. 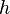 die Augenhöhe in m und
die Augenhöhe in m und  die Sichtweite in km.
die Sichtweite in km.
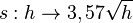 .
.

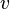 in km/h fährt, mit der Faustregel
in km/h fährt, mit der Faustregel 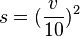 berechnet werden kann.
berechnet werden kann.
 mit Defintionsmenge an, die den Zusammenhang Bremsweg --> Geschwindigkeit beschreibt.
mit Defintionsmenge an, die den Zusammenhang Bremsweg --> Geschwindigkeit beschreibt.