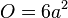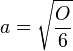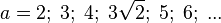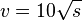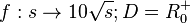Wurzelfunktion Anwendungen: Unterschied zwischen den Versionen
| Zeile 64: | Zeile 64: | ||
# <math> O = 6 a^2</math> | # <math> O = 6 a^2</math> | ||
# <math> a = \sqrt{\frac{O}{6}} </math> | # <math> a = \sqrt{\frac{O}{6}} </math> | ||
| − | # <math> a = 2;\; 3;\; 4;\; 5;\; 6;\; ...</math> | + | # <math> a = 2;\; 3;\; 4;\; 3\sqrt2;\; 5;\; 6;\; ...</math> |
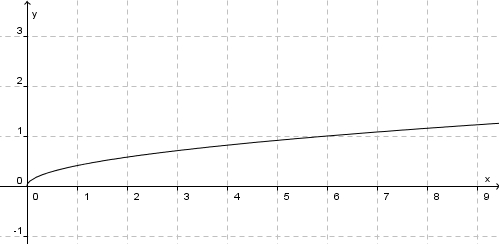
| − | # | + | # [[Datei:WurzelausO6.jpg]] |
}} | }} | ||
Version vom 30. April 2012, 20:11 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen --- Die allgemeine Wurzelfunktion - Übungen - Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
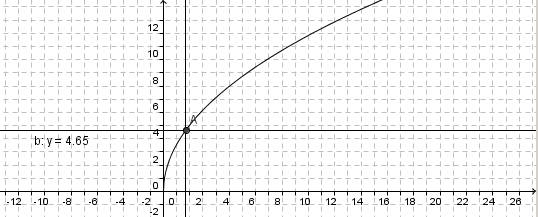
Viele Anwendungen der Wurzelfunktion haben einen Faktor a. Daher betrachten wir zuerst die Funktion 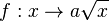 .
.
|
Gib die Funktion, die jeder Oberfläche eines Würfels die Kantenlänge zuordnet als Funktionsterm an.
|
|
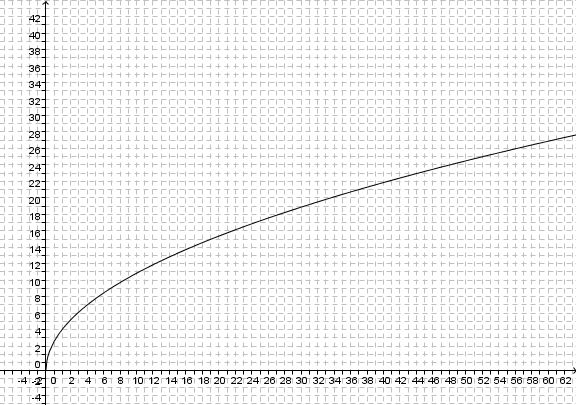
Schau dir dieses Video mit Kopfhörern an. Wie weit kannst du bis zum Horizont sehen? Etwa MIt welcher Formel kannst du die Sichtweite a berechnen? Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann bei guten Bedingungen näherungsweise durch die Formel
|
|
Bei den quadratischen Funktionen hast du gelernt, dass der Bremsweg
a) 20m, |
Aufgabe 12 [Lösung anzeigen]
Aufgabe 13 [Lösung anzeigen]
Aufgabe 14 [Lösung anzeigen]
Zurück zu Wurzelfunktion oder weiter mit Übungen.
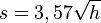 (vgl.
(vgl. 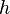 die Augenhöhe in m und
die Augenhöhe in m und  die Sichtweite in km.
die Sichtweite in km.
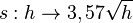 .
.

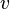 in km/h fährt, mit der Faustregel
in km/h fährt, mit der Faustregel 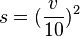 berechnet werden kann.
berechnet werden kann.
 mit Defintionsmenge an, die den Zusammenhang Bremsweg --> Geschwindigkeit beschreibt.
mit Defintionsmenge an, die den Zusammenhang Bremsweg --> Geschwindigkeit beschreibt.