Wurzelfunktion Anwendungen: Unterschied zwischen den Versionen
| Zeile 52: | Zeile 52: | ||
Etwa (!50m) (!500m) (5km) (!50km) | Etwa (!50m) (!500m) (5km) (!50km) | ||
</div> | </div> | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | |||
| + | MIt welcher Formel kannst du die Sichtweite a berechnen? | ||
| + | (<math>a = \sqrt(c^2-b^2)</math> (!<math>a = \sqrt(b^2-c^2)</math>) (!<math>a = \sqrt(a^2-b^2)</math>) (!<math>a = \sqrt(c^2-a^2)</math>) | ||
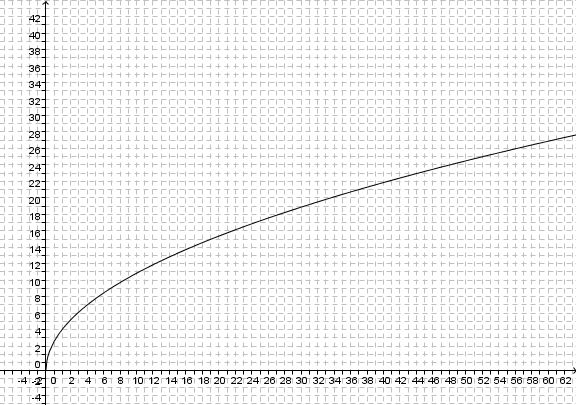
Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann man bei guten Bedingungen durch die Formel <math> s = 3,57 \sqrt h</math> (vgl. [http://de.wikipedia.org/wiki/Sichtweite#Berechnung Sichtweite]) beschreiben. Dabei ist h die Augenhöhe in m und s die Sichtweite in km. Man geht am besten von der Sichtweite auf dem Meer aus, da dort keine Berge stören. Ansonsten nimmt man die "ideale" Kugelgestalt der Erde ohne Berge und Täler. | Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann man bei guten Bedingungen durch die Formel <math> s = 3,57 \sqrt h</math> (vgl. [http://de.wikipedia.org/wiki/Sichtweite#Berechnung Sichtweite]) beschreiben. Dabei ist h die Augenhöhe in m und s die Sichtweite in km. Man geht am besten von der Sichtweite auf dem Meer aus, da dort keine Berge stören. Ansonsten nimmt man die "ideale" Kugelgestalt der Erde ohne Berge und Täler. | ||
Version vom 22. April 2012, 09:23 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen --- Die allgemeine Wurzelfunktion - Übungen - Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Viele Anwendungen der Wurzelfunktion haben einen Faktor a. Daher betrachten wir zuerst die Funktion 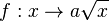 .
.
|
Im Applet ist der Graph der Wurzelfunktion Wie ändert sich der Graph der Wurzelfunktion
|
- Für a = -1 wird der Graph der Wurzelfunktion
 an der x-Achse gespiegelt.
an der x-Achse gespiegelt.
- Für 0 < a < 1 wird der Graph der Wurzelfunktion
 in y-Richtung gestaucht.
in y-Richtung gestaucht.
- Für 1 < a wir der Graph der Wurzelfunktion
 in y-Richtung gestreckt.
in y-Richtung gestreckt.
- Für negative a wird der Graph von 2. oder 3. an der y-Achse gespiegelt.
|
Gib die Funktion, die jeder Oberfläche eines Würfels die Kantenlänge zuordnet als Funktionsterm an.
|
|
Schau dir diesen Video an. Wie weit kannst du bis zum Horizont sehen? Etwa (!50m) (!500m) (5km) (!50km) MIt welcher Formel kannst du die Sichtweite a berechnen?
( Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann man bei guten Bedingungen durch die Formel
|
|
Bei den quadratischen Funktionen hast du kennengelernt, dass der Bremsweg s in m eines Autos, welches mit der Geschwindigkeit v in
a) 20m, |
-
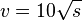
-
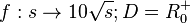
- Für die graphische Lösung kannst du in diesem Applet die entsprechenden Werte mit dem Schieberegler einstellen.
a) 44,7 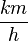
b) 63,2 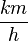
c) 77,5 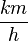
d) 89,4 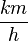
e) 100 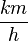
Zurück zu Wurzelfunktion oder weiter mit Übungen.
 dargestellt.
dargestellt.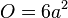
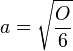
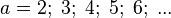
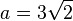
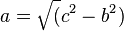 (!
(!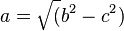 ) (!
) (!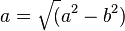 ) (!
) (!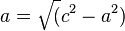 )
)
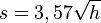 (vgl.
(vgl. 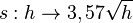 .
.
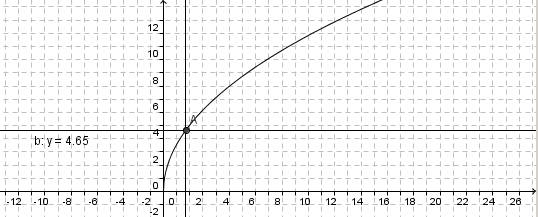

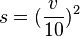 berechnet werden kann.
berechnet werden kann.
 mit Defintionsmenge an, die den Zusammenhang Bremsweg --> Geschwindigkeit beschreibt.
mit Defintionsmenge an, die den Zusammenhang Bremsweg --> Geschwindigkeit beschreibt.

