Wurzelfunktion Umkehrfunktion: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Startseite --- Die Wurzelfunktion - Übungen - [[Wurzelfunktion_Anwendungen|Anwe…“) |
|||
| Zeile 2: | Zeile 2: | ||
---- | ---- | ||
| + | [[Bild:Quadrat.jpg|right]] | ||
| + | |||
| + | |||
| + | |||
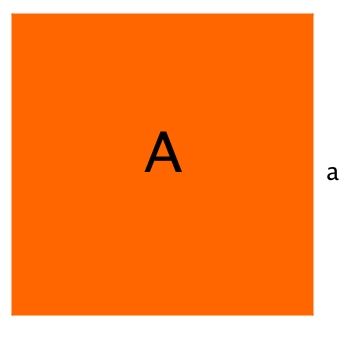
| + | Ein Quadrat mit Seitenlänge a hat den Flächeninhalt <math> A = a^2</math>.<br> | ||
| + | Man weiß von einem Quadrat, dass es den Flächeninhalt 9 FE hat. Wie lang ist dann die Seite? Natürlich 3 LE.<br> | ||
| + | Es ist <math> a = sqrt A</math> | ||
| + | |||
| + | Wie du in diesem Beispeil gesehen hast, erhält man aus dem Flächeninhalt A eines Quadrats die zugehörige Seitenlänge a des Quadrats. | ||
| + | |||
| + | {{Merksatz|MERK= | ||
| + | Ordnet man jeder nicht negativen reellen Zahl x ihre Quadratwurzel zu, so ist die Zuordnung <math> f: x \rightarrow \sqrt x</math> mit <math> x \in R^+_0</math> die Quadratwurzelfunktion oder Wurzelfunktion. | ||
| + | |||
| + | Sie entsteht durch Umkehrung der Fragestellung:<br> | ||
| + | Welchen Flächeninhalt A hat ein Quadrat mit Seitenlänge a?<br> | ||
| + | Diese Fragestellung wird durch die Funktion <math>g:\rightarrow x^2</math> mit <math> x\in R^+_0</math> beschrieben. | ||
| + | |||
| + | Man nennt f die '''Umkehrfunktion''' zur Funktion g. | ||
| + | }} | ||
Version vom 8. Februar 2012, 14:07 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen --- Die allgemeine Wurzelfunktion - Übungen - Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Ein Quadrat mit Seitenlänge a hat den Flächeninhalt 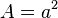 .
.
Man weiß von einem Quadrat, dass es den Flächeninhalt 9 FE hat. Wie lang ist dann die Seite? Natürlich 3 LE.
Es ist 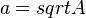
Wie du in diesem Beispeil gesehen hast, erhält man aus dem Flächeninhalt A eines Quadrats die zugehörige Seitenlänge a des Quadrats.
|
Merke:
Ordnet man jeder nicht negativen reellen Zahl x ihre Quadratwurzel zu, so ist die Zuordnung Sie entsteht durch Umkehrung der Fragestellung: Man nennt f die Umkehrfunktion zur Funktion g. |

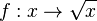 mit
mit  die Quadratwurzelfunktion oder Wurzelfunktion.
die Quadratwurzelfunktion oder Wurzelfunktion.
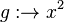 mit
mit 
