Wurzelfunktion Umkehrfunktion: Unterschied zwischen den Versionen
| Zeile 20: | Zeile 20: | ||
Man nennt f die '''Umkehrfunktion''' zur Funktion g. | Man nennt f die '''Umkehrfunktion''' zur Funktion g. | ||
| + | }} | ||
| + | |||
| + | {{Arbeiten|NUMMER=1| ARBEIT= | ||
| + | In diesem Bild sind die Graphen zu den Funktionen <math> f: x \rightarrow \sqrt x</math> mit <math> x \in R^+_0</math> und <math>g:\rightarrow x^2</math> mit <math> x\in R^+_0</math> dargestellt. | ||
| + | |||
| + | <center>[[Datei:Umk_funk_1.jpg]]</center> | ||
| + | |||
| + | Was fällt dir auf? | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | Die Graphen sind zueinander achsensymmetrisch zur Winkelhalbierenden des I. Quadranten | ||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | {{Arbeiten|NUMMER=2| ARBEIT= | ||
| + | Bearbeite diese [http://www.mathe1.de/mathematikbuch/funktionen_umkehrfunktionen_59.htm Seite] | ||
| + | }} | ||
| + | |||
| + | |||
| + | {{Merksatz|MERK= | ||
| + | Für jede natürliche Zahl <math> n </math> ist die Potenzfunktion <math> f: x \rightarrow x^n</math> mit <math> x \in R^+_0</math> umkehrbar.<br> | ||
| + | Die Umkehrfunktion <math> f^{-1}</math> lautet: <math> f^{-1}: x \rightarrow \sqrt[n]{x}</math> mit <math> x \in R^+_0</math>. | ||
}} | }} | ||
Version vom 8. Februar 2012, 14:23 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen --- Die allgemeine Wurzelfunktion - Übungen - Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Ein Quadrat mit Seitenlänge a hat den Flächeninhalt 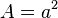 .
.
Man weiß von einem Quadrat, dass es den Flächeninhalt 9 FE hat. Wie lang ist dann die Seite? Natürlich 3 LE.
Es ist 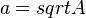
Wie du in diesem Beispeil gesehen hast, erhält man aus dem Flächeninhalt A eines Quadrats die zugehörige Seitenlänge a des Quadrats.
|
Merke:
Ordnet man jeder nicht negativen reellen Zahl x ihre Quadratwurzel zu, so ist die Zuordnung Sie entsteht durch Umkehrung der Fragestellung: Man nennt f die Umkehrfunktion zur Funktion g. |
|
In diesem Bild sind die Graphen zu den Funktionen 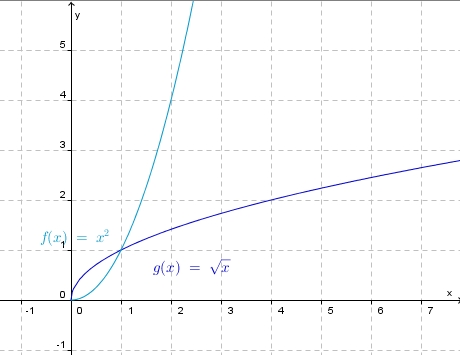 Was fällt dir auf? |
Die Graphen sind zueinander achsensymmetrisch zur Winkelhalbierenden des I. Quadranten
|
Bearbeite diese Seite |
|
Merke:
Für jede natürliche Zahl |

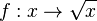 mit
mit  die Quadratwurzelfunktion oder Wurzelfunktion.
die Quadratwurzelfunktion oder Wurzelfunktion.
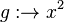 mit
mit 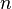 ist die Potenzfunktion
ist die Potenzfunktion 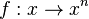 mit
mit 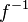 lautet:
lautet: ![f^{-1}: x \rightarrow \sqrt[n]{x}](/images/math/4/3/7/437f5d3ef49490d0b3699c6a229bb421.png) mit
mit 
