Wurzelfunktion Umkehrfunktion: Unterschied zwischen den Versionen
| Zeile 4: | Zeile 4: | ||
[[Bild:Quadrat.jpg|right]] | [[Bild:Quadrat.jpg|right]] | ||
| − | + | Nochmals zum Anfangsbeispiel: | |
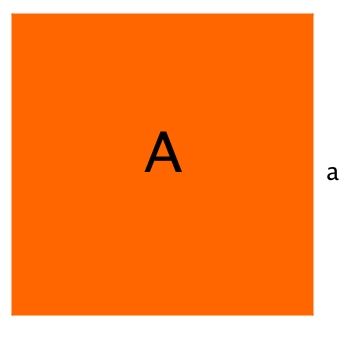
Ein Quadrat mit Seitenlänge a hat den Flächeninhalt <math> A = a^2</math>.<br> | Ein Quadrat mit Seitenlänge a hat den Flächeninhalt <math> A = a^2</math>.<br> | ||
| Zeile 10: | Zeile 10: | ||
Es ist <math> a = sqrt A</math> | Es ist <math> a = sqrt A</math> | ||
| − | + | Ausgangspunkt war die Gleichung <math> A = a^2</math>. Indem man die Gleichung nach <math>a</math> auflöst erhält man sozusagen die Umkehrung. | |
{{Merksatz|MERK= | {{Merksatz|MERK= | ||
| − | |||
| − | + | Ordnet man jeder nicht negativen reellen Zahl <math>x</math> ihr Quadrat <math>x^2</math> zu, so erhält man die Quadratfunktion <math>f:\rightarrow x^2</math> mit <math> x\in R^+_0</math>. | |
| − | + | ||
| − | + | Macht man die Umkehrung umgekehrt und ordnet man jeder nicht negativen reellen Zahl x ihre Quadratwurzel zu, so ist die Zuordnung <math> g: x \rightarrow \sqrt x</math> mit <math> x \in R^+_0</math> die Quadratwurzelfunktion oder Wurzelfunktion. Man erhält diese Funktion durch Umkehrung der Fragestellung:<br> | |
| + | Welche Seitenlänge a hat ein Quadrat mit Flächeninhalt A?<br> | ||
| − | Man nennt | + | Man nennt <math>g</math> die '''Umkehrfunktion''' zur Funktion <math>f</math> und schreibt statt <math>g</math> auch <math> f^{-1}</math>.<br> |
| + | Die Wurzelfunktion <math> f^{-1}: x \rightarrow \sqrt x</math> mit <math> x \in R^+_0</math> ist die Umkehrfunktion zur Quadratfunktion <math>f:\rightarrow x^2</math> mit <math> x\in R^+_0</math>. | ||
}} | }} | ||
| Zeile 25: | Zeile 26: | ||
{{Arbeiten|NUMMER=1| ARBEIT= | {{Arbeiten|NUMMER=1| ARBEIT= | ||
| − | In diesem Bild sind die Graphen zu den Funktionen <math> f: | + | In diesem Bild sind die Graphen zu den Funktionen <math>f:\rightarrow x^2</math> mit <math> x\in R^+_0</math> und <math> g: x \rightarrow \sqrt x</math> mit <math> x \in R^+_0</math> dargestellt. |
<center>[[Datei:Umk_funk_1.jpg]]</center> | <center>[[Datei:Umk_funk_1.jpg]]</center> | ||
| Zeile 43: | Zeile 44: | ||
# graphisch | # graphisch | ||
# rechnerisch<br> | # rechnerisch<br> | ||
| − | von der Potenzfunktion <math> f: x \rightarrow x^n</math> die Umkehrfunktion <math> f^{-1 | + | von der Potenzfunktion <math> f: x \rightarrow x^n</math> die Umkehrfunktion <math> f^{-1}</math>? |
}} | }} | ||
| Zeile 49: | Zeile 50: | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
# Spiegeln an der Geraden <math> y = x</math> | # Spiegeln an der Geraden <math> y = x</math> | ||
| − | # In der Gleichung <math> y = x^n</math> x und y vertauschen und dann nach y auflösen. Man erhält <math> y = \sqrt[n]{x}</math>.<br> | + | # In der Gleichung <math> y = x^n</math> x und y vertauschen und dann nach y auflösen. Man erhält <math> y = \sqrt[n]{x}</math>.<br> Die Umkehrfunktion lautet <math> f^{-1}: x \rightarrow \sqrt[n]{x}</math>. |
Da <math>x \in R^+_0</math> ist, muss man nicht auf die Definitionsmenge aufpassen und diese eventuell einschränken. | Da <math>x \in R^+_0</math> ist, muss man nicht auf die Definitionsmenge aufpassen und diese eventuell einschränken. | ||
}} | }} | ||
Version vom 9. Februar 2012, 07:29 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen --- Die allgemeine Wurzelfunktion - Übungen - Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Nochmals zum Anfangsbeispiel:
Ein Quadrat mit Seitenlänge a hat den Flächeninhalt 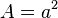 .
.
Man weiß von einem Quadrat, dass es den Flächeninhalt 9 FE hat. Wie lang ist dann die Seite? Natürlich 3 LE.
Es ist 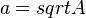
Ausgangspunkt war die Gleichung 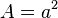 . Indem man die Gleichung nach
. Indem man die Gleichung nach  auflöst erhält man sozusagen die Umkehrung.
auflöst erhält man sozusagen die Umkehrung.
|
Merke:
Ordnet man jeder nicht negativen reellen Zahl Macht man die Umkehrung umgekehrt und ordnet man jeder nicht negativen reellen Zahl x ihre Quadratwurzel zu, so ist die Zuordnung Man nennt |
|
In diesem Bild sind die Graphen zu den Funktionen 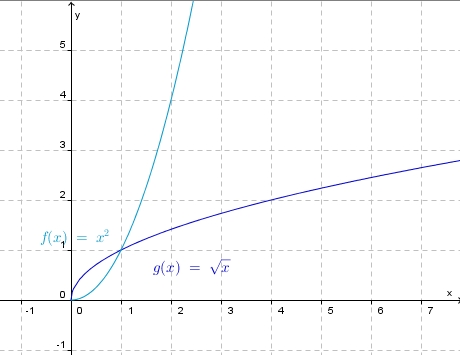 Was fällt dir auf? |
Die Graphen sind zueinander achsensymmetrisch zur Winkelhalbierenden des I. Quadranten
|
Bearbeite diese Seite und beantworte dann:
von der Potenzfunktion |
- Spiegeln an der Geraden
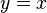
- In der Gleichung
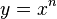 x und y vertauschen und dann nach y auflösen. Man erhält
x und y vertauschen und dann nach y auflösen. Man erhält ![y = \sqrt[n]{x}](/images/math/c/7/b/c7b0045f1674ed5dee699a4a9d3eefef.png) .
.
Die Umkehrfunktion lautet![f^{-1}: x \rightarrow \sqrt[n]{x}](/images/math/4/3/7/437f5d3ef49490d0b3699c6a229bb421.png) .
.
Da  ist, muss man nicht auf die Definitionsmenge aufpassen und diese eventuell einschränken.
ist, muss man nicht auf die Definitionsmenge aufpassen und diese eventuell einschränken.
|
Merke:
Für jede natürliche Zahl |
Bemerkung:
Alle Potenzfunktionen sind für 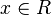 definiert. Dies kann man bei der Bildung von Umkehrfunktionen nicht immer aufrecht erhalten. Potenzfunktionen mit ungeraden Exponenten kann man auch für
definiert. Dies kann man bei der Bildung von Umkehrfunktionen nicht immer aufrecht erhalten. Potenzfunktionen mit ungeraden Exponenten kann man auch für 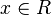 umkehren, bei geraden Exponenten geht dies nicht. Wenn du hierzu mehr wissen willst, lies die folgenden Seite:
umkehren, bei geraden Exponenten geht dies nicht. Wenn du hierzu mehr wissen willst, lies die folgenden Seite:
Potenzfunktionen mit geraden Exponenten haben eine Umkehrrelation
So findet man bei Potenzfunktionen mit geraden Exponenten die Umkehrfunktion

 ihr Quadrat
ihr Quadrat 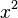 zu, so erhält man die Quadratfunktion
zu, so erhält man die Quadratfunktion 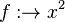 mit
mit 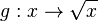 mit
mit 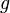 die Umkehrfunktion zur Funktion
die Umkehrfunktion zur Funktion  und schreibt statt
und schreibt statt 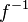 .
.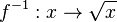 mit
mit 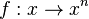 die Umkehrfunktion
die Umkehrfunktion 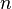 ist die Potenzfunktion
ist die Potenzfunktion 
