Wurzelfunktion Einführung: Unterschied zwischen den Versionen
| Zeile 24: | Zeile 24: | ||
c) Lies durch Variation des Schieberegler ab für welche Werte <math>a</math> der Flächeninhalt <math>A</math> = 1,44; 1, 96; 2,25; 2,56; 3,29; 4,41; 6,25; 7,29; 8,41 ist. | c) Lies durch Variation des Schieberegler ab für welche Werte <math>a</math> der Flächeninhalt <math>A</math> = 1,44; 1, 96; 2,25; 2,56; 3,29; 4,41; 6,25; 7,29; 8,41 ist. | ||
}} | }} | ||
| − | |||
| − | |||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| Zeile 32: | Zeile 30: | ||
c) 1,2; 1,4; 1,5; 1,6; 1,7; 2,1; 2,5; 2,7; 2,9 | c) 1,2; 1,4; 1,5; 1,6; 1,7; 2,1; 2,5; 2,7; 2,9 | ||
}} | }} | ||
| + | |||
| + | |||
Um <math> a </math> aus <math> a </math> zu berechnen, muss man die Wurzel aus <math> A </math> ziehen. | Um <math> a </math> aus <math> a </math> zu berechnen, muss man die Wurzel aus <math> A </math> ziehen. | ||
Version vom 25. Februar 2012, 09:38 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen --- Die allgemeine Wurzelfunktion - Übungen - Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Ein Quadrat mit Seitenlänge  hat den Flächeninhalt
hat den Flächeninhalt 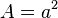 .
.
Ist die Seitenlänge 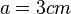 , dann ist der Flächeninhalt
, dann ist der Flächeninhalt 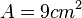 . Umgekehrt ist dann für ein Quadrat mit Flächeninhalt
. Umgekehrt ist dann für ein Quadrat mit Flächeninhalt 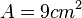 die zugehörige Seitenlänge
die zugehörige Seitenlänge 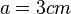 .
.
|
Im folgenden Applet ist über der Seitenlänge
a) Welcher Flächeninhalt |
a) 1; 2,25; 4; 6,25; 9
b) 25; 100, 225
c) 1,2; 1,4; 1,5; 1,6; 1,7; 2,1; 2,5; 2,7; 2,9
Um  aus
aus  zu berechnen, muss man die Wurzel aus
zu berechnen, muss man die Wurzel aus 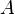 ziehen.
Es ist
ziehen.
Es ist 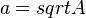
|
a) Setze verschiedene Werte für A ein, und berechnen welcher Wert sich für a ergibt. Trage die Ergebnisse in eine Wertetabelle ein. b) Erstelle ein A-a-Diagramm (A nach rechts, a nach oben antragen!) |
Im folgenden Applet ist ein Quadrat eingezeichnet. Mit dem Schieberegler änderst du den Flächeninhalt und damit die Größe des Quadrats und gleichzeitig trägst du mit dem Punkt P die Seitenlänge über den Flächeninhalt an.
|
a) Variiere mit dem Schieberegler A und verifiziere deine Tabelle. |
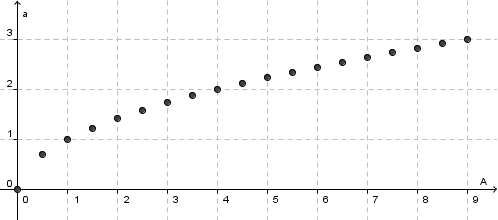
b) Die x-Koordinate des Punktes P ist die Größes A des Flächeninhalts, die y-Koordinate die Länge a der Seite des Quadrats.
c) Über jeden Wert des Flächeninhalts A des Quadrats wird seine Seitenlänge a angetragen. Es ist der Graph der Funktion 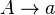 .
.
|
Die Funktion 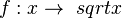 Ihr Graph schaut so aus: 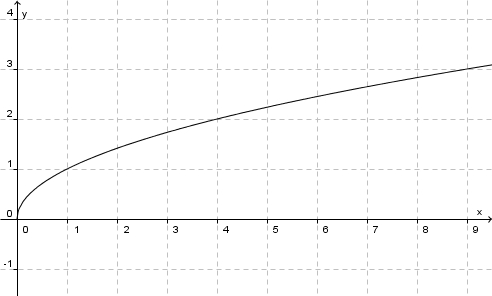
|
Die Wurzelfunktion hast du nun kennengelernt. Als nächstes kannst du wählen, ob du Übungen oder Anwendungen zur Wurzelfunktion behandeln willst.
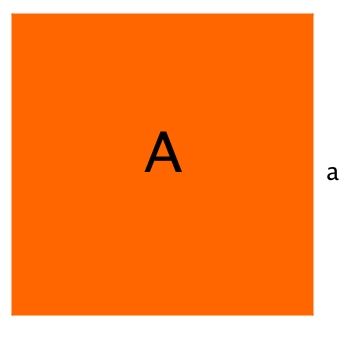
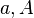 ). Mit dem Schieberegler kannst du verschiedene Werte für a einstellen.
). Mit dem Schieberegler kannst du verschiedene Werte für a einstellen.
 , die jeder nicht negativen reellen Zahl x ihre Quadratwurzel
, die jeder nicht negativen reellen Zahl x ihre Quadratwurzel 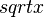 zuordnet heißt Quadratwurzelfunktion oder einfach nur Wurzelfunktion.
zuordnet heißt Quadratwurzelfunktion oder einfach nur Wurzelfunktion.
