Startseite --- Die Wurzelfunktion - Übungen - Anwendungen --- Die allgemeine Wurzelfunktion - Übungen - Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Bei den Übungen zur Wurzelfunktion lernst du weitere sich aus ihr ergebene Funktionen kennen.
Aufgabe 1 
Zeichne den Graphen der Funktionen 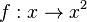 im Intervall [0;3] und den Graphen der Funktion im Intervall [0;3] und den Graphen der Funktion 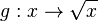 im Intervall [0;7] in ein Koordinatensystem. im Intervall [0;7] in ein Koordinatensystem.
Beschreibe mit Worten die besondere Lage dieser beiden Graphen zueinander.
|
[Lösung anzeigen][Lösung ausblenden]
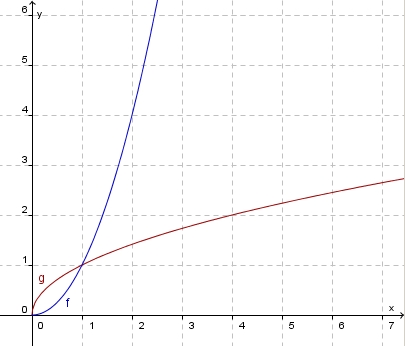
Die Graphen von f und g sind achsensymmetrisch zur Gerade y = x (1. Mediane).
Neben der Quadratwurzelfunktion treten auch Funktionsterme der Art
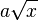 ,
,
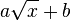 und
und
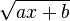
auf. Diese wirst du nun mit dem Gruppenpuzzle untersuchen.
Aufgabe 2 
Im Applet ist der Graph der Wurzelfunktion 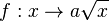 mit mit  dargestellt. dargestellt.
Variiere mit dem Schieberegler den Wert von a.
Wie ändert sich der Graph der Wurzelfunktion  für für
- a = -1
- 0 < a < 1
- 1 < a
- a < 0
|
[Lösung anzeigen][Lösung ausblenden]
- Für a = -1 wird der Graph der Wurzelfunktion
 an der x-Achse gespiegelt.
an der x-Achse gespiegelt.
- Für 0 < a < 1 wird der Graph der Wurzelfunktion
 in y-Richtung gestaucht.
in y-Richtung gestaucht.
- Für 1 < a wir der Graph der Wurzelfunktion
 in y-Richtung gestreckt.
in y-Richtung gestreckt.
- Für negative a wird der Graph von 2. oder 3. an der y-Achse gespiegelt.
[Lösung anzeigen][Lösung ausblenden]
[Lösung anzeigen][Lösung ausblenden]
Aufgabe 4 
Es ist die Funktion 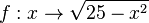 gegeben. gegeben.
- Bestimme die Definitionsmenge.
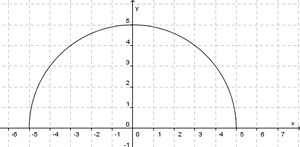
- Zeichne den Graphen.
- Zeige, dass alle Punkte auf dem Graphen vom Ursprung den gleichen Abstand haben.
- Wie kann man den Graphen noch bezeichnen?
|
[Lösung anzeigen][Lösung ausblenden]
-
![D = [-5;5]](/images/math/1/2/0/120287c752ac534bf003f2ea5f8fc0f6.png)
-
- Für einen Punkt P(x;y) auf dem Graphen gilt:
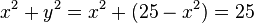 unabhängig von x. Also hat jeder Punkt auf dem Graphen den Abstand 5 vom Ursprung.
unabhängig von x. Also hat jeder Punkt auf dem Graphen den Abstand 5 vom Ursprung.
- Halbkreis
Aufgabe 5 
a) Öffne dieses Arbeitsblatt. Wähle Niveau 2 und finde zum gegebenen Funktionsgraph den passenden Funktionsterm.
Hinweis zur Schreibweise: Schreibe für 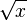 sqrt(x). sqrt(x).
b) Löse dieses Quiz.
|
Zurück zu Wurzelfunktion oder weiter mit Anwendungen
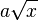 ,
,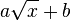 und
und 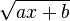
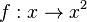 im Intervall [0;3] und den Graphen der Funktion
im Intervall [0;3] und den Graphen der Funktion 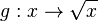 im Intervall [0;7] in ein Koordinatensystem.
im Intervall [0;7] in ein Koordinatensystem.

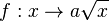 mit
mit  dargestellt.
dargestellt. für
für
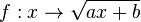 . Im folgenden Applet kannst du mit den Schiebereglern die Werte für
. Im folgenden Applet kannst du mit den Schiebereglern die Werte für  und
und 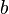 verändern. Anfangs ist
verändern. Anfangs ist 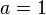 und
und 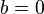 . Es ist der Graph der Quadratwurzelfunktion dargestellt.
. Es ist der Graph der Quadratwurzelfunktion dargestellt.
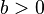 und
und 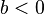 .
.
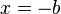 auf. Für
auf. Für 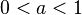 wird der Graph der Wurzelfunktion in y-Richtung gestaucht. Für
wird der Graph der Wurzelfunktion in y-Richtung gestaucht. Für 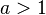 wird der Graph in y-Richtung gestreckt. Ist
wird der Graph in y-Richtung gestreckt. Ist 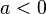 so wird der Graph mit
so wird der Graph mit  an der y-Achse gespiegelt.
an der y-Achse gespiegelt.
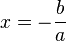
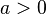 dann ist
dann ist 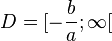 und ist
und ist ![D = ]-\infty;-\frac{b}{a}]](/images/math/2/c/f/2cfe464d0d1d2e691d026209a3879df9.png)
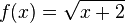
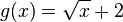
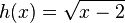
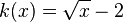
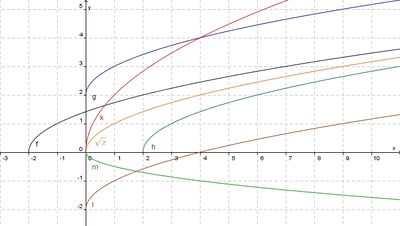
 : Der Graph der Quadratwurzelfunktion wird um 2 nach links verschoben.
: Der Graph der Quadratwurzelfunktion wird um 2 nach links verschoben.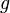 : Der Graph der Quadratwurzelfunktion wird um 2 nach oben verschoben.
: Der Graph der Quadratwurzelfunktion wird um 2 nach oben verschoben.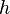 : Der Graph der Quadratwurzelfunktion wird um 2 nach rechts verschoben.
: Der Graph der Quadratwurzelfunktion wird um 2 nach rechts verschoben.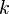 : Der Graph der Quadratwurzelfunktion wird um 2 nach unten verschoben.
: Der Graph der Quadratwurzelfunktion wird um 2 nach unten verschoben.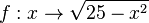 gegeben.
gegeben.
![D = [-5;5]](/images/math/1/2/0/120287c752ac534bf003f2ea5f8fc0f6.png)

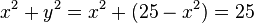 unabhängig von x. Also hat jeder Punkt auf dem Graphen den Abstand 5 vom Ursprung.
unabhängig von x. Also hat jeder Punkt auf dem Graphen den Abstand 5 vom Ursprung.
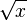 sqrt(x).
sqrt(x).

