Graphen: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
---- | ---- | ||
| − | = | + | =Wiederholung= |
{| width="99%" | {| width="99%" | ||
| style="vertical-align:top" | | | style="vertical-align:top" | | ||
| Zeile 8: | Zeile 8: | ||
<div style="margin: 0; margin-right:10px; border: 0px solid #dfdfdf; padding: 0em 1em 1em 1em; align:left;"> | <div style="margin: 0; margin-right:10px; border: 0px solid #dfdfdf; padding: 0em 1em 1em 1em; align:left;"> | ||
| − | Ein wesentlicher Gesichtspunkt bei Funktionen ist der Funktionsgraph.<br> | + | Ein wesentlicher Gesichtspunkt bei Funktionen ist der Funktionsgraph. Funktionsgraphen hast du schon gezeichnet und sind dir schon bekannt. <br> |
| − | {{ | + | {{Aufgabe| |
| − | + | a) Schaue dir an wie man von der [http://www.juergen-roth.de/dynama/AKGeoGebra/zuordnung_graph/1-f.html Zuordnung zum Funktionsgraph] gelangt. | |
b) Mache die [http://www.juergen-roth.de/dynama/AKGeoGebra/aufgaben_zu_funktionsgraphen/1-f.html Übungen zum Funktionsgraph].<br> | b) Mache die [http://www.juergen-roth.de/dynama/AKGeoGebra/aufgaben_zu_funktionsgraphen/1-f.html Übungen zum Funktionsgraph].<br> | ||
| Zeile 21: | Zeile 21: | ||
| width="50%" style="vertical-align:top" | | | width="50%" style="vertical-align:top" | | ||
<div style="margin:0; border:0px solid #dfdfdf; padding: 0em 1em 1em 1em; align:left;"> | <div style="margin:0; border:0px solid #dfdfdf; padding: 0em 1em 1em 1em; align:left;"> | ||
| + | Verwende Kopfhörer zum Anhören! | ||
{{#ev:youtube |x_vKZ9r8fNs|350}} | {{#ev:youtube |x_vKZ9r8fNs|350}} | ||
| − | |||
</div> | </div> | ||
|} | |} | ||
| − | + | {{Lösung versteckt| | |
| − | + | ||
c) 1. Nach 7 Minuten hat sie 0,525 km zurückgelegt.<br> | c) 1. Nach 7 Minuten hat sie 0,525 km zurückgelegt.<br> | ||
2. Nach 14 Minuten hat sie 1,05 km zurückgelegt.<br> | 2. Nach 14 Minuten hat sie 1,05 km zurückgelegt.<br> | ||
3. Für 400 m braucht sie 5,3 Minuten.<br> | 3. Für 400 m braucht sie 5,3 Minuten.<br> | ||
4. Sie benötigt 13,3 Minuten für 1 km.}} | 4. Sie benötigt 13,3 Minuten für 1 km.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Version vom 1. Juni 2012, 13:48 Uhr
Zuordnungen - Graph und Wertetabelle - Der Funktionsbegriff - Der Funktionsgraph - Beispiele und Übungen - Eigenschaften von Funktionen
Wiederholung
|
Ein wesentlicher Gesichtspunkt bei Funktionen ist der Funktionsgraph. Funktionsgraphen hast du schon gezeichnet und sind dir schon bekannt.
|
Verwende Kopfhörer zum Anhören! |
c) 1. Nach 7 Minuten hat sie 0,525 km zurückgelegt.
2. Nach 14 Minuten hat sie 1,05 km zurückgelegt.
3. Für 400 m braucht sie 5,3 Minuten.
Funktionen grafisch darstellen
Sehr nützlich für die Darstellung von Funktionen ist der Funktionsgraph. Abhängigkeiten zwischen Größen können so auf grafische Weise dargestellt werden. Auch diese Darstellungsform kann mathematisch genau gefasst werden:
 Merke:
 |
Die graphische Darstellung von Funktionen wollen wir nun ein bisschen üben.
Aufgabe 11
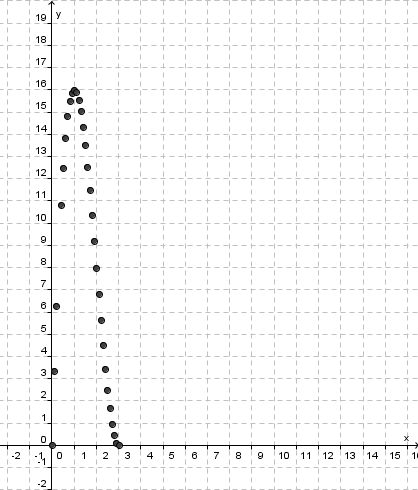
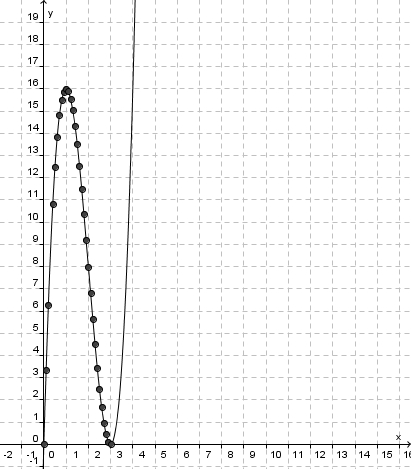
In der Aufgabe Schachtelbeispiel hast du zwei Wertetabellen für den Zusammenhang zwischen V und x erstellt.
(Tipp: Jede Zeile in einer Wertetabelle wird durch einen Punkt in der Zeichenebene dargestellt. Wähle einige beliebige Zeilen einer Wertetabelle aus und zeichne die entsprechenden Punkte in der Ebene ein! Der Graph ist die Menge aller Punkte, die du auf diese Weise einzeichnen könntest: er ist eine Kurve).
|
Aufgabe 12
Auch der Zusammenhang zwischen der Gesprächszeit und der Höhe der Telefonrechnung kann grafisch dargestellt werden. 2. Unser Hotline-Betreuer bekommt einen neuerlichen Anruf: Irene möchte im Monat höchstens 20 € fürs Telefonieren ausgeben. Wie viele Minuten darf sie dann telefonieren? a) Benutze zuerst die von dir erstellte Grafik, um diese Frage zu beantworten! b) Danach benutze die von dir erstellte Wertetabelle, um die Frage zu beantworten! Sind die beiden Antworten gleich? (Und sind sie gleich genau?) Welche Methode fällt dir leichter? |
Graphen können wie oben definiert werden, müssen aber nicht unbedingt der Graph einer Funktion sein. Ein einfaches Erkennungsmerkmal ist:
 Merke
Bei einem Funktionsgraph schneidet jede Parallele zur y-Achse den Graph in höchstens einem Punkt. |
Dies entspricht der Funktionsdefinition, dass jedem Element der Menge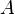 
genau ein Element der Menge 
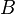zugeordnet wird.
Aufgabe 13
Graph oder nicht Graph Rufe den interaktiven Test Graph oder nicht Graph auf! |
Lösungen:
Aufgabe 11:
Wenn du eine Kurve durch die Punkte legen willst, dann schaut es so aus:
Aufgabe 12:
1. Der Graph ist in diesem Beispiel eine endliche Menge von Punkten in der Zeichenebene, ein so genannter Punktgraph.
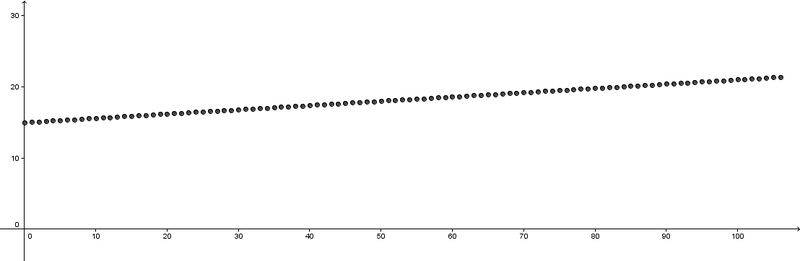
Nun hast du die mathematischen Definitionen für eine Funktion und ihren Graph kennengelernt. Dies wollen wir noch etwas üben.
