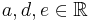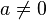Einfluss der Parameter a, d und e in der Scheitelform
Du hast nun den Term 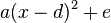 für eine allgemeine quadratische Funktion kennengelernt.
für eine allgemeine quadratische Funktion kennengelernt.
Untersuche nun den Einfluss der Parameter a, d und e bei der quadratischen Funktion  mit
mit 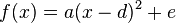
|
Hefteintrag: Am besten verwendest du hierfür dein Heft im Querformat, damit du eine Tabelle mit drei Spalten für den Einfluss von 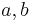 und und  anlegen kannst. Formuliere eine Überschrift und übernimm alle mit gelb gekennzeichneten Texte. Natürlich darfst du dir aber auch noch zusätzlich Notizen machen. anlegen kannst. Formuliere eine Überschrift und übernimm alle mit gelb gekennzeichneten Texte. Natürlich darfst du dir aber auch noch zusätzlich Notizen machen.
|
| Einfluss von a |
Einfluss von d |
Einfluss von e
|
|
Untersuche hier den Einfluss von 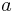
-
auf die Graphen der Funktionen
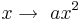 . .
|
Untersuche hier den Einfluss von 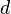
-
auf die Graphen der Funktionen
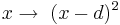 . .
|
Untersuche hier den Einfluss von 
-
auf die Graphen der Funktionen
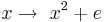 . .
|
|
|
Du hast eine Menge über den Einfluss der einzelnen Parameter auf das Aussehen der Graphen herausgefunden. Natürlich können aber die Parameter nicht nur einzeln variiert werden, sondern auch mehrere oder alle gleichzeitig.
|
Merke:
Die Scheitelform der quadratische Funktion lautet
-
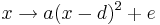 . .
Dabei sind 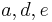 Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Es gilt Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Es gilt 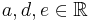 und und 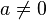 . .
- Der Scheitel hat die Koordinaten (d;e).
|
|
Verdeutliche dir mit diesem Applet noch einmal die Wirkung der einzelnen Parameter und beachte die Identitäten in Term und Scheitelkoordinaten.
Bestimme die Parameter a, d und e
|
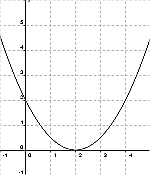
[Lösung anzeigen][Lösung ausblenden]
- Der Scheitel hat die Koordinaten (2;0).
- Also gilt d = 2, e = 0.
- Der Punkt (0;2) liegt auf der Parabel.
- Es gilt 2 = a(0 - 2)2.
- Damit ist a = 0,5.
|
|
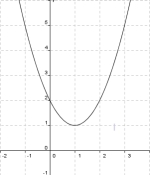
[Lösung anzeigen][Lösung ausblenden]
- Der Scheitel hat die Koordinaten(1;1).
- Also ist d = 1 und e = 1.
- Der Punkt (0/2) liegt auf der Parabel
- Es gilt also 2 = a·(0 - 1)2 + 1.
- Damit ist a = 1.
|
|
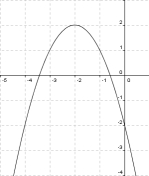
[Lösung anzeigen][Lösung ausblenden]
- Der Scheitel hat die Koordinaten(-2;2).
- Also ist d = -2 und e = 2.
- Der Punkt (-1/1) liegt auf der Parabel
- Es gilt also 1 = a·(-1 + 2)2 + 2.
- Damit ist a = -1.
|
|
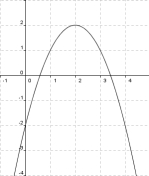
[Lösung anzeigen][Lösung ausblenden]
- Der Scheitel hat die Koordinaten(2;2).
- Also ist d = 2 und e = 2.
- Der Punkt (1/1) liegt auf der Parabel
- Es gilt also 1 = a·(1 - 2)2 + 2.
- Damit ist a = -1.
|
|
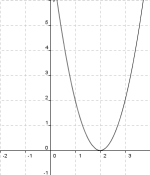
[Lösung anzeigen][Lösung ausblenden]
- Der Scheitel hat die Koordinaten(2;0).
- Also ist d = 2 und e = 0.
- Der Punkt (1/2) liegt auf der Parabel
- Es gilt also 2 = a·(1 - 2)2.
- Damit ist a = 2.
|
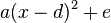 für eine allgemeine quadratische Funktion kennengelernt.
für eine allgemeine quadratische Funktion kennengelernt.
 mit
mit 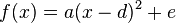

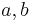 und
und  anlegen kannst. Formuliere eine Überschrift und übernimm alle mit gelb gekennzeichneten Texte. Natürlich darfst du dir aber auch noch zusätzlich Notizen machen.
anlegen kannst. Formuliere eine Überschrift und übernimm alle mit gelb gekennzeichneten Texte. Natürlich darfst du dir aber auch noch zusätzlich Notizen machen.
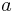
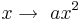 .
.
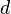
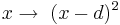 .
.

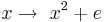 .
.
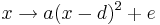
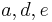 Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Es gilt
Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Es gilt